Matykání: výchova trojúhelníků v Čechách

V předchozích dílech jsme na několika příkladech viděli, že zatímco v hyperbolické geometrii jsou úhly v trojúhelníku trochu podvyživené, ve sférické geometrii jsou naopak nadvyživené. Dnes se tomuto fenoménu podíváme na zoubky.

V eukleidovské geometrii panuje krutopřísný režim. Disciplinované trojúhelníky mají na úhlech přesně 180°, ať jsou velké nebo malé, tlusté nebo hubené, ostroúhlé nebo tupoúhlé. Tomu říkám slušně vychované polygóny, pane vašnosto.

Jakmile ale trojúhelníky vypustíte na křivočarou pastvinu, začnou s nimi šít čerti. Vyškrábou se na sféru a součet úhlů se jim rázem zvětší nad 180°, protože strany trojúhelníka budou trochu "vypouklé" (dá se ale ukázat, že součet úhlů bude stále menší než 540°). Vyhoupnou se do hyperbolického sedla a součet úhlů bude najednou menší než 180° a limitně se bude blížit 0°, pokud se všechny tři vrcholy trojúhelníku nastěhují k hranici (tj. k ose x v modelu poloroviny a k jednotkové kružnici v kruhovém modelu).

Na první pohled by se mohlo zdát, že v rámci takto vymezených mantinelů si trojúhelníky mohou dělat víceméně co se jim zlíbí, ale není tomu tak. O jejich výchovu se stará jedna klasická věta z diferenciální geometrie.

Nejprve si ale zadefinujeme kvantitu, která nám prozradí, jak moc je daný trojúhelník nezbedný - tedy o kolik se součet jeho vnitřních úhlů liší od 180°. Ten úhlový přebytek (ve sférickém případě), respektive nedostatek (v případě hyperbolickém) se zove úhlový defekt a řídí se velmi přesnými zákony.

Označíme-li si součet vnitřních úhlů písmenkem ?=? + ß + ?, pak úhlový defekt ? definujeme jako

? = ? - 180°  (respektive ? = ? - ? měříme-li úhly v radiánech)

Velikost úhlového defektu závisí na geometrii variety, ve které se trojúhelník nalézá, a spočítá se z tzv. Gauss-Bonnetovy věty, která se obecně zabývá vztahem mezi křivostí plochy a její topologií. Pro naši potřebu ale bude stačit speciální případ. Zhruba řečeno platí, že defekt je roven akumulované hodnotě křivosti K uvnitř trojúhelníku T a tu vyjádříme spojitým součtem - tedy integrálem přes T:

? = ?K

Pokud je křivost plochy K=k konstantní, pak se formulka zjednodušší - křivost vytkneme a zůstane nám tam integrál z jedničky, což je velikost množiny přes kterou integrujeme - takže akumulovaná křivost bude k krát plocha P daného trojúhelníku:

? = k.P

Konkretně pro eukleidovskou geometrii je křivost k=0, takže defekt je 0 a všechny trojúhelníky mají očekávaných 180° (přestože pro názornost používám stupně, ve formulkách pro defekt je nutno měřit úhly v radiánech).

Ve sférické geometrii je křivost kladná a při vhodné volbě jednotek je k = 1, takže úhlový defekt (zde přebytek) bude přesně roven ploše trojúhelníku. To mimochodem znamená, že velmi malé trojúhelníky budou mít malý defekt a budou se chovat podobně jako trojúhelníky eukleidovské, což odpovídá intuitivní představě, že velmi malý trojúhelníček nemá dostatek prostoru, aby se mohl zakřivit (z jeho pohledu je sféra příliš velká) a chová se tedy lokálně stejně jako v eukleidovské rovině (trojúhelník narýsovaný v Polabí prakticky nerozeznáte od jeho eukleidovského protějšku, přestože leží na sféře).

V hyperbolické geometrii je situace analogická s opačným znaménkem. Gaussova křivost je záporná a ve vhodně vybraných jednotkách bude k=-1, takže úhlový defekt bude mínus plocha trojúhelníku. O tuto hodnotu bude součet úhlů "pod míru". A ze stejného důvodu bude pro malé trojúhelníky situace téměř eukleidovská - tj. trojúhelníky budou mít jen nepatrně pod 180°.

V první sekci se dnes podíváme podrobněji na sférický případ. Ve druhé na hyperbolický a ve třetí na jednu praktickou aplikaci.

+++++++++

Defekt sférických trojúhelníků

Rychloopáčko: roli přímek hrají na sféře tzv. velké kružnice, což jsou průsečíky sféry a libovolné roviny procházející počátkem. To jsou křivky, podél kterých létají letadla.

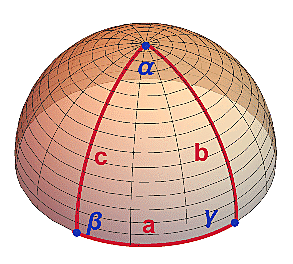
Abychom do sférické geometrie vpluli pomalu, podíváme se opět nejprve na speciální případ, kdy bude trojúhelník tvořen rovníkem a dvěma poledníky. Oba úhly na rovníku jsou pravé (tedy 90°), zatímco úhel ? na pólu může mít libovolnou hodnotu (obrázek vpravo).

Pokud je úhel ? malý - tj. poledníky běží těsně vedle sebe - bude součet úhlů jen o něco vyšší než 180°. Jak ale začneme obě poledníková ramena b a c rozšiřovat, úhel ? se bude zvětšovat a v principu ho můžeme dotáhnout až do hodnoty ?=360°, pokud ramena "odstrčíme" až na druhou stranu - a v tomto případě se součet úhlů ? bude blížit až k hodnotě 540° (defekt pak bude ?=360°).

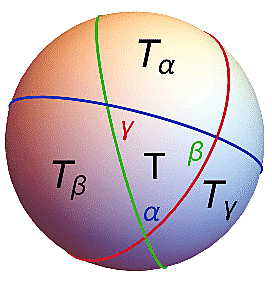
Zdaleka ne každá velká kružnice je ale rovníkem nebo poledníkem. Proto si pro výpočet defektu musíme nabrnkat obecný trojúhelník a provést všechny úvahy v něm (další obrázek). Vezmeme si tedy trojúhelník T na jednotkové sféře omezený třemi obecnými, libovolně zvolenými velkými kružnicemi - modrou, červenou a zelenou.

Tyto tři velké kružnice (geodetiky) rozbijí sféru na 8 malých trojúhelníkových území. Jednak trojúhelník T (s vnitřními úhly ?, ß a ?), pak tři přilehlé oblasti T?, Tß a T?, omezené každým ze tří možných párů velkých kružnic a konečně symetrické protějšky těchto území. Na "odvrácené" straně sféry se nalézá trojúhelník T' (tvořený protilehlými body trojúhelníku T) a pak tři symetrické oblasti T'?, T'ß a T'? (jejichž "ocásky" lze vidět na obrázku). Pokud vám to rozdělení "neštymuje", tak si ty tři kružnice nakreslete na tenisák a uvidíte to v cuku letu.

Základem výpočtu je skutečnost, že trojúhelník T a jedna každá z těch přilehlých oblastí, řekněme T?, tvoří zvláštní množinu, které se říká sférická luna. Dvě velké kružnice se protínají ve dvou protilehlých bodech, které si můžeme představit jako severní a jižní pól. Klasickými lunami jsou pak oblasti mezi poledníky od severního k jižnímu pólu (mimochodem, existují machři, kteří dokáží oloupat pomeranč na luny).

Některé luny jsou užší a některé širší, podle úhlu sevřeného na severním a jižním pólu. Plocha každé luny je tomuto úhlu úměrná. Je-li tedy úhel dané luny ? (v radiánech!), bude její plocha rovna ploše celé sféry (což je 4? r2), krát konstanta úměrnosti (což je poměr mezi úhlem luny a plným úhlem - tedy ?/2?), takže nám pro plochu vyjde P(luna)=2?r2. A protože budeme pracovat s jednotkovou sférou (r=1), plocha luny odpovídající úhlu ? bude P=2?.

No a začneme počítat.

Celková plocha jednotkové sféry je P = 4?.

Trojúhelníky T, T?, Tß a T? zaberou přesně polovinu sféry, protože jsou stejně velké jako jejich symetrické protějšky T', T'?, T'ß a T'? a všechny dohromady zaplní celou sféru. Takže

P(T) + P(T?) + P(Tß) + P(T?) = 2?

Současně ale dostaneme rovnice pro tři luny, vytvořené tak, že k trojúhelníku T přidáme postupně tři přilehlé trojúhelníky T?, Tß a T?. A plochu lun spočítáme z jejich úhlů.

P(T) + P(T?) = 2?
P(T) + P(Tß) = 2ß
P(T) + P(T?) = 2?

Sečtením těchto rovnic dostaneme

3P(T) + P(T?) + P(Tß) + P(T?) = 2(?+ß+?)

a odečteme-li předchozí rovnici od této, dostaneme

2P(T) = 2(?+ß+?-?)

a po vydělení 2 dostaneme přesně vzoreček, který jsme chtěli: plocha trojúhelníku se rovná úhlovému defektu.

A ani jsme nepotřebovali žádný sofistikovaný aparát.

+++++++++

Defekt hyperbolických trojúhelníků

Rychloopáčko: v Poincarého modelu bude naším hyperbolickým pískovištěm horní polorovina (x>0), ve které roli přímek převezmou kružnice kolmé na osu x (včetně svislých přímek, na které pohlížíme jako na kružnice s nekonečným poloměrem)

V hyperbolickém případě si na výpočet plochy trojúhelníku a úhlového defektu budeme muset přizvat integrální počet. Ale není důvod panikařit. Integrál není nic jiného než spojitý součet, takže do sebe kopněte panáka a jdeme na věc.

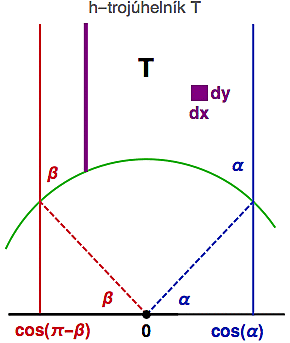
Nejprve se podíváme na velice speciální typ trojúhelníku, který má jeden z vrcholů v nekonečnu (tedy vysoko převysoko nad osou x). Bude to trojúhelník na obrázku vpravo omezený modrou, červenou a zelenou hyperbolickou přímkou. Ta zelená bude pro jednoduchost jednotková kružnice (pro obecnou kružnici se výpočet provede analogicky, jen bude trochu techničtější).

Jeden z jeho úhlů (ten v nekonečnu) je nula, protože dvě z jeho hraničních přímek (modrá a červená) jsou rovnoběžné. Zbývající dva úhly si označíme ? a ß. Díky tomu, že poloměr kružnice je kolmý na její tečnu dostaneme stejné úhly ještě v počátku a z nich si lehce spočítáme (zelená kružnice je jednotková) polohu červené a modré přímky.

Plochu trojúhelníku T spočítáme tím nejdrsnějším možným způsobem. Pokryjeme ho malými infinitesimálními (fialovými) čtverečky o stranách dx a dy, spočítáme jejich plošky a nakonec je všechny posčítáme. Protože ty čtverečky jsou ale nekonečně malé, budeme to muset udělat ne součtem, ale integrálem.

Nejprve si připomeneme, že v Poincarého polorovině se měří infinitesimální rozměry tak, že běžné eukleidovské rozměry se vydělí y souřadnicí místa, kde měření provádíme. A to platí jak pro šířku dx, tak pro výšku dy. Zatímco v eukleidovské geometrii by měl ten jeden fialový infinitesimální čtvereček obsah dx*dy, v hyperbolické bude mít obsah

(dx/y)*(dy/y) = dx*dy/y2

No a můžeme začít sčítat (ten integrální klikyhák si klidně představte jako sčítací symbol)

P = ??dx*dy/y2

(sčítací symboly tu jsou dva, protože musíme sečíst přes y a pak přes x)

P = ? (?dy/y2) dx

Ten integrál v závorce (pro pevně zvolené x) v podstatě sčítá ty čtverečky podél svislé fialové čáry tímto x určené. Výsledek tohoto vnitřního součtu bude samozřejmě na x záviset a proto nakonec musíme ještě provést vnější součet, kde ty "svislé" mezisoučty posčítáme přes x.

Každý z těch integrálů má určité meze, které integrálnímu počtu říkají odkud kam chceme daný výraz sčítat (integrovat).

V našem případě ten vnitřní součet (integrál) bude sčítat od hodnoty y=sqrt(1-x2), což je bod jednotkové kružnice určený danou hodnotou x, až nahoru do nekonečna y=?. Vnější součet pak všechny ty dílčí mezisoučty posčítá od červené přímky až po tu modrou. Tedy od hodnoty x=cos(?-ß) až do x=cos(?).

A jak to vyčíslit? Ten vnitřní integrál je celkem jednoduchá funkce jedné proměnné, jejíž integrál si lehce najdeme v tabulkách

?dy/y2 = -1/y

a musíme do něho dosadit obě meze a odečíst. Hodnota té funkce vpravo je pro y=? rovna 0, takže z toho vnitřního integrálu nám zůstane pouze první hodnota y: 1/sqrt(1-x2). A protože ji odečítáme, to mínusko z předchozí formulky se vyruší. A teď se soustředíme na vnější integrál.

P = ? (1/sqrt(1-x2)) dx

Protože ten výraz v závorce je derivace funkce arcsin(x), respektive -arccos(x), i tento integrál se vyčíslí celkem lehce (nebo si ho najdete v tabulkách) jako

P = [-arccos(x)]

kde hranatá závorka značí, že do funkci uvnitř musíme dosadit obě hraniční hodnoty a odečíst (při tom nám ten arccos sežere oba kosíny, takže dostaneme pouze čisté úhly)

(+) P = -arccos(cos(?)) - (-arccos(cos(?-ß)) = (?-ß)-? = ?-?-ß

No a je to. Náš speciální trojúhelník (s jedním vrcholem v nekonečnu) má plochu ?-?-ß.

Dál už to bude procházka růžovým sadem.

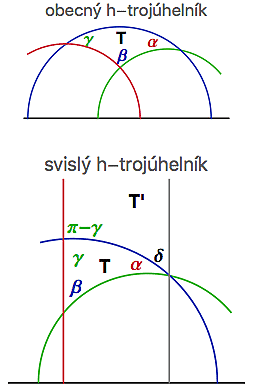
Obecný trojúhelník T (obrázek nahoře) nejprve natočíme tak, aby jedna jeho strana byla svislá. To by se v eukleidovském případě hravě provedlo tak, že bychom trojúhelník prostě pootočili vhodně zvolenou rotací. V hyperbolickém případě je nutno místo rotace použít jednu z těch Möbiových transformací, které jsme probírali minule, ale výsledek je stejný. Dostaneme kongruentní trojúhelník (se stejnými stranami a úhly), jehož jedna strana bude svislá (obrázek dole).

A protože jsme se právě s jazykem na vestě naučili počítat plochy trojúhelníků, jejichž dvě strany jsou svislé, narýsujeme si v průsečíku modré a zelené hyperbolické přímky ještě šedou svislou přímku, která nám umožní dvojitou aplikaci předchozí habaďůry.

Na tom spodnim obrázku máme de facto dva "speciální" trojúhelníky. Jeden ohraničený červenou, modrou a šedou "přímkou" (označme ho T'), a druhý ohraničený červenou, zelenou a šedou (T+T'). Sice se nám tam nasáčkoval jeden úhel navíc (?), ale to nevadí. Plochu obou lehce vyčíslíme z té "speciální" formulky (+) a odečtením získáme hledanou plochu T.

P(T) = P(T+T') - P(T') = (?-ß-?-?) - (?-(?-?)-?) = ? - (?+ß+?)

A máme hyperbolický případ pod střechou:

plocha trojúhelníku se rovná úhlovému defektu (s opačným znaménkem).

Když si ten hyperbolický vzoreček porovnáte se sférickým případem, musíte ocenit jemnou harmonii, která v diferenciální geometrii vládne. Sférická a hyperbolická geometrie jsou určitými protipóly, zatímco ta eukleidovská je úzkým spojovacím můstkem mezi nimi.

V podstatě jsme zjistili, že neeukleidovské trojúhelníky jsou v jistém smyslu ještě vychovanější než ty eukleidovské. Pro ně lze totiž plochu spočítat z úhlového defektu - v kladném či záporném smyslu. Pro eukleidovské trojúhelníky to neplatí ani náhodou (to by musely mít všechny nulovou plochu). Ty si žijí ve svém vlastním světě.

+++++++++

Příklady

Abychom si ty vzorečky mohli trochu osahat, spočítáme si úhlový defekt sférického trojúhelníku Praha-Liberec-Hradec Králové. Samozřejmě za zjednodušujícího předpokladu, že Země je perfektní sféra s poloměrem 6371 km.

Nejprve si najdeme zeměpisné souřadnice (šířka a délka):

Praha (50.083333, 14.416667)
Liberec (50.766667, 15.066667)
Hradec (50.209167, 15.832222)

a z nich si spočítáme středové úhly v radiánech (a pro kontrolu i vzdušné vzdálenosti)

Praha-Liberec 0.0139454 (88.8459 km)
Praha-Hradec 0.0159838 (101.833 km)
Liberec-Hradec 0.0129206 (82.3172 km)

defekt pak dostaneme pomocí L'Huilierovy věty

tan2(?/4) = tan(1s) * tan(1(s-a)) * tan(1(s-b)) * tan(1(s-c))

kde a,b,c jsou strany trojúhelníku vyjádřené pomocí středových úhlů a s=(a+b+c)/2.

Po vyčíslení dostaneme na pravé straně

tan2(?/4) = 4.63465*E-10

a po odmocnění

tan(?/4) = .0000215282

arctan už s takhle malou hodnotou moc nehne, takže dostaneme

? = 0.0000861129 (v radiánech)
? = 0.00493391 (ve stupních)

Úhlový defekt je tedy prakticky zanedbatelný (protože vzhledem k Zeměkouli je vyšetřovaný trojúhelník docela maličký a chová se téměř eukleidovsky), ale pro větší trojúhelníky už by se s ním reálně muselo počítat.

+++++++++

Plošníci žijící na perfektně hladké sféře (vyrobené ze slitiny platiny a iridia) by ale zjistili další odchylky od eukleidovské geometrie.

Ze školy si například pamatujeme, že poměr obvodu kružnice k průměru je ? = 3.141592...

Plošníci by ale zjistili, že tento poměr je nejen jiný, ale že se dokonce mění s průměrem.

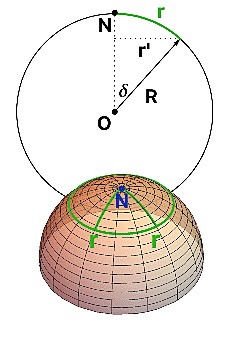
Podívejme se nejprve, jak si plošníci poradí s kružnicí (obr. vpravo). Na sféře s poloměrem R si zvolí nějaký bod, řekněme severní pól N, a pak od něho po nějaké přímce (geodetice) popolezou o vzdálenost r a tam si udělají do slitiny platiny a iridia zářez ve tvaru x. A ze všech těch zářezů nakonec vznikne ta zelená kružnice - tedy množina bodů, které mají od bodu N konstantní vzdálenost r.

Podívejme se jaký poměr plošníci naměří.

Jejich poloměr r je de facto kruhový oblouk odpovídající středovému úhlu ?. Vzhledem k němu můžeme poloměr jejich kružnice r vyjádřit pomocí poloměru sféry R: r = R ?.

Ta zelená kružnice je ale kružnicí i pro nás. Z našeho pohledu má ovšem jiný poloměr. Získáme ji tak, že sféru protneme rovinou p, ve které tato kružnice leží. V této rovině bude mít zelená kružnice běžný eukleidovský poloměr r' (viz obrázek vpravo), který se dá také vyjádřit pomocí středového úhlu: r' = R sin(?)

Obvod zelené kružnice je stejný pro nás i pro plošníky, a v rovině p ho dostaneme z běžné geometrie: o = 2? r' = 2? R sin(?)

Poměr obvodu kružnice a průměru bude tedy pro plošníky

o/2r = 2? R sin(?) / (2 R ?) = ? sin(?) / ?

Výraz sin(?) / ? je menší než 1, takže plošníci naměří o něco méně než ?. Současně se ale tento výraz limitně blíží 1 pro malé hodnoty ? a to znamená, že lokálně - pro malé zelené kružnice kolem pólu - naměří plošníci opět prakticky eukleidovské hodnoty.

+++++++++

A ještě jednu maličkost, která není na první pohled patrná.

Jedním z nejsilnějších nástrojů eukleidovské geometrie jsou podobné trojúhelníky, které mají stejné úhly, ale jejich strany jsou zmenšeny či zvětšeny v určitém poměru. Celá řada geometrických problémů se o tento pojem opírá, stejně jako středoškolská definice goniometrických funkcí.

Zajímavé je, že tato pozoruhodná geometrická květina vykvetla pouze v eukleidovské zahrádce. Ve sférické ani v hyperbolické geometrii nic takového neexistuje a kdybyste se na ni poptali v plošnické škole, odpovědí vám budou zmatené pohledy nechápavých 2D kukadel.

Ve sférické a hyperbolické geometrii se ze součtu úhlů dá odvodit plocha trojúhelníku a tím pádem také velikost jeho stran (poměřované příslušnou metrikou). To znamená, že v těchto geometriích existují pouze shodné (kongruentní) trojúhelníky, ale podobnosti tam pšenka nekvete.

Pokud v eukleidovské geometrii zvětšíte všechny strany v poměru řekněme a:1, pak se plocha trojúhelníku zvětší v poměru a2:1. A ničemu to nevadí: mezi plochou a součtem úhlů není žádná souvislost. Trojúhelník s danými úhly můžete libovolně zvětšovat a nebo zmenšovat. V neeukleidovských geometriích s ním můžete maximálně tak šibovat po ploše, ale jakmile ho trochu zvětšíte, okamžitě se zvětší i součet úhlů a už to nebude podobný útvar.

Podobnost je výsadou eukleidovské geometrie.

+++++++++

A rychle do říše hudby. Abychom se s westerny pořád neplácali v 50. a 60. létech, vybral jsem pro dnešek jeden modernější - Silverado z roku 1985. A našel jsem verzi, kde hudbu z tohoto filmu diriguje přímo pan skladatel. Tak si ji vychutnejte. Bruce Broughton: the Silverado theme

Předchozí díly Matykání.