Matykání: Pythagorovo souvětí

Pythagorova věta patří k základním kamenům středoškolských osnov. Dnes ovšem zjistíme, že má v každé geometrii svou specifickou podobu, takže to vlastně není věta, ale souvětí. Asi souřadné, neb souřadnicemi se to v něm jen hemží.

I plošníci žijící na zakřivených plochách si mohou nasliněnou inkoustovou tužkou nakreslit pravoúhlý trojúhelník z geodetik a zkoumat, zda mezi délkami jeho stran neexistují nějaké zajímavé vztahy.

A při pečlivém výpočtu se skutečně ukáže, že pythagorovské formulky pro sférický a hyperbolický pravoúhlý trojúhelník nejenže existují, ale vypadají jako by si z oka vypadly.

Na sféře geometři vykoumali, že přepona c a odvěsny a, b musí splňovat rovnici

cos(c) = cos(a) * cos(b)

zatímco na hyperboloidu se ty tři veličiny pojí takto:

cosh(c) = cosh(a) * cosh(b)

Z toho je mimochodem vidět, že mezi goniometrickými a hyperbolickými funkcemi existuje poměrně hluboký vztah, který jsme viděli již v komplexní analýze.

Navíc za okamžik uvidíme, že lokálně se obě Pythagorovy věty chovají eukleidovsky - tedy pro malé pravoúhlé trojúhelníčky se zmíněné rovnosti promění v tu, kterou známe ze školy:

c2 = a2 + b2

(stačí na jednu z výše uvedených rovnic ukázat kouzelným kružítkem a pronést zaříkávací formuli: dexempo multo federex)

Tyto tři podoby Pythagorovy věty jsou pro mne další ukázkou pozoruhodné harmonie, která v matematice vládne.

+++++++++

Sférický Pythagoras

Zatímco v eukleidovské trigonometrii nalezneme úhly uvnitř goniometrických funkcí a strany vně, ve sférické verzi se stranám podařilo do sínů a kosínů vlámat taky. Důvod je celkem jednoduchý.

Ve sférické geometrii de facto měříme vzdálenosti pomocí středových úhlů.

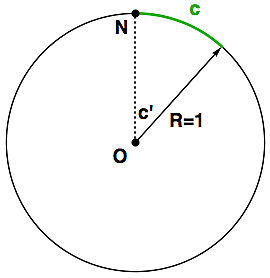
Na obrázku vpravo vidíme řez jednotkovou sférou a je celkem patrné, že naznačená délka zeleného sférického oblouku c je přímo úměrná středovému úhlu c'. Pokud ho měříme v radiánech, pak je dokonce c=c'. Pokud naše sféra jednotková není, stále existuje jednoduchá úměra mezi c a c':

c = R*c'.

Proto není problém uvažovat pro trojúhelník se stranou délky c výraz cos(c), protože ta délka se dá chápat (a taky chápe) jako úhel.

+++++++++

Nuže do díla.

Protože Pythagorova věta je v podstatě speciálním případem kosínové věty, odvodíme si nejprve její sférickou verzi.

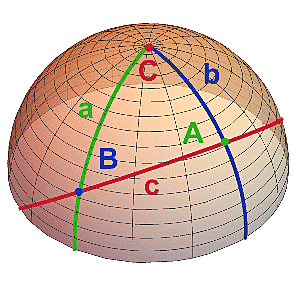
Vezmeme si trojúhelník ABC se stranami a, b, c a úhly A, B, C v odpovídajících vrcholech na jednotkové sféře se středem v bodě O.

Protože sféra je perfektně symetrická, můžeme si vhodnou rotací (aniž bychom změnili velikost stran či úhlů) natočit trojúhelník tak, aby vrchol C ležel na severním pólu a vrchol B na nultém poledníku (y=0). Bod A ať si pak padne, kam chce (viz obrázek vpravo).

Tři body trojúhelníku odpovídají třem vektorům:

u = OC
v = OB
w = OA

Středový úhel AOB má velikost c (délky stran odpovídají středovým úhlům) a protože všechny vektory jsou jednotkové, jeho kosínus bude roven skalárnímu součinu

cos(c) = v.w

Jen teď musíme najít správné vyjádření pro oba vektory v tradičních sférických souřadnicích, ve kterých bude zeměpisná šířka měřena od pólu a zeměpisná délka od zeleného poledníku.

Vektor v bude odpovídat šířce a a délce 0, takže jeho souřadnice budou

v = (sin(a),0,cos(a))

Vektor w má šířku b, délku C (viz obrázek) a tudíž souřadnice:

w = (sin(b)*cos(C),sin(b)*sin(C),cos(b))

Za skalární součin v.w proto dosadíme příslušný součin komponent

cos(c) = cos(a)*cos(b) + sin(a)*sin(b)*cos(C)

a to je v podstatě sférická verze kosínové věty.

Nyní položíme C = 90° a dostaneme Pythagorovu větu, která říká, že v pravoúhlém trojúhelníku na sféře splňují délky stran rovnici

cos(c) = cos(a)*cos(b)

+++++++++

Minule jsme při zkoumání úhlového defektu zjistili, že pro malé rozměry se sférické i hyperbolické trojúhelníky chovají podobně jako eukleidovské. Pojďme se tedy podívat, co se stane, když náš trojúhelník bude mít "maličké" strany a, b a c.

Pro malé hodnoty x se funkce cos(x) dá aproximovat kvadratickým polynomem

cos(x) ~ 1 - x2 / 2

(jsou to de facto první dva členy Taylorova rozvoje kosínu do "nekonečného polynomu")

Nuže dosaďme tuto aproximaci za jednotlivé členy sférické Pythagorovy věty:

(1 - c2 / 2) = (1 - a2 / 2) * (1 - b2 / 2)

Pravou stranu roznásobíme a po algebraické úpravě dostaneme

c2 = a2 + b2 - a2 b2 / 2

protože hodnoty a,b,c jsou malinké, člen a2 * b2 můžeme ve srovnání s ostatními zanedbat a dostaneme běžnou Pythagorovu větu.

c2 = a2 + b2

I zde tedy platí, že malé sférické trojúhelníky se chovají eukleidovsky.

+++++++++

Hyperbolický Pythagoras

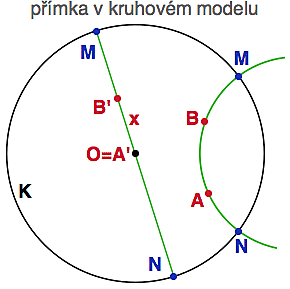
Protože minule jsme prováděli výpočet v modelu poloroviny, dnes se přesuneme do kruhového modelu a započítáme si tam. Naším pískovištěm bude jednotkový kruh K a "přímky" v něm budou představovat kružnice kolmé na K.

Přímka procházející body A a B je tedy (jednoznačně určená) zelená kružnice, jejíž konstrukci jsme zkoumali předminule. Tato kružnice protíná definiční kružnici K v bodech M a N.

Hyperbolickou vzdálenost mezi A a B budu značit d(A,B), zatímco pro běžnou eukleidovskou budu používat symbol AB. Neustále přepínání mezi eukleidovskými a hyperbolickými vzdálenostmi je asi nejtěžším aspektem hyperbolické trigonometrie.

Protože přímka (geodetika) je nejkratší spojnicí bodů A a B, vzdálenost d(A,B) mezi nimi se v principu spočítá tak, že si ten kousek zelené hyperbolické přímky (ať už vypadá jako kružnice nebo jako přímka) mezi A a B rozsekáme na spoustu malých infinitesimálních kousíčků, jeden každý z nich změříme příslušnou hyperbolickou metrikou a vzniklé mezivýsledky pak prostě sečteme (přesněji zintegrujeme, protože jsou infinitesimálně malé).

To je samozřejmě netriviální úkon a proto ho za nás pro obecnou (ne nutně jednotkovou) kružnici provedli báječní muži s logaritmickými pravítky a zjistili, že vzdálenost d(A,B) se dá vyjádřit pomocí tzv. křížového poměru běžných eukleidovských vzdáleností:

d(A,B) = | log(AM*BN / AN*BM) |

(to co je v závorce definuje křížový poměr uvedených bodů [A,B;M,N])

Pokud se stane, že jeden z těch dvou bodů je střed O jednotkové kružnice K, pak se ta zelená kružnice stane běžnou přímkou (kružnice s nekonečným poloměrem) a celý vzoreček se zjednoduší (viz obrázek nahoře). OM i ON budou rovny 1 (v našem případě je K jednotková kružnice) a pokud si označíme eukleidovskou vzdálenost mezi O a B' písmenkem x a dostaneme B'M = 1-x, B'N = 1+x, takže suma sumárum

(0) d(O,B') = | log((1+x)/(1-x)) |

(toto je de facto převod mezi eukleidovskou a hyperbolickou vzdáleností od středu)

Tento speciální případ OB' se dokonce dá odvodit přímo z metriky, protože na přímce je ta integrace poměrně snesitelná (podrobnosti zde a zde). A protože obecný případ d(A,B) se dá do počátku "dotlačit" pomocí Möbiových transformací, které zachovávají hyperbolické vzdálenosti, můžeme se při analýze trojúhelníku ABC omezit na situaci, kdy je bod A v počátku.

Nejprve ale rovnici (0) trochu přepíšeme. Pokud si tu hyperbolickou vzdálenost mezi O a B' označíme zkráceně jako d, můžeme ji vyjádřit pomocí exponenciely

(1) exp(d) = (1+x)/(1-x)

pro reciproké hodnoty pak dostaneme:

(2) exp(-d) = (1-x)/(1+x)

a pomocí hyperbolických funkcí můžeme (1) a (2) kombinovat:

(+) sinh(d) = 2x / (1-x2)
(++) cosh(d) = (1+x2) / (1-x2)
(+++) tanh(d) = 2x / (1+x2)

+++++++++

No a teď zpátky k té Pythagorově větě.

Nejprve si odvodíme dvě pomocné rovnosti.

(3) cos(A) = tanh(b) / tanh(c)
(4) sin(A) = sinh(a) / sinh(c)

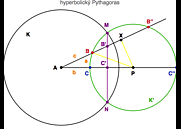
V trojúhelníku ABC necháme bod A v počátku O, takže dvě strany tohoto trojúhelníku budou (běžné) přímky, s tím, že pravý úhel bude ve vrcholu C. Třetí strana trojúhelníku bude odpovídat zelené kružnici K', kolmé na K.

Označme si na chvíli eukleidovskou vzdálenost AC písmenkem x. Protože C a C'' jsou inverzní vzhledem ke K (obě kružnice jsou vzájemně ortogonální a proto je K' inverzním obrazem sama sebe), platí:

AC'' = 1/AC = 1/x

a AP bude aritmetickým průměrem AC a AC'':

AP = (x+1/x)/2 = (1+x2) / 2x

Trojúhelníky AMP a AMC' jsou podobné, takže

AC'/AM = AM/AP

a protože AM = 1 (K je jednotková) dostaneme AC' * AP = 1, což znamená, že P a C' jsou inverzní body a platí tedy

AC' = 1/AP = 2x / (1+x2) =  tanh(b)

kde b je hyperbolická vzdálenost d(A,C), viz formulka (+++).

Eukleidovská vzdálenost AC' tedy představuje tanh hyperbolické vzdálenost b=d(A,C).

Podobně se ukáže, že AB' představuje tanh hyperbolické vzdálenost c=d(A,B).

Podíváme-li se na trojúhelník AB'C' eukleidovsky, máme

cos(A) = AC' / AB' = tanh(b) / tanh(c)

a to je přesně formulka (3).

+++++++++

A teď dokážeme formulku (4). A když už jsem si pracně nakreslil ten obrázek, ukážeme si ji nejprve pro sin(B) a pak prostě prohodíme proměnné.

Písmenkem x si pro změnu označíme eukleidovskou vzdálenost x=AB. Protože B a B'' jsou inverzní body vzhledem ke K (kolmost kružnic K a K'):

BB'' = AB'' - AB = 1/x - x = (1-x2) / x

což se dá podle formulky (+) převést na hyperbolickou vzdálenost c=d(A,B)

BB'' = 2 / sinh(c)

Obdobně jsou C a C'' inverzní body, takže analogicky dostaneme

CC'' = 2 / sinh(b)

Úhel B je roven úhlu (XPB).

To není úplně triviální, ale pokud si v bodě B sestrojíte tečnu k zelené kružnici a uvážíte, že tato je kolmá na BP, bude to jasnější. Pokud ne, kopněte do sebe štamprli a uvidíte to hned. Proto můžeme hodnotu sin(B) spočítat z trojúhelníku XPB (BP je to samé co CP a to je polovina CC''):

sin(B) = BX / BP = (BB''/2) / (CC''/2) = sinh(b) / sinh(c)

a pouhým přeznačením stran dostaneme rovnici (4)

sin(A) = sinh(a) / sinh(c)

(odpovídající přesunu vrcholu B do počátku a provedením téže úvahy)

+++++++++

Z formulek (3) a (4) už hyperbolickou Pythagorovu větu obdržíme celkem snadno.

Začneme s triviální rovností:

1 = sin2(A) + cos2(A)

na kterou obě formulky aplikujeme.

1 = sinh2(a) / sinh2(c)  +  tanh2(b) / tanh2(c)

Obě strany vynásobíme sinh2(c):

sinh2(c) = sinh2(a) + cosh2(c)*tanh2(b)

dále k oběma stranám přičteme 1 a uvážíme, že 1+sinh2(x)=cosh2(x):

cosh2(c) = cosh2(a)+cosh2(c)*sinh2(b)/cosh2(b)

a pronásobíme cosh2(b)

cosh2(c)*(cosh2(b)-sinh2(b)) = cosh2(a)*cosh2(b)

Závorka vlevo je rovna 1, takže už stačí jen odmocnit:

cosh(c) = cosh(a)*cosh(b)

A to je hyperbolická Pythagorova věta.

No, trochu jsem to ošulil, ale pokud se chcete v technických detailech pošťourat podrobněji, mrkněte sem anebo sem. A protože pro malá x platí, že cosh(x) ~ 1 + x2 / 2, stejně jako ve sférické geometrii se přesvědčíme, že limitně se hyperbolická Pythagorova věta blíží té eukleidovské.

+++++++++

Shrnutí neeukleidovských geometrií

Tak končí naše geometrie. Kosínus prohrává a Eukleides žije.

Čtenář by si teď mohl plným právem položit otázku, k čemu jsou ty neeukleidovské geometrie vlastně dobré.

U sférické je to jasné. Žijeme na sféře a její geometrie je geometrií našeho pohybu po ní. Kartografové o tom vědí své.

U hyperbolické je to otázka o něco ošidnější. V matematice se samozřejmě hyperbolická geometrie používá pro speciální účely (kromě diferenciální geometrie například v teorii čísel či dynamických systémů). Obecná teorie relativity je v podstatě studiem zakřivených prostorů. Ale existují i trochu esoteričtější aplikace, se kterými se lze setkat při studiu komplexních sítí, atomických struktur, celulárních automatů či zobrazování grafů.

A ruku na srdce - hyperbolická geometrie má i určitý dosah estetický.

+++++++++

V každém případě je jejich studium jednou z nejpodnětnějších oblastí matematiky, protože naše zkostnatělé eukleidovské vidění neustále natahuje na skřipec imaginace. Nutí náš mozek pohlížet na svět rybíma očima.

Ale protože těch odlišností jednotlivých geometrií bylo v průběhu této minisérie poměrně dost, podívejme se na závěr na jejich stručný přehled.

geometrie	hyperbolická	eukleidovská	sférická
realizace	pseudosféra	rovina	sféra
křivost	K<0	K=0	K>0
	?	1	0
	rozbíhavé	paralelní	sbíhavé
metrika	ds2/(1-x2-y2)	ds2	ds2/(1+x2+y2)

Několik upřesnění:

- počet rovnoběžek je vztažen k dané přímce a bodu, který na ní neleží

- chování rovnoběžek je přesněji chování přímek se společnou kolmicí: v eukleidovské si udržují stejnou vzdálenost, ve sférické se vzdálenost mezi nimi zmenšuje a v hyperbolické naopak zvětšuje

- poměr obvod:průměr se rozumí u kružnice

- součet vnitřních úhlů zase v trojúhelníku

- Pythagoras, pokud ho neznáte, je mimo jiné číselný mystik :-)

- metrika je vztažena k běžné eukleidovské, tj. ds2 = dx2 + dy2, a její přesný tvar závisí na konkrétním modelu

No a za staré Řecko je to ke geometrii asi tak fšecko.

+++++++++

Dnes se s neeukleidovskými geometriemi loučíme a protože loučení je vždycky tak trochu hořkosladká záležitost, vybral jsem na závěr soundtrack z poměrně neznámého westernu "The Desperados", jehož centrální téma (0:48) patří k nejkrásnějším hořkosladkým melodiím, které znám. David Whitaker: The Desperados.

Předchozí díly Matykání.