Matykání: pohádka o třech geometriích
Bylo nebylo, za devatero horami rozkládalo se malé království...
Stop! Počkat. Takhle matematickou pohádku začít nemůžeme. Jednak by si někdo mohl myslet, že zmíněné království zahnívá, ale hlavně by takový vágní úvod nerozdýchala lidová komise za formální preciznost matematiky. Takže druhé podání. Second service.
Nechť K je kompaktní jednoduše souvislé království a devítirozměrný hřebenový vektor H=(h1, h2,... h9) nechť označuje horské útvary, za kterými se království nalézá. Tak teď už to snad projde. No a v tomto království kdysi dávno moudře vládla královna Lichoběžnice (sorry, milé děti, krále Lichoběžníka mi zamítla lidová komise pro otázky genderové vyváženosti). Jedné bouřlivé srpnové noci se za dosud nevyjasněných okolností oblíbené vladařce z rodu čtyřúhelníků narodila princezna Rovnoběžka. Původně jsem chtěl dát k dobru několik veselých příhod z období jejího dospívání (například jaké lumpárny prováděla s kružítkem nebo jak v zámecké zahradě potajmu dělila nulou), ale proškrtala mi je lidová komise na ochranu osobních dat, takže se spokojíme s konstatováním, že 9. srpna se princezna Rovnoběžka za dosud nevyjasněných okolností dožila ?3/sqrt(e) let. V prvním náčrtu pohádky jsem napsal na tvrdo "devatenácti let", jenže lidová komise pro práva utlačovaných množin mi velmi přátelsky sdělila, že iracionální čísla jsou v pohádkách hrubě diskriminována a proto jsme se za dosud nevyjasněných okolností dohodli na výše uvedeném kompromisu.
Ale dost legálního kličkování. Pojďme k meritu věci.
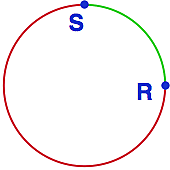
V den svých narozenin se princezna rozzlobila, že se nemůže protínat s ostatními přímkami (a hlavně přímáky) - jako její zkušenější vrstevnice - a tak si sbalila svých pět švestek, za klobouček si strčila úhloměr a jednoduše práskla do koní. Celou noc rovnoběžela zarostlou pěšinkou podél dálnice D, až doběhla k pozorovacímu stanovišti S, kde zmizela v hustém lesíku L (což, pokud to nevíte, je spočetné sjednocení několika lokálně hustých porostů Baireovy třetí kategorie).
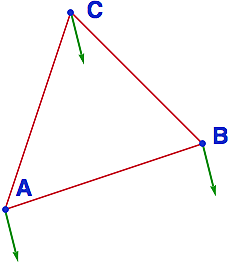
Když se královna probudila, nechala osedlat exponenciální funkci a vyrazila za princeznou. Když zahlédla stanoviště S, scválala z dálnice D a za několik vteřin se ocitla u plátěné boudy, za níž vartovali tři veteráni. "Osoby!", zhurta se na ně obořila, "neviděli jste tudy probíhat princeznu Rovnoběžku?"
Jako první se zorientoval svobodník Bystrozraký, který měl podle svého zvyku oči převázané šátkem: "Já nic nevidím, takže podle mne tu vůbec žádná Rovnoběžka neběžela."
Jako druhý se ozval desátník Dlouhý, který měl z pozice své výšky o všem výborný přehled a neochotně zamrmlal: "Ale jó, jednu takovou cácorku jsem tady viděl. Mazala odsud pryč tak rychle, až jsem měl strach, že se jí zavaří čtverce nad oběma odvěsnami".
Nakonec se probral i četař Široký a svíraje v rukou nedopitou láhev pálenky z nakvašených logaritmů, několikrát zamžoural, jako by se pokoušel zaostřit na věžní hodiny v nekonečnu. "Paní královno, škyt, nebudete mi to věřit, škyt, ale já těch utíkajících princezen viděl hned několik."
Nu, princeznu sice nechytili, ale veteráni se - jak bylo v království zvykem - poměrně úspěšně uplatnili jako suplující pedagogové ve školství. Jen každý z nich svým žákům vykládal trochu jinou geometrii.
Svobodník Bystrozraký tvrdil, že bodem S neležícím na přímce D neprobíhá žádná rovnoběžka. Desátník Dlouhý tvrdil, že takovým bodem probíhá právě jedna rovnoběžka a četař Široký tvrdil, že rovnoběžek procházejících bodem S existuje hned několik.
Kdyby to viděla lidová komise pro koordinaci jednotné výuky, tak je snad zavřou.
+++++++++
Když ve škole zápolíme s Pythagorovou větou, s konstrukcí kružnice vepsané či s obsahem lichoběžníku, ani nás nenapadne, že by mohla existovat nějaká jiná geometrie než ta, kterou jsme se za dvanáct let povinné docházky pracně našprtali. Ale opak je pravdou.
Geometrie je - stejně jako většina matematiky - vybudována axiomaticky.
To znamená že v ní existují dva typy tvrzení.
1. Axiomy (čili Postuláty), které jsou natolik očividné, že jejich pravdivost předpokládáme. Jinudy vlak prostě nejede a basta fidli.
2. Věty (čili Teorémy), které se z těch axiomů dají odvodit pomocí logických pravidel.
Každá dobrá teorie se snaží, aby měla axiomů co nejméně.
V srdci geometrie leží pět Eukleidových postulátů (pokud jste je zapoměli - tady jsou), z nichž první čtyři jsou poměrně jednoduché, ba dalo by se říci triviální, zatímco ten pátý je poměrně komplikovaný. V moderní podobě ho známe jako Playfairův axiom:
Bodem B neležícím na přímce p lze vést právě jednu rovnoběžku.
Po několik století matematikům připadalo, že tato formulace je zbytečně složitá a že se tedy axiom dá pravděpodobně nějak dokázat z prvních čtyř. A nespočet generací geometrů se snažilo platnost pátého postulátu odvodit z těch předchozích. Marně.
Teprve na začátku 19. století se několik chrabrých matematiků (mj. Carl Friedrich Gauss, Nikolaj Lobačevski a Janos Bolyai) rozhodlo jít opačnou cestou a začali hledat fungující geometrii, která by splňovala všechny axiomy, s výjimkou toho pátého. A protože vědecká komunikace v té době byla žalostně pomalá (nalézáme se 150 let před Internetem), své úvahy a konstrukce rozvíjeli nezávisle na sobě. Výsledkem jejich snažení byly základy geometrie, které dnes říkáme "hyperbolická" (zajímavý link najdete zde).
Skutečným průlomem do našeho chápání geometrie byla habilitační práce Bernharda Riemanna z roku 1854, ve které autor ukázal, že geometrické vlastnosti daného prostoru se odvíjí od jeho zakřivení. Riemannova práce se týkala především prostorů s kladnou křivostí (zobecnění sfér), ale jeho výsledky brzy zobecnili do prostorů se zápornou křivostí Eugenio Beltrami a Henri Poincare. A v podstatě od těch dob je studium různých typů geometrií studiem geometrických vlastností zakřivených ploch či prostorů.
A to bude nosným tématem dnešního Matykání.
+++++++++
Co je geometrie?
Ve škole má geometrie svoje nezastupitelné místo. Seznámíme se s body a přímkami. Zvládneme Pythagorovu větu. Naučíme se využívat podobnost trojúhelníků ku prospěchu svému. Ba někdy i ku prospěchu svého vysvědčení.
Všechno je to ale eukleidovská geometrie v rovině.
Představme si pro změnu nějakou dvourozměrnou zakřivenou plochu (či techničtěji varietu), ve které žijí dvourozměrní "plošníci". Jejich plochosvět má pouze dva rozměry: dopředu-dozadu a doleva-doprava. Nějaké nahoru-dolů se vyskytuje pouze v jejich sci-fi románech a to ještě pouze v případě, že se pan autor pořádně zlíská.
I plošníci pochopitelně chodí do školy, kde se naučí spoustu užitečných věcí - např. jak vkládat 2D bábovku do trouby, či jak chytit 2D krávu do lasa. Pojďme se tedy zamyslet, co se asi učí v hodinách geometrie.
Především se musí nějak popasovat s body. To není problém. I zakřivená plocha (jejich svět) se skládá z jednotlivých bodů, takže můžeme začít spekulovat, co by se z těch bodů dalo poskládat. Přímky, tak jak je chápeme my, v jejich světě ovšem neexistují, protože běžná přímka (procházející nějakým bodem P) by z té plochy žalostně trčela ven a tam ji plošníci neuvidí (oni z té 2D plochy nedokáží "vyhlédnout" ven, stejně jako my nedokážeme "vyhlédnout" z našeho 3D prostoru).
Přesto o tuto část geometrie ochuzeni nebudou.
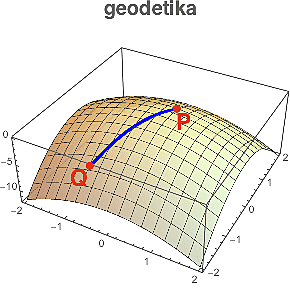
V tom jejich zakřiveném plochosvětě stále existují souřadnice (zvlněné křivky na obrázku, ze kterých je ta plocha "utkaná"), takže plošníci budou schopni měřit vzdálenosti. Úsečku procházející danými body P a Q si tedy mohou definovat jako nejkratší možnou křivku tyto body spojující. Takových spojnic je obecně celá řada, ale oni si je pěkně všechny přeměří a tu nejkratší prohlásí za úsečku PQ (jejímž prodloužením oběma směry pak vznikne kýžená přímka).
Takto vzniklé "přímce" říkáme geodetika či geodetická křivka (angl. geodesic). Můžete si ji představovat třeba tak, že po zakřivené ploše táhnete sáňky, které v hlubokém sněhu obvykle dobře udržují směr, přestože je taháte po kopcích a dolinách. Při pochodu podél geodetiky se tedy z pohledu plošníků nebudeme vychylovat ani doprava, ani doleva, ale půjdeme stále "rovnou za nosem" (přestože z našeho lidského 3D pohledu se jedná o pochod "lehce zvlněný").
A jakmile máme rozumně definované "přímky", můžeme budovat geometrii. Vezmeme si tři body, spojíme je geodetikami a ejhle - dostaneme trojúhelník. A hnedle můžeme začít zkoumat, jaký je jeho obsah či zda v něm platí věta kosínová.
+++++++++
Abychom si tu křivočarou geometrii mohli trochu "osahat", pojďme se podívat na jednoduchý příklad, kdy naší plochou bude 2D sféra. Protože žijeme na povrchu jedné takové velkokoule, bude nám tato geometrie minimálně povědomá.
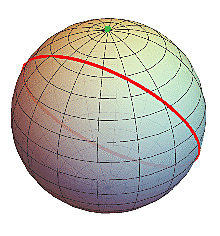
Nejkratší spojnice bodů P a Q na sféře (se středem v bodu O) je kružnice vzniklá jejím průsečíkem s rovinou POQ. Takovým křivkám říkáme velké (či hlavní) kružnice a ty představují geodetiky naší 2D plochy (sféry). Podél nich létají letadla, pokud zrovna není bouřka na trase. Všechny poledníky jsou geodetikami, rovnoběžky - s výjimkou rovníku - nikoliv (rovina, která je na sféře vysekne, neprochází středem). Pokud vám to není úplně zřejmé, představte si severní polární kruh. Kdyby byl geodetikou (tj.sférickou přímkou), pak by byl nejkratší spojicí dvou protilehlých bodů na něm ležících (což není - kratší trasa bude, když si to střihnete přes pól).
V eukleidovské geometrii prochází každým bodem P nekonečně mnoho přímek (jedna pro každý směrový vektor u), což je nejlépe vidět na parametrické rovnici přímky:
x = P + tu (kde t je reálný parametr ukazující, kde se na přímce nalézáme)
Podobně si i na naší zakřivené ploše sféře můžeme v bodě P vybrat směr (tady bude vektor u technicky vzato pocházat z tečného prostoru v tomto bodě) a vyrazit podél něho na cestu. Protože je sféra symetrická, můžeme si představit, že bod P leží severním pólu a každá geodetika pak bude odpovídat pochodu podél jednoho poledníku (naše znalosti zeměpisných souřadnic nám tak umožní vybudovat si geometrickou intuici).
Poledníky představují soubor "přímek" (geodetik) procházející konkrétním bodem P a můžeme je s úspěchem využít k dalším úvahám. Pokud náš bod P není severní pól, tak sféru pootočíme, aby byl.
Ale musíme být opatrní: zatímco přímka je definovaná globálně (v celé rovině), geodetiky jsou typicky definovány pouze lokálně (v nějakém okolí bodu P), protože obecně vůbec netušíme, jakým způsobem se náš prostor křiví, pokud z bodu P trochu poodejdeme - může tam být horský hřeben či rokle atd. Lokálně se tedy geodetiky chovají jako přímky, ale globálně mohou mít i poměrně neočekávané vlastnosti. Tím pádem je analýza geodetik podstatně delikátnější než analýza přímek.
Například se může stát, že vyrazíme ze severního pólu S podél nějakého poledníku k jihu (schematicky na obrázku vpravo), profrčíme rovníkem, profrčíme jižním pólem a zastavíme se při dalším průchodu rovníkem v bodě R. Ta červená kružnice naší trasy bude stále geodetikou, ale už nebude nejkratší spojnicí bodů S a R (tou bude jiná geodetika - ta zelená). Takže taková ta heuristika, že geodetiky jsou nejkratší spojnice bodů platí pouze lokálně. Na sféře máme kliku, že ta zelená geodetika je pokračováním té červené - ale na obecné varietě to platit nemusí - zkuste si najít příklad třeba na toru.
(ta lokálnost je do geodetik obecně zabudována tím, že tyto jsou definovány řešením diferenciálních rovnic, která jsou svou povahou lokální - jakmile se z bodu P přesuneme kousek dál, musíme celou situaci přehodnotit, vyřešit další rovnici na okolí nového bodu a celou trasu pak z těchto lokálních "záplat" pospojovat - sféra je ale dostatečně "ukázněná" plocha, kde se geodetiky dají definovat globálně, takže v tomto případě si s tím nemusíme lámat hlavu)
+++++++++
Jakmile se se sférickými geodetikami jakž takž skamarádíme, hned nám začnou vyskakovat problémy.
Především (viz obrázek vpravo), když si za body P a Q zvolíme severní a jižní pól (zeleně), vidíme, že existuje nekonečně mnoho geodetik (nejkratších tras), tyto body spojující (jeden každý poledník). V eukleidovské rovině je přímka procházející dvěma různými body určena jednoznačně.
Nebo trochu komplikovaněji: představte si, že stojíte na východním úpatí Řípu v bodě P a váš kamarád stojí na druhé straně (západní úpatí) v bodě Q. Pokud bude Říp dostatečně vysoký (aby nejkratší spojnice PQ nevedla přes vrchol), budou existovat dvě geodetiky (zde by se dalo říci "polabské přímky") spojující body P a Q. Jedna podél severního úpatí, druhá podél jižního. V tomto případě je tedy geodetika PQ určena dvojznačně (a to je jeden z důvodů, proč je lepší na ně nahlížet lokálně, kde s jednoznačností nejsou problémy).
I rovnoběžky - myslím teď matematické, ne zeměpisné - se chovají "divně". Definujme si je pro jednoduchost jako dvě přímky, které nemají žádný společný bod. V eukleidovské geometrii platí, že bodem P neležícím na přímce p prochází právě jedna rovnoběžka s přímkou p (výše zmíněný axiom).
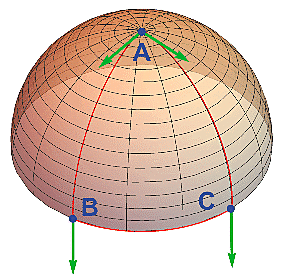
Vezměme si tedy za naši přímku p červenou hlavní kružnici z předchozího obrázku (což je geodetika - tedy sférická "přímka"). Za bod P si vybereme (aby se nám ty geodetiky procházející bodem P lépe představovaly) opět severní pól (zelený bod). A zkuste teď mezi všemi těmi poledníky z bodu P najít nějaký, který neprotíná tu červenou kružnici. Máte smůlu. Takový neexistuje. Ve sférické geometrii tedy bodem ležícím mimo přímku neprochází žádná rovnoběžka.
A což teprve, když začneme věci měřit.
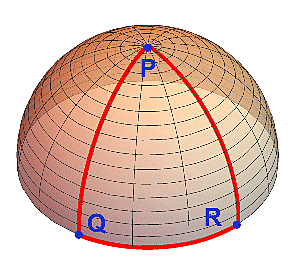
Ve škole se učíme, že součet vnitřních úhlů v trojúhelníku je 180°. Nahlédněme tedy do učebnice plošníků na sféře.
Vezmeme si jednoduchý trojúhelník spojující severní pól P se dvěma body na rovníku Q a R. Oba úhly v bodech Q a R jsou evidentně pravé a pokud si označíme úhel v bodě P symbolem ?, zjistíme že součet vnitřních úhlů v trojúhelníku PQR je 180°+? (může to tedy být prakticky cokoliv mezi 180° a 360° - podle toho kam na rovníku posadíme body Q a R).
Tohle by nám trojúhelník v eukleidovské rovině nikdy neudělal.
Nabízí se tedy 3 důležité otázky.
1. Dá se v té křivočaré geometrii vůbec něco dokázat?
2. Má každá plocha svou vlastní geometrii a nebo v nich existuje nějaký řád?
3. Dá se ten řád rozpoznat "zevnitř", bez nutnosti kouknout na plochu "zvenčí"?
Těmito otázkami se budeme zabývat v této sérii.
A zjistíme, že plošníci se skutečně mohou domáknout toho, na jaké ploše žijí pouhým zkoumáním geometrických vlastností svého světa. Tedy "zevnitř". Stejně jako my bychom se mohli dopídit toho, že žijeme na sféře pouze přesným proměřováním geometrických útvarů, aniž bychom naši planetu museli obeplouvat na lodi nebo na ni koukat z vesmíru (naše pozice by ovšem byla ztížena tím, že Země není perfektní sféra - je trochu zploštělá a jsou na ní hory a údolí a jiné odchylky od kulatosti).
A protože tak nějak intuitivně cítíme, že za to, že se nám rozsypala eukleidovská geometrie může zakřivení, podíváme se mu trochu na zoubek.
(nevrč brachu na Eukleida, když máš sféru křivou)
+++++++++
Křivost křivek
Jakýmsi etalonem pro poměřování zakřivení je v 1D případě kružnice. Její křivost je definována jako reciproká hodnota poloměru k = 1/r, což odpovídá naší intuitivní představě, že čím větší kružnice, tím menší křivost (a v limitním případě přímky - kdy se poloměr kružnice blíží nekonečnu - dostaneme podle očekávání k=0).
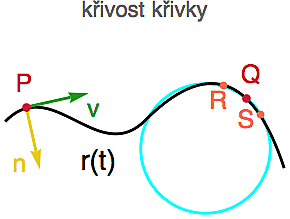
Křivost rovinné křivky se obecně mění a v nějakém zvoleném bodě Q ji můžeme dostat například tak, že v tom bodě křivku aproximujeme co "nejpřiléhavější" kružnicí, jejíž poloměr R nám umožní spočítat hledanou křivost k(Q) = 1/R.
Stejně jako má každá (dostatečně hladká) křivka v každém bodě tečnu (tedy "nejpřiléhavější" přímku), má i nejlepší lokální aproximaci kružnicí. Říkáme jí oskulační kružnice dané křivky v bodě Q (na obrázku vpravo v bledě modrém) a můžete si ji představit takto. V okolí bodu Q si na křivce vyberte další dva body R a S. Body Q, R a S prochází právě jedna kružnice K (v podstatě kružnice opsaná trojúhelníku QRS). A když teď budeme body R a S spojitě přibližovat k bodu Q, tak se z kružnice K v limitním případě stane právě oskulační kružnice.
Tento proces není výpočetně zrovna nejpřitažlivější (byť je dobrý pro intuitivní uchopení pojmu křivosti), proto se vzoreček pro křivost obvykle odvodí pomocí diferenciálního počtu z parametrizace křivky (to je důvod, proč se této partii matematiky říká diferenciální geometrie).
Rovinné křivky můžeme popsat pomocí dvou funkcí parametru t. Ten má většinou význam času, takže ta parametrizace nám de facto říká, jak se polohový vektor r(t) = (x,y) mění s časem t.
x = f(t)
y = g(t)
Asi nejznámější je parametrizace kružnice
x = sin(t)
y = cos(t)
Každý bod na křivce tedy odpovídá jedné hodnotě reálného parametru t a jak tou křivkou pomalu projíždí, v každém bodě má jednoznačně určený tečný vektor v (na předchozím obrázku zeleně), který si můžete představit jako vektor momentální rychlosti (ukazuje vám, kterým směrem se právě pohybujete).
Křivost je pak zhruba řečeno rychlost s jakou se tento tečný vektor v mění během pohybu po křivce. Tam, kde je křivka křivá se mění poměrně rychle, tam kde je vcelku rovná pak pomalu (na této animaci wikipedie je tečný vektor zelený, normálový žlutý a uvidíte tam i oskulační kružnici).
Tečný vektor v se spočítá podobně jako rychlost - tj. spočítáme rozdíl poloh pro malý časový interval dt a tímto následně vydělíme
v(t) = ( r(t+dt) - r(t) ) / dt
no a pak už jen sledujeme jak se ten podíl chová pro zmenšující se hodnoty t (technicky vzato zkoumáme jeho limitu pro t › 0), což je v podstatě definice derivace r podle t (tj. jak rychle se mění proměnná r v závislosti na proměnné t). A protože nás zajímá změna této rychlosti s časem (tedy de facto derivace derivace), objeví se nám ve vzorečku druhé derivace výše uvedených funkcí. Protože je ale současně nutné všechno přepočítat na jednotkovou délku křivky, není jeho odvození zrovna procházka růžovým sadem. Pro křivost v bodě odpovídající parametru t dostaneme:
k(t) = (x'y''-x''y')/sqrt(x'2+y'2)3
(derivace parametrizačních funkcí jsou obvykle naznačeny čárkami, popř. tečkami)
Pokud rádi derivujete, dosaďte si tam výše uvedenou parametrizaci kružnice a mělo by vám vyjít k(t)=1 pro každou hodnotu parametru t.
Sečteno a podtrženo: ten výpočet křivosti křivek je trochu zapařený, ale oskulační kružnice nám umožňuje o ní stále uvažovat poměrně srozumitelným způsobem.
+++++++++
Křivost ploch
Zakřivit se dokáží i 2D plochy (lidské tělo budiž důkazem).
Problém s definicí křivosti v tomto kontextu spočívá v tom, že 2D plocha se může současně křivit mnoha různými způsoby.
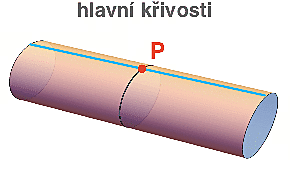
Vezměme si například válec znázorněný na obrázku vpravo. Pokud vyrazíme z bodu P podél modrého směru, pohybujeme se po obyčejné eukleidovské přímce s nulovou křivostí. Pokud vyrazíme podél směru černého, pohybujeme se de facto podél kružnice s křivostí 1/r.
A pokud vyrazíme v nějakém směru mezi tím (a dál pokračujeme podél příslušné geodetiky - tj. necháme sáňky jet kam chtějí), naše dráha na válci vysekne křivku, jejíž křivost v bodě P bude někde mezi 0 a 1/r.
Plocha má tedy v každém bodě nekonečně mnoho křivostí (jednu pro každý směr - resp. tečný vektor). A není úplně jasné, zda se z nich dá vůbec vykouzlit jedno číslo, které by tu křivost nějak rozumně charakterizovalo. Zkusíme to trochu formalizovat.
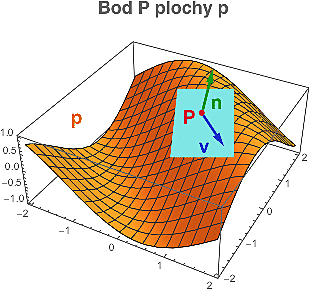
Nuže, vzhůru na šikmou (a ladně zakřivenou) plochu p!
V bodě P vztyčíme normálový vektor n, který je kolmý na bledě modrou tečnou rovinu (viz obrázek vpravo). Tím normálovým vektorem můžeme vést nekonečně mnoho rovin (určených vektorem n a jedním s tečných vektorů v). Každá taková rovina vysekne z oranžové plochy rovinnou křivku, jejíž křivost k(v) už umíme spočítat či změřit.
Takže v každém bodě P máme celou škálu "směrových" křivostí k(v), jednu pro každý směr určený tečným vektorem v. A co teď s nimi?
Jedním ze způsobů, jak z nich vyždímat jedno jediné číslo je vzít si průměr, což vede k pojmu střední křivosti. Gauss si ale při svém zkoumání ploch povšiml, že existuje způsob, který je jednodušší a navíc nás dovede k velmi zajímavému číslu.
Mezi všemi těmi směrovými křivostmi je jedna největší a jedna nejmenší. Pokud si příslušné směry označíme v a w, můžeme tyto křivosti zapsat jako k(v) a k(w). Říkáme jim hlavní křivosti a příslušným směrům - o kterých se dá ukázat, že jsou navzájem kolmé - pak hlavní směry (křivosti). Výše uvedený válec má tedy dva hlavní směry: černý v a modrý w, s tím, že příslušné křivosti jsou k(v)=1/r a k(w)=0.
To že ty hlavní směry jsou kolmé není úplně nabíledni. V bodě P si musíte zvolit souřadnice tak, aby tečná rovina odpovídala rovině x-y. Pak se dá plocha aproximovat kvadratickým polynomem q(x,y) = ax2 + 2bxy + cy2, který lze zapsat maticově pomocí tzv. kvadratické formy (Au,u), kde u=(x,y) a A je matice ((a,b),(b,c)). Hlavní směry jsou pak vlastní vektory této matice (symetrické matice mají kolmé vlastní vektory!) a hlavní křivosti jsou její vlastní čísla (viz též shape operator).
Součinu obou hlavních křivostí říkáme Gaussova křivost K = k(v).k(w). Tento zdánlivě primitivní konstrukt má při studiu zakřivených ploch zcela fundamentální význam, protože se nemění pokud plochu pouze rigidně ohýbáte (aniž byste ji roztahovali). Představuje tedy důležitý invariant, který - jak se později ukázalo - určuje typ geometrie zakřivené plochy a dovede nás k jejich klasifikaci.
Například válec z prvního příkladu má Gaussovu křivost K=0 (protože hlavní křivosti jsou 0 a 1/r), stejně jako běžná eukleidovská rovina. Válec má tedy (přes své zakřivení v jednom směru) stále eukleidovskou geometrii a většinu těch ošklivých věcí, které jsme výše nalezli na sféře (např. součet úhlů v trojúhelníku není 180°) na něm nenajdeme.
To není zase až tak absurdní, představíme-li si rovinu jako milimetrový papír. Jejím srolováním do válce se délky jednotlivých "čtverečků" nijak nedeformují. Válcoví plošníci by tedy žádné lokální odchylky od eukleidovské geometrie nenaměřili. Pouze pokud by plošníci ten válec kompletně obepluli, zjistili by, že jejich svět není rovinou, jak si původně mysleli (a jak jim jejich geometři tvrdili).
Sféru oproti tomu žádným "chytrým" rolováním papíru nevytvoříte. Proto nemá na eukleidovskou geometrii nárok. Její Gaussova křivost je kladná: K=1/R2 (obě hlavní křivosti jsou k=1/R) a sféričtí plošníci by proměřováním pravoúhlých trojúhelníků velmi rychle zjistili, že jejich Pythagorova věta je úplně jiná než ta naše (časem se na ni podíváme).
Gauss byl tímto objevem natolik nadšen, že ho pojmenoval "Pozoruhodná Věta" (Theorema Egregium). Ta se stala základem našeho poznání, že charakter geometrie dané plochy se dá zjistit "zevnitř" - tedy studiem úhlů a vzdáleností, aniž bychom museli tuto plochu opustit, abychom se "zvenčí" podívali, jak je přesně vnořená do okolního prostoru.
+++++++++
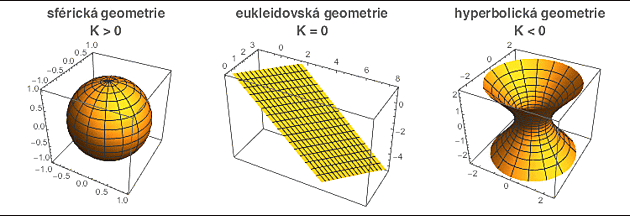
Tři typy geometrií
V souvislosti s Gaussovou křivostí musíme věnovat pozornost jednomu aspektu, který jsme doposud trochu opomíjeli - znaménku. To je věcí konvence a v podstatě závisí na tom, zda si normálový vektor (kolmý k tečné rovině) vybereme na jedné straně plochy a nebo na druhé.
Pokud stojíme na sféře, zdá se nám, že se v obou hlavních směrech křiví směrem "dolů" (a na sféře si ty směry můžeme zvolit libovolně). Stojíme-li uvnitř sféry (jako malý pajdulák uvnitř fotbalového míče), sféra se bude v obou směrech křivit směrem "nahoru". Ať si tu normálu vybereme tak či onak, Gaussova křivost nám vyjde kladně (buď jako plus-krát-plus a nebo jako mínus-krát-mínus).
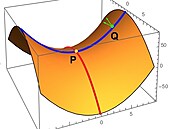
Existují ale typy ploch, které mají zápornou Gaussovu křivost - to znamená, že v jednom hlavním směru se plocha křiví směrem "nahoru", zatímco v tom druhém "dolů". Klasickým příkladem takové plochy je horské sedlo. Podívejme se na něj trochu podrobněji (obr. vpravo).
Představme si, že stojíme ve žlutém bodě P. Hlavní směry křivosti jsou vyznačeny modře a červeně. V jednom z nich se plocha křiví dolů, ve druhém dolů nahoru. Ať si vybereme normálu jakkoliv, jejich součin - tj. Gaussova křivost - bude záporný.
Ta červená křivka (odpovídající jednomu z těch hlavních směrů) je geodetika, což lze nahlédnout tak, že pokud si na ní vybereme nějaký další bod R, nenalezneme žádnou kratší cestu jak se k němu dostat. Z pohledu plošníků žijících na této ploše bude tedy reprezentovat přímku. A nyní se podél modré geodetiky (v druhém hlavním směru) vyškrábeme na úbočí do bodu Q a vyšleme kontrolního chrousta po další geodetice ve směru kolmém na modrou geodetiku (tedy zhruba "po vrstevnici"). Tato geodetika nikdy tu červenou geodetiku neprotne a bude tedy (podle naší zjednodušené definice) rovnoběžkou.
A nejen to: my můžeme chrousta vyslat směrem malinko "pootočeným" a ani jeho dráha se díky zakřivení sedla s tou červenou geodetikou neprotne. Jak moc ten kolmý směr můžeme pootočit závisí na poloze bodu Q a křivosti sedla (časem uvidíme model, ze kterého to bude patrnější). Důležité je, že všechny geodetiky, vyslané z bodu Q směrem mezi oběma zelenými vektory se nikdy neprotnou s tou červenou. A to znamená, že na ploše s negativní Gaussovou křivostí existuje k červené "přímce" ne jedna rovnoběžka procházející bodem Q, ale hned nekonečně mnoho.
+++++++++
Takže si to shrňme.
Gaussova křivost K je reálné číslo a jako takové může být buď kladné, nulové a nebo záporné. A tomuto rozdělení přesně odpovídají tři typy možných geometrií: sférická (geometrie povrchu koule), eukleidovská (geometrie roviny) a hyperbolická (geometrie horského sedla). Proč se jí říká hyperbolická uvidíme příště.
Ve sférické geometrii neprochází bodem ležícím mimo danou přímku žádná rovnoběžka (tuto geometrii učí ve své škole svobodník Bystrozraký), v eukleidovské geometrii prochází bodem mimo přímku právě jedna rovnoběžka (tak to učí desátník Dlouhý) a v hyperbolické geometrii takových rovnoběžek existuje nekonečně mnoho (jak se dušuje četař Široký).
Charakteristických rysů podle kterých daný typ geometrie rozpoznáme je pochopitelně mnohem víc. Např. ve sférické geometrii mají trojúhelníky součet vnitřních úhlů vždy více než 180°, v eukleidovské přesně 180° a v hyperbolické méně než 180° (to ale uvidíme až časem).
Nejlépe se tyto geometrie realizují na plochách, které mají konstantní Gaussovu křivost (hodnota K se nemění bod od bodu). Pro sferickou geometrii je to sféra, pro eukleidovskou běžná rovina a pro hyperbolickou zvláštní plocha, které se říká pseudosféra.
Existují ale poměrně jednoduché 2D plochy, které mají mixovanou křivost - charakter geometrie se pak mění podle toho, kde zrovna stojíte - například torus, na kterém najdete oblasti s nulovou, kladnou i zápornou křivostí (ne nutně konstantní).
To platí dvojnásob o obecných zakřivených plochách (jako ta z dnešního úvodního obrázku), kde najdete oblasti se sférickou, hyperbolickou i eukleidovskou geometrií (podle konkretní křivosti v tom či onom místě).
Tento fenomén ostatně nalezneme i na naší Zeměkouli. Ona má sice globálně tvar koule, takže odhlédneme-li od drobných odchylek, geometrie na ní je v zásadě sférická. Lokálně (při podrobnějším zkoumání odchylek od tvaru perfektní koule) na ní ale najdeme všechny typy geometrií.
Na vrcholku Řípu (přestože to není perfektní polosféra) bude panovat geometrie sférická, tj. geodetické trojúhelníčky, které si tam vytyčíte budou mít součet úhlů nad 180°. V Krkonoších na horském sedle bude panovat geometrie hyperbolická a tamější trojúhelníčky budou mít součet úhlů pod 180°. A konečně pokud si v Polabí postavíte tenisový kurt a pomocí vodováhy ho vyválcujete do precizní roviny, trojúhelníčky v něm vám na úhlech dají přesně 180°.
+++++++++
Sekce Jauvajs: paralelní transport I.
jen pro poněkud otrlejší povahy
Zakřivení prostoru lze detekovat i pomocí nepřímých ukazatelů. Jeden z rozdílů mezi plochými a zakřivenými prostory spočívá v chování tečných vektorů při jejich přenášení podél křivek.
V běžném Eukleidově prostoru nepředstavuje přenos vektoru z jednoho bodu do druhého žádný problém (viz obrázek). Prostě čapneme vektor za flígr a dotáhneme ho z bodu A do bodu B tak, aby si stále udržoval tentýž směr. To je možné proto, že naše plocha je v tomto případě zcela plochá a její tečný prostor je tudíž v každém bodě stejný (Eukleidovský prostor je v podstatě v každém bodě sám sobě tečným prostorem). Tím pádem jakýkoliv směr v bodě A se dá lehce replikovat v bodě B.
Podél červené trajektorie si ten vázaný zelený vektor můžeme představit tak, že uděláme jeden krok doprava a čtyři kroky dolů. Díky přirozené identifikaci tečných prostorů (ve kterých tečné vektory žijí) podél naší trajektorie nemáme žádný problém přenést vektor v z bodu A do bodu B a pak přes bod C zpátky do bodu A (technicky tomu říkáme rovnoběžný či paralelní přenos). Stačí dbát na to, aby se souřadnice během přenosu neměnily.
Specielně bych ale zdůraznil skutečnost, že v okamžiku, kdy se vrátíme do bodu A má ten zelený vektor stále stejný směr.
Tato na první pohled "samozřejmá" trivialitka totiž v zakřivených prostorech neplatí.
Uvažujme opět sféru a tečnou rovinu v bodě A (na severním pólu). Vybereme si v ní nějaký tečný vektor (zelený), naložíme ho na sáňky a vyrazíme na jih. Kam taky jinam. Jenže jakmile kus cesty ujedeme, zjistíme že tečná rovina v novém bodě je jiná (oproti té původní se trochu svažuje) a není apriori jasné jak vektory z té původní roviny identifikovat s vektory v rovině nové. V předchozím případě jsme prostě zachovávali směr zeleného vektoru, ale tady se nám tečná rovina během přenosu neustále naklání (a s ní se naklání i všechny tečné vektory v ní obsažené), takže o nějakém zachování směru nemůže být ani řeči.
V zakřiveném prostoru je tedy nutno paralelní přenos vektorů podél křivek definovat opatrně. Začneme pohybem podél geodetiky. V každém bodě si představíme normálový vektor n k ploše, po které jedeme (něco jako hromosvod přišroubovaný na naše sáňky - to se nám bude hodit při průjezdu bouřkou) a pro rovnoběžný přenos budeme vyžadovat, aby se tečná rovina, naložená na sáňky, kolem tohoto hromosvodu za jízdy neotáčela (myslím tu bleděmodrou rovinu o 4 obrázky výše).
Jinými slovy, pokud táhneme sáňky a naše asistentka v rukou pevně třímá hrábě (zelený vektor), pak při pohybu podél geodetiky provádíme paralelní přenos (přestože absolutní směr hrábí se během cesty mění).
A teď přijde ten háček.
V okamžiku, kdy se vrátíme do bodu A, s hrůzou zjistíme, že náš pečlivě přenášený zelený vektor (hrábě) trčí úplně jiným směrem.
Podívejme se na to. Přesuneme se třeba po sféře z bodu A (severní pól) do bodu B na rovníku, odtamtud podél rovníku (což je geodetika) do jiného bodu C a pak zpátky na sever do bodu A. Já vím, táhnout sáňky po Sahaře není žádný med, ale co by člověk pro rozvoj vědy neudělal.
Samozřejmě v bodě B, kde sáňky pootočíme o 90°, musíme dávat pozor, aby nám asistentka s tím zeleným vektorem nehejbnula (děláme přeci paralelní čili rovnoběžný přenos!). Takže zatímco při pohybu na jih držela hrábě bojovně vpřed, teď je podél rovníku bude muset držet v pravém úhlu ke směru jízdy.
V bodě C opět sáňky otočíme (při čemž nám asistentka drží zelený vektor v konstantní poloze) a vyrazíme zpátky na sever (hrábě tentokrát trčí dozadu). No a v okamžiku, kdy dorazíme zpět do bodu A zjistíme, že náš vektor, který jsme opatrně rovnoběžně přenášeli se od původního vektoru liší o nenulový úhel.
To prosím není žádný logický chyták ani optický klam.
To je charakteristická vlastnost zakřivených prostorů. Při pohybu podél uzavřených křivek se směr "rovnoběžně" transportovaného vektoru změní. A čím je prostor zakřivenější, tím více se cílový vektor odlišuje od toho počátečního.
+++++++++
Možná si říkáte, že je to tím, že naše trajektorie nebyla dostatečně hladká (dvakrát jsme skokově změnili směr jízdy). Třeba nám naše asistentka při obratu sáňek s vektorem trochu "cukla". Ale můžete si obrázek prohlédnout ještě jednou. Necukla.
To posunutí rovnoběžně přenášeného vektoru naměříte i při pohybu podél spojitých křivek, např. podél severního polárního kruhu, kdy směr pohybu měníte pozvolna, takže k žádnému cukání nedochází. Vyrazíte z nějakého bodu a když se do něho vrátíte, rovnoběžně transportovaný vektor trčí trochu jiným směrem (viz tato diskuse). Polární kruh ale není geodetikou a v tomto případě musíme ten rovnoběžný transport definovat trochu jinak.
Ale na to se podíváme až příště.
+++++++++
Neeukleidovské geometrie představují trochu tajuplné hájemství královny věd, protože v nich neplatí "očividné" geometrické zákony, které se učíme ve škole. Jsou tedy v jistém smyslu Divokým Západem matematiky. Proto si v průběhu této minisérie budeme léčit roztřepaná neuronová spojení hudbou ze starých westernů. A zahájíme klasikou nejklasikovatější. Elmer Bernstein: The Magnificent Seven.
Předchozí díly Matykání.
Jan Řeháček
Jaro: das ist nur die erste Phase

Jaro má v našem parku tři fáze, které jsem výstižně pojmenoval: první, druhá a třetí. Toto je svědectví o první z nich. Můžeme s ním nesouhlasit, můžeme proti němu protestovat, ale to je asi tak vše, co s tím můžeme dělat, Járo.
Jan Řeháček
A je po Velikonocích. A nejen po nich.

Globální kotlík zavěšený nad ohněm inkluze a diversity pomalu vytlačuje národní státy, vyrůstající ze sdíleného kulturního podhoubí. Tomuto trendu se nově přizpůsobuje i řada českých svátků s jejichž novelizací vás chci seznámit.
Jan Řeháček
Impresionisté na hladině

Když se na podzim objevily barvy na stromech, všiml jsem si, že se občas zrcadlí v našem potoce či rybníčku. Tak jsem na ně zamířil objektiv a vyšly z toho roztěkané výtvarné kreace, za které by se nemusel stydět ani Claude Monet.
Jan Řeháček
AI Art: co už umí a co ještě ne

Loni jsem trochu experimentoval s malířskými schopnostmi tehdy nastupující generativní AI Art. Letos, za dlouhých zimních večerů jsem si na to vzpomněl a napadlo mne podívat se, jak moc za ten rok AI pokročila. Nu, posuďte sami.
Jan Řeháček
Není větvička jako větvička

Stromy a jejich rozeklaná větvoví jsou sochařská díla. V létě to ale nepoznáte, protože přírodní majstrštyky zakrývá koruna. Jakmile ale podzim povolá svá vojska zpět do zálohy, ladná elegance dřevěných křivek vystoupí do popředí.
| Další články autora |
Nahá umělkyně za zvuků techna házela před dětmi hlínou. Už to řeší policie
Policie prošetřuje vystoupení, ke kterému došlo na Akademii výtvarných umění (AVU). Umělkyně a...
Stovky amerických obrněnců se v řádu dnů nepozorovaně přemístily do Česka
Několik set vozidel americké armády včetně obrněnců Bradley nebo transportérů M113 se objevilo ve...
Německo je otřeseno. Přišel brutální útok na politika, pak následoval další
Na lídra kandidátky německé sociální demokracie (SPD) v Sasku do evropských voleb Matthiase Eckeho...
Auto vyjelo z vozovky a srazilo tři lidi. Žena zemřela, dvě vnučky jsou zraněné
Osobní auto srazilo dnes odpoledne v Čáslavicích na Třebíčsku ženu a dvě děti. Žena srážku...
Vyváděla strašné věci. Zahradil označil Jourovou za nejhorší z eurokomisařů
Premium Když Česko vstoupilo 1. května do Evropské unie, byl tam matador ODS Jan Zahradil kooptován...
Kdo vlastní české firmy. Zahraniční kapitál roste, počet Rusů v čele klesá
Ruský kapitál v českých firmách od invaze na Ukrajinu a s ní spojenými sankcemi klesá, některé...
Měření lebek či nucená převýchova. Sámové podávají svědectví o křivdách
Krádeže území, odebírání dětí na převýchovu nebo pseudovědecké experimenty. To je pouze část...
Záchranka na maratonu ošetřila 52 běžců po kolapsu, do nemocnice museli čtyři
Záchranáři na Pražském mezinárodním maratonu ošetřili 52 běžců, vesměs po kolapsu. Informovali o...
V německém Magdeburgu strhl vichr skákací hrad i s dětmi do Labe
V německém Magdeburgu v neděli poryv větru strhl do Labe skákací hrad, na kterém se bavilo několik...

Chcete, aby vaše děti měli v dospělosti bohatství? Přečtěte si, jak na to!
Správné finanční návyky a dovednosti vznikají právě v dětství. Mnoho dětí je přijímá přirozeně od svých rodičů, kteří jsou pro děti velkým vzorem....
- Počet článků 402
- Celková karma 19,54
- Průměrná čtenost 920x