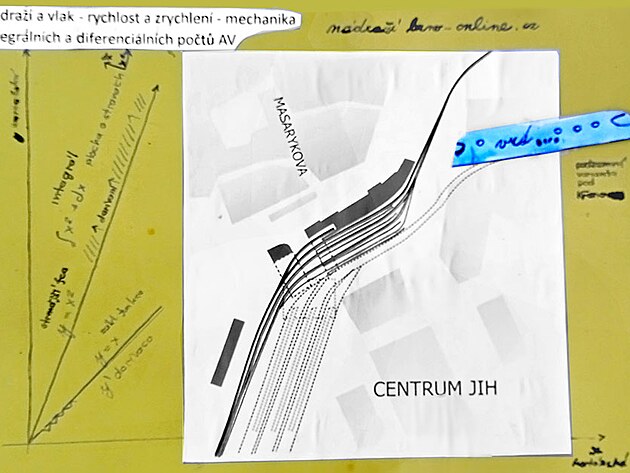
Nádraží a vlak - rychlost a zrychlení - mechanika integrálních a diferenciálních počtů AV

Vlak či jiný pohyb  - a mechanika integrálních a diferenciálních počtů by měly přinést například vzorce pro výpočty pohybu - a to například zrychlení a rychlost vlaku z pozice cestujícího ve vlaku - nebo pozorovatele vně...

 

Nádraží a vlak - rychlost a zrychlení - mechanika integrálních a diferenciálních počtů  AV

Hlavní zkoumanou veličinou je rychlost a poloha vlaku.  Rychlost je definována jako funkce dráhy podle času. Ovšem je jistý zádrhel - že dráha - nebo přesněji délka nejsou proměnné. Jednou z možností jak měnit délku - přesněji dráhu je derivace. Součástí integrálu - který zase vychází z kvadratické funkce je také derivant - jako varianta derivace. Integrál má mimo jiné také význam pro stanovení polohy vlaku - a navigaci. 

OBSAH

rozcestník matematika 

část 1 
rozdíl mezi rovnicí a funkcí - průběh funkce

část 2
integrální a diferenciální počet - obecné pojednání
diferenciální počet
integrální počet

část 3
rozdíl mezi x a y v kartézských souřadnicích, a rozdíl mezi x a y v rovnici (tedy ve funkci) hradlo - vlak - nástupiště

část 4 
přepočty výkon - zrychlení -  rychlost - rozjezd - jak se liší integrál a kvadratická funkce

část 5
poloha vlaku v souřadnicích, rychlost vlaku a "ubíhavost" krajiny"
co  se vlastně počítá, jaký význam má levá a pravá strana v rovnici

část 6 
integrální a diferenciální počet z hlediska pozorovatele
integrální a diferenciální počet jako matematický zápis - z hlediska zobrazení do souřadnic
 integrální a diferenciální počet jako matematický zápis - z hlediska zobrazení do souřadnic
VÝKON hradlo - vlak - nástupiště
JÍZDA
ROZJEZD
DERIVACE - PRŮNĚT JÍZDY 
hodnota rychlosti na ose "X"

část 7
integrální a diferenciální počet z hlediska pozorovatele se zaměřením na rychlost
veličina kterou vnímá služba na hradle je vlastně i n t e g r á l  r y c h l o s t i   
neboli r y c h l o s t  na  d r u h o u (veličina s dvakrát integrovaným časem)
nebo také r y c h l o s t  krát z m ě n a   r y c h l o s t i 

část 8
tři metody výpočtu rychlosti 
výpočet rychlostí jako dvousložkové veličiny (zrychlený pohyb krát rovnoměrný pohyb), výpočet rychlosti dráha lomeno čas) 
rychlost nebo zrychlení (matematika DAV)

rozcestník matematika 

 

matematika a kybernetika 

Ac odkaz na rozcestník matematika a kybernetika  V zajetí počítačů, elektroniky a kybernetiky 4 - Blog iDNES.cz

Ac3 V zajetí počítačů 3 (matematická logika a technika, logická hradla logické funkce) - Blog iDNES.cz

konjukce (logický součin průnik) - hradlo "and"
disjunkce (logický součet) - hradlo "or"
Shefferova spojka (negace logického součinu)  - hradlo "nahd"

matematika

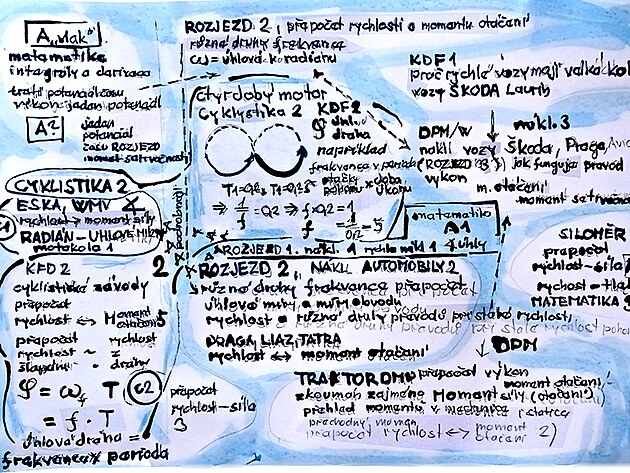
A vstupní příspěvek pro matematiku - se zaměřením na doplňkové výpočty (např. přepočet úlových měr, druhů frekvence) v mechanice pohybu Mechanika A/ KFD : kinematika (frekvence), dynamika (úhlová a obvodová rychlost - Škoda - Blog iDNES.cz

A0 hlavní  příspěvek a rozcestník pro kinematiku, dynamiku a mechanickou matematiku Mechanika A0/ KFD  rozcestník matematická mechanika a jak měří siloměr přes rychlost sílu - Blog iDNES.cz a současně rozcestník VUT Brno

A2 rozjezd nákladních automobilů 2 Mechanika DPM 2/W čím se liší veličiny tlak - síla a práce? - nákl. vozy Škoda/Praga - Blog iDNES.cz automobilka Praga - Praha Libeň horní nádraží

A3 různé druhy frekvence podrobněji a současně příspěvek nákladní automobily 3 (rychlá nákladní vozidla, sanitky), či rozjezd vozidel 3 Mechanika A1/KFD - rychlá nákladní vozidla a jejich rozjezd (1) přepočty druhů frekvence - Blog iDNES.cz

AS integrální a diferenciální počet  slovesně "AS" Matematika a mechanika slovesně - aneb jak se vaří bramborový guláš - Blog iDNES.cz

AV integrální a diferenciální počet  Nádraží a vlak - rychlost a zrychlení - mechanika integrálních a diferenciálních počtů "AV" - tento příspěvek

A11V integrální a diferenciální počet (II) a Eulerova konstanta Eulerova konstanta (Co se děje kolem matematiky, fyziky a elektrotechniky 11) - Blog iDNES.cz

matematická logika a úvahy

pravé a nepravé dělení (porcování či krájení a poměřování) je předmětem třeba příspěvku

As Matematické úvahy u sázení brambor - Blog iDNES.cz hlavní příspěvek pro matematické úvahy typu sudá a lichá funkce, nepravé a pravé dělení 

A4s pravé a nepravé dělení (porcování a poměřování) Mechanika DAV(PM): Holešov - rychlost letounu Z 142 - okamžitá a statistická ,zrychlení - Blog iDNES.cz

Mechanika A/ DAV (PM) - rychlost a zrychlení - veličina "čas" jako dělitel - Blog iDNES.cz příspěvek se zabývá především analýzou dělitele jako matematického operátoru a kdy vzniká "pravé" a "nepravé" dělení

Mechanika - elektrotechnika MFE 5 - výkon - jako moment třetího stupně, kruhový diagram - Blog iDNES.cz  v původním příspěvku rovněž pojednáno pravé a nepravé dělení 

matematika - úhly a míry, goniometrické funkce

aritmetická geometrie   převody úhlů (Ludolfovo číslo, radián) - přepočty mezi různými druhy frekvencí (úhlová frekvence k radiánu, frekvence k celému úhlu, RPM  otáčky za minutu)  v  rámci příspěvků

(tři příspěvky zabývající se obdobným tématem - tedy přepočty matematických veličin a vzorců - které se uplatňují v mechanice pohybu - ve spojení s nějakým dalším tématem mechaniky pohybu - tedy kinematiky a dynamiky)

POMĚR MEZI OBVODEM KRUŽNICE jako východisko pro další přepočty - Ludolfovo číslo a rozměr úhlu jeden RADIÁN

tři příspěvky zabývající se obdobným tématem - tedy přepočty matematických veličin a vzorců - které se uplatňují v mechanice pohybu - ve spojení s nějakým dalším tématem mechaniky pohybu - tedy kinematiky a dynamiky

A Mechanika A/ KFD - Ludolfovo číslo a radián - přepočty různých druhů frekvence - Blog iDNES.cz mechanika a matematika v automobilismu - opravna vozů Škoda Jihlava

A3 Mechanika A1/KFD - rychlá nákladní vozidla (sanitky) a jejich rozjezd (1) přepočty druhů frekvence - Blog iDNES.cz  oblouková míra - stupně, Ludolfovo číslo a radiány (výkon a točivý moment 3), dále přepočet vstupní a výstupní rychlosti, který tvoří dvopříspěvek jako (1) s příspěvkem 

AV11 Eulerova konstanta (Co se děje kolem matematiky, fyziky a elektrotechniky 11) - Blog iDNES.cz

Oblouková míra - stupně, Ludolfovo číslo a radiány a přepočet rychlosti vstup - výstup - Blog iDNES.cz součástí příspěvku alternativní výpočet rychlosti z frekvence nebo dráhy

goniometrické funkce pak v příspěvcích 

V cirkuse, Brněnský Prátr, jak vypočítat a postavit stan - Blog iDNES.cz

Mosty od klenbových po vysuté (statika 2) - soustava staticky (ne, pře) určitá - Blog iDNES.cz

vnitřní matematika – matematika přepočtů

	Mechanika A0/ KFD  rozcestník matematická mechanika a jak měří siloměr přes rychlost sílu - Blog iDNES.cz
	Mechanika A/ KFD : kinematika (frekvence), dynamika (úhlová a obvodová rychlost) - Škoda - Blog iDNES.cz
A11V	A11V Eulerova konstanta, integrály a derivace (Co se děje kolem matematiky 11) - Blog iDNES.cz
AVC	Eden, Afrika, V cirkuse, Brněnský Prátr - jak vypočítat a postavit stan - Blog iDNES.cz
A3Avia“radiánfrekvence	Mechanika A1/KFD - radián, druhy frekvence, rozjezd a výkon sanitky - Blog iDNES.cz
C1přepočtyúhlů,––,,	C1 Mechanika A/DPMW: stupně, Ludolfovo číslo radiány - přepočet rychlosti, značky bicyklů - Blog iDNES.cz

vnější matematika – matematické funkce (i pro jiné obory)

	A11V Eulerova konstanta, integrály a derivace (Co se děje kolem matematiky 11) - Blog iDNES.cz
AV
AVEelektrotechnika)	Co se děje kolem elektřiny 7 - Ohmův zákon (2) a matematická funkce, osciloskop, FE VUT - Blog iDNES.czCesty elektrické energie a Ohmův zákon 2 - elektrárna Oslavany, Západomoravské elektrárny - Blog iDNES.cz
AK	Hallův efekt, matematika kosmických letů ; autoelektrika a elektromobil - Blog iDNES.cz
	"AVs" Matematická zamyšlení aneb jak se sází brambory a vaří bramborový guláš - Blog iDNES.cz

Co se děje kolem elektřiny 7 - Ohmův zákon (3) pro zapojený obvod - funkce a integrál, osciloskop - Blog iDNES.cz rovněž zahrnuje integrální a diferenciální počet

vlastní příspěvek 

část 1 rozdíl mezi rovnicí a funkcí - průběh funkce 

"část 1" příspěvku je podrobněji pojednána v příspěvku A11V Rovnice, funkce, derivace, logaritmy a Eulerova konstanta - Blog iDNES.cz

Jaký je vlastně rozdíl mezi levou a pravou rovnice a rovnicí, funkcí a veličinou?

informační poznámka - obvyklý zápis rovnice je 

funkce  : Y (řídící neznámá) =X (výkonná neznámá)na entou

funkce  : Y =X na entou

dále v textu však poměrně často použito přehozené x a y 

tedy

funkce  : Y = X

 na entou

rovnice sice není přímo funkce, ale v mnoha případech rovnice a funkce může být totéž

nejprve rovnice -  ovšem s levo - pravým dělením podle stran již jako funkce

Co je to vlastně vyjadřuje rovnice... Na vzdory rovnítka uprostřed neznamená, že levá a pravá strana rovnice vyjadřuje totéž. 

LEVÁ STRANA ROVNICE - souhrnná neznámá "Y" (funkce, zjišťovaný pochod) - PRAVÁ STRANA ROVNICE spíš prostředek výpočtu,(zkoumaná veličina, konkrétní výsledek).- výkonná neznámá "x", případně "z" 

LEVÁ STRANA ROVNICE (rychlost) - PRAVÁ STRANA ROVNICE spíš prostředek výpočtu, (zkoumaná veličina - dráha, funkce času). 

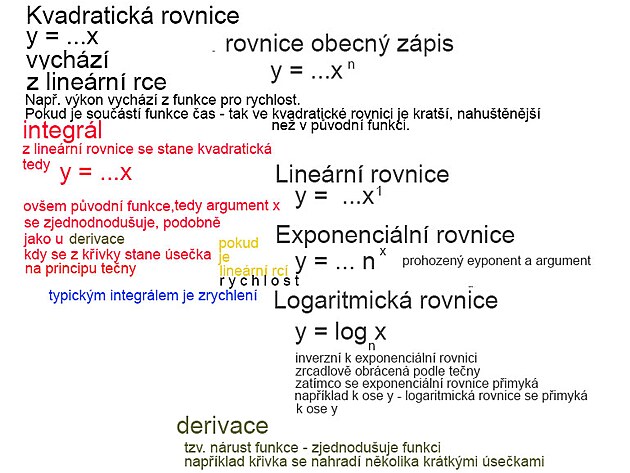
druhy rovnic a funkcí 

lineární rovnice s jednou neznámou a to na prvou
kvadratická rovnice - s neznámou - což je zpravidla x na druhou
funkce s x na druhou - teoreticky by se mělo jednat o kvadratickou funkci (toto označení se ale příliš nepoužívá) - pro tuto funkci se zde v příspěvcích používá i nepřesně označení exponenciální funkce 
exponenciální rovnice - s neznámou v exponentu 
logaritmická rovnice - teoreticky by byla příbuzná s exponenciální rovnicí - převrácená exponenciální rovnice
goniometrická rovnice - která zahrnuje funkce sinus a cosinus 

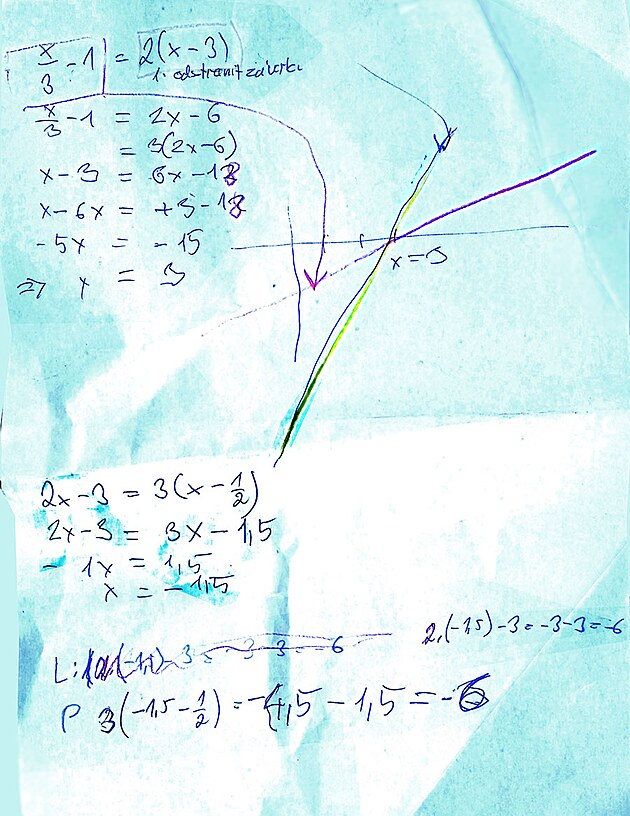
průběh rovnic 

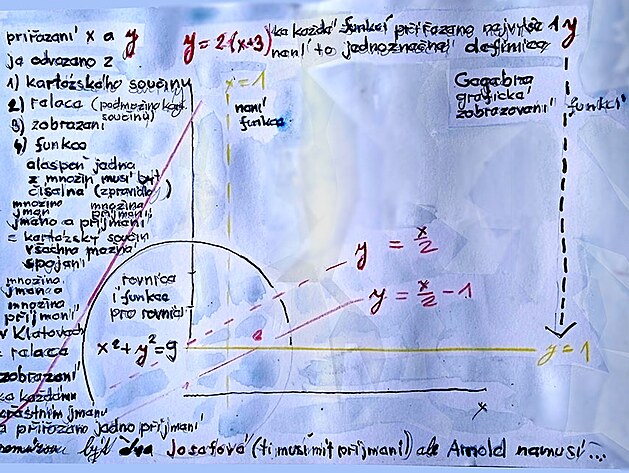
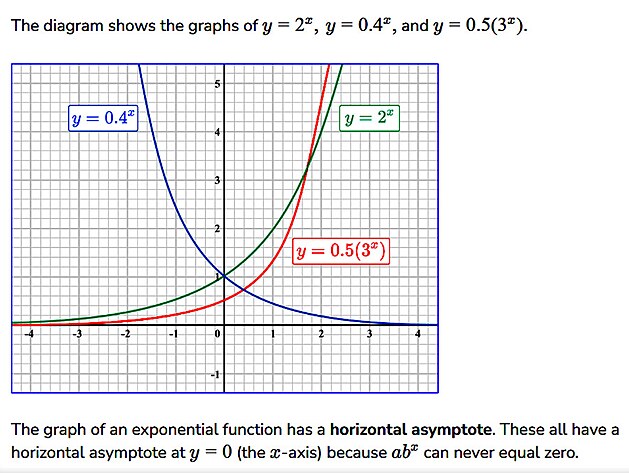
na obrázku níže zobrazeny

žlutě: rovnice x = 1, která by stoupala strmě podél osy y, a pak funkce y = 1, jejíž průběh by byl podél osy x  

červeně: funkce y = x/2 a funkce y = x/2 - 1 obě funkce směřují v úhlu 45st. mezi osami a druhá zmíněná funkce je o jednotku na stupnici posunutá 

dále je zde uvedena kružnice - která je definována vzorcem x na druhou + y na druhou = 9

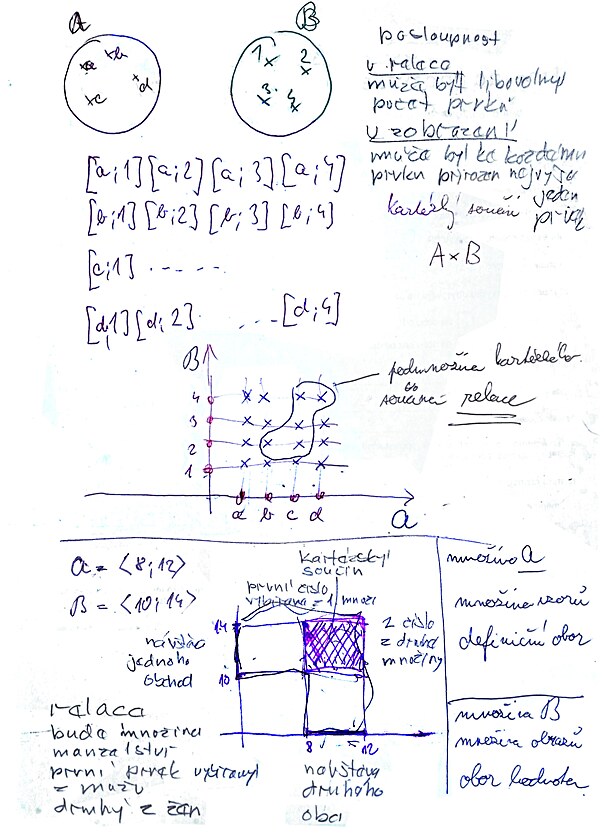
Funkce a příbuzné matematické záležitosti mohou mít jednak číselný (matematický) zápis - dále jdou zobrazit graficky - a rovněž zpravidla mají nějaký reálný význam - mohou popisovat průběh elektrotechnických veličin - veličin v mechanice - jako například průběh rychlosti  - dále mohou popisovat úplně běžné záležitosti - různé přiřazování souvisejících veličin různých druhů...

Kromě funkce se v matematice vyskytuje řada souvisejících záležitostí (viz tabuka níže), které mezi sebou souvisí a vytváří různé podmnožiny...

relace
/funkce

průběh funkcí 

průběhy funkcí 

druhy rovnic a funkcí a jejich průběh  

lineární rovnice s jednou neznámou a to na prvou
kvadratická rovnice - s neznámou - což je zpravidla x na druhou
funkce s x na druhou - teoreticky by se mělo jednat o kvadratickou funkci (toto označení se ale příliš nepoužívá) - pro tuto funkci se zde v příspěvcích používá i nepřesně označení exponenciální funkce 
exponenciální rovnice - s neznámou v exponentu 
logaritmická rovnice - teoreticky by byla příbuzná s exponenciální rovnicí
goniometrická rovnice - která zahrnuje funkce sinus a cosinus

zajímavá věc - exponenciální a kvadratická funkce - přesněji jich grafický průběh - se poměrně podobají

 

malé pojednání o funkcích a veličinách

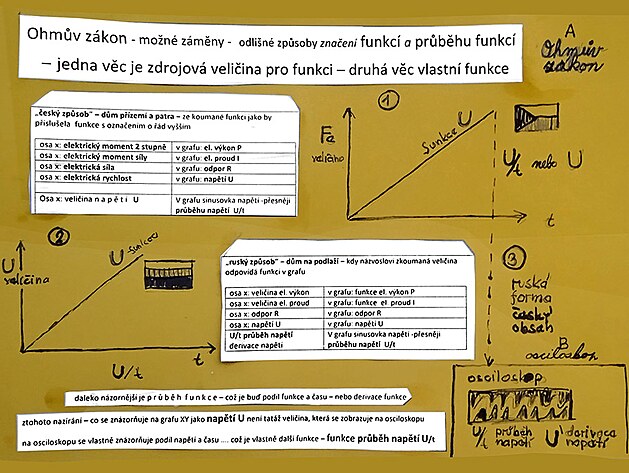
třeba už z názvosloví při značení funkcí mohou vznikat jisté nejasnosti

něco jiného je zdrojová veličina na ose y - a něco jiného je zjišťovaná funkce v grafu

Co je to vlastně vyjadřuje rovnice... Na vzdory rovnítka uprostřed neznamená, že levá a pravá strana rovnice vyjadřuje totéž. 

LEVÁ STRANA ROVNICE - souhrnná neznámá "Y" (funkce, zjišťovaný pochod) - PRAVÁ STRANA ROVNICE spíš prostředek výpočtu,(zkoumaná veličina, konkrétní výsledek).- výkonná neznámá "x", případně "z" 

LEVÁ STRANA ROVNICE (rychlost) - PRAVÁ STRANA ROVNICE spíš prostředek výpočtu, (zkoumaná veličina - dráha, funkce času). 

poměrně důležitý pojmem je také 

LICHÁ a SUDÁ funkce

pojmy LICHÁ (neúplná funkce - pouze s y)  a SUDÁ funkce (plnohodnotná funkce - s y i x)

poměrně připomínají zde pracovně, či studijně zavedené pojmy

NEPRAVÉ DĚLENÍ (něco jako poměr mezi pruhy na vlajce, poměřování )

Veličina čas zde ČAS jako NEPRAVÝ DĚLITEL - KVALITIFIKÁTOR (matematická operace dělení zde ve smyslu ZMĚNA - podobající se chemickým reakcím při vytváření nových látek) .

PRAVÉ DĚLENÍ (něco jako porcování dortu)

(DVA druhy operandů ČASu při přepočtech mezi odlišnými druhy fyzikálních MOMENTů)

odkaz na původní příspěvek kde je zkoumáno "pravé a nepravé" dělení - a dva časy ve výpočtech -- jeden při ose y, druhý při ose X....

Mechanika DAV(PM): Holešov - rychlost letounu Z 142 - okamžitá a statistická ,zrychlení - Blog iDNES.cz

 

...dále již pokračování předchozích úvah o funkcích a rovnicích ....

ostatně z důvodů dvou různých 

Y = X na n ou

v případě rychlosti

rychlost = dráha (jako funkce času) / lomeno čas

v grafu kartézských souřadnic je  funkce poněkud jinak než v rovnici - pokud by se i rovnice zobrazila graficky - viz další část

rychlost (probíhá  v meziose xy) =dráha (jako funkce času)  - se zase odečítá na ose Y LOMENO čas(se zase odečítá na ose X

možná ještě názornější by posun v označení, případně názvosloví více vyjadřující podstatu veličiny by byl u veličiny rychlost 

možná by bylo názornější, když by veličina měla stejné značení jako funkce 

(na obrázku níže místo rychlosti elektrické napětí)

podle zde pracovně  zavedeného ruského názvosloví, kdy se domy číslují na podlaží bez přízemí, by název pro rychlost mohl znít 

"ruský způsob značení" - kdy se domy nečíslují na patra - ale podlaží a číslování vlastně začíná prvním podlažím

tedy veličině napětí U (zobrazované na ose y) odpovídá funkce napětí U (kolem meziosy xy)

jiný způsob značení by byl

"český způsob značení" - kdy číslování začíná přízemím a teprve další podlaží se nazývá první patro

tedy veličině elektrický výkon P (na ose Y) odpovídá funkce napětí U (kolem mezioy XY)

k obrázku výše "český a ruský způsob značení jisté vysvětlení" - v případě "českého"  značení by na ose Y měl být výkon (U=RP) neboli napětí jako funkce výkonu, v případě tzv "ruského" značené (U=U)

shrnuto

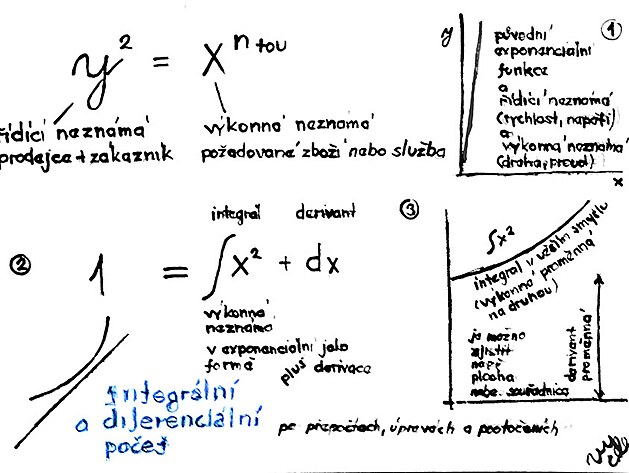
exponenciální  funkce nebo integrál : Y na druhou = X na entou

funkce  : Y = X na entou

derivace.Ys apostrofem =  n(tedy nárust funkce - neboli přímka)

z jednotlivých krátkých úseků "nárustů" funkce - se dá ovšem poskládat původní funkce (přesněji obrazec funkce, napodobenina funkce - křivka která se zobrazuje vlastně na osciloskopu)

část 2
integrální a diferenciální počet - obecné pojednání

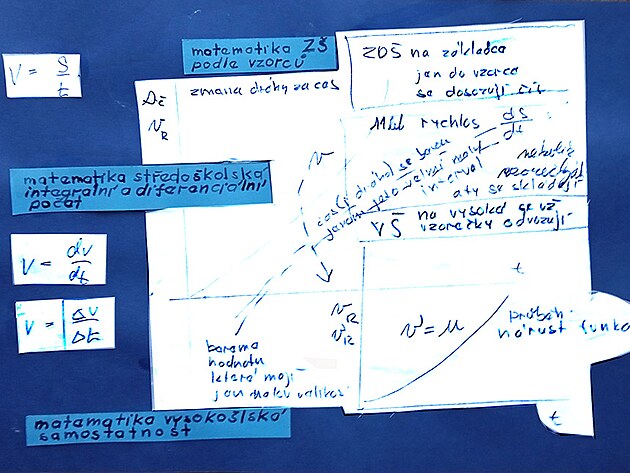
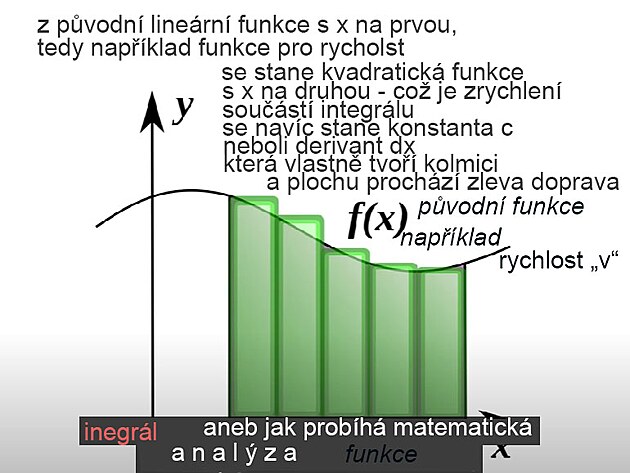
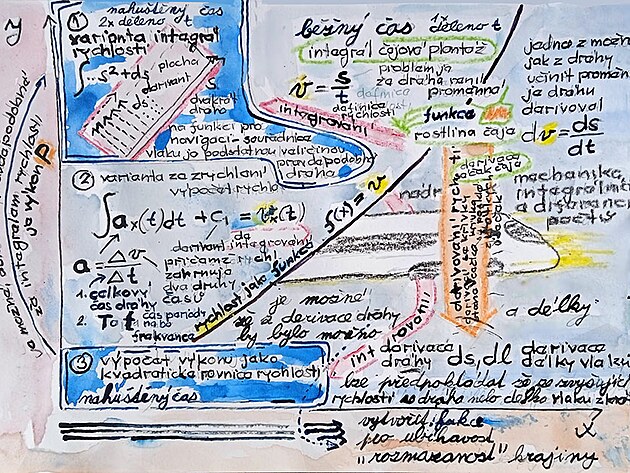
Pokud by se porovnal integrál - výchozí funkce - derivace - pak by mohl být na místě příměr "čajová plantáž" jako integrál, rostlina čaje jako výchozí funkce - a sáček z čajem jako derivace. Čistě procesně - integrování a derivování se podobá - v obou případech se křivka nahrazuje úsečkou (která vychází z tečny k původní přímce). Zatímco v případě derivace se křivka zjednoduší - "obalí" - krátkými úsečkami - v případě integrování se původní křivka také zjednoduší - nahradí úsečkami - jenomže z lineární rovnice, či funkce se stane funkce vyššího řádu - která vychází z kvadratické rovnice - tedy se zvýší exponent z "na prvou" na exponent "na druhou" - tedy na místo jedné tečny - jako v případě derivace - tak v případě integrálu vlastně vznikne dvojice tečen - a mezi nimi plocha. Tuto plochu z boku vymezuje konstanta "c" - nazývaný také jako derivant (snad z důvodu, že integrování se procesně podobá derivování) - a tato kolmice - neboli rozteč integrálu vpodstatě prochází plochu integrálu z jednoho kraje na druhý - a na tomto principu funguje například zjišťování polohy vlaku. 

Co je to vlastně vyjadřuje rovnice... Na vzdory rovnítka uprostřed neznamená, že levá a pravá strana rovnice vyjadřuje totéž. 

LEVÁ STRANA (mohla by znamenat výsledek - řídící neznámou -, ale spíš vychází jako prostředek)

PRAVÁ STRANA rovnice obnáší nějaký pochod, FUNKCI, která zahrnuje skutečný VÝSLEDEK nějakého úsilí, výkonnou neznámou. 

Řídící neznámá j- na levé straně rovnice - je zpravidla označována jako "Y" - výkonná neznámá zase jako "X" - dále v textu je poměrně často použito opačné označení - pro levou stranu "x" - pro pravou stranu "y".

Integrály nebo derivace nevytváří z původní funkce funkci vyššího ani nižšího řádu - pouze funkci upravují - aby se dalo zjistit například co daná funkce neumí (týká se to zejména integrálu) - nebo se funkce zjednodušila tak - aby se například neznámá vyskytovala nikoliv i v čitateli a zároveň jmenovateli zlomku - ale například jenom ve jmenovateli (v případě derivace). 

Zjednodušeně lze shrnou - že derivace má podobný význam jako "Eulerova konstanta" - zatímco Eulerova konstanta zjednodušuje například trojúhelník na čtverec - derivace zjednodušuje parabolu na polopřímku. V kartézských souřadnicích také původní funkce i její derivace jsou umístěny přibližně ve stejných souřadnicích... 

Například v případě definičního vzorce pro rychlost, tedy rychlost rovná se dráha lomeno čas, vlastním výsledkem je obvykle dráha (tedy přemístění z místa A do místa B( než rychlost - ta spíš vychází jako prostředek. 

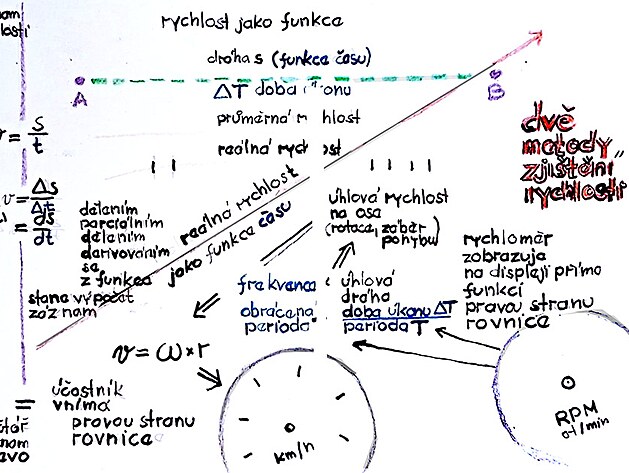
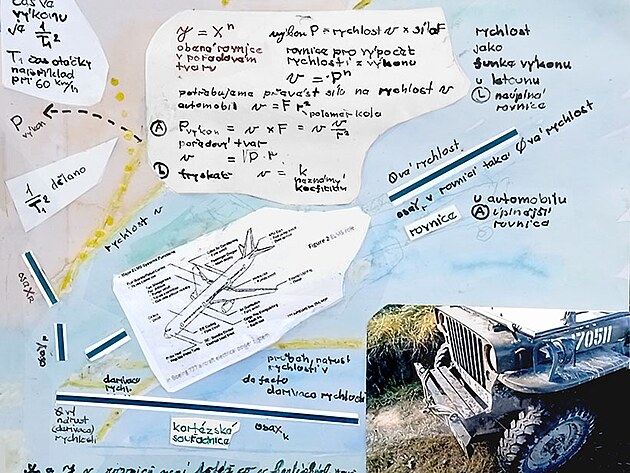
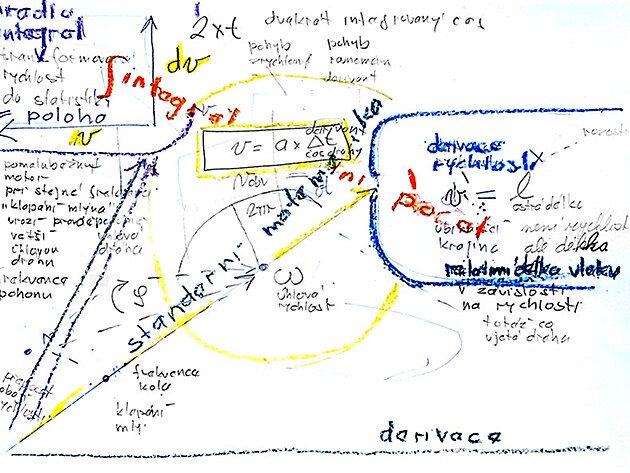
Na obrázku výše jsou jednak dvě metody zjišťování rychlosti (tedy jednak definiční metoda dráha lomeno čas, a druhá metoda přepočtem z frekvence,či otáček,  na jaké jsou pravděpodobně založeny i měření rychlosti ve vozidlech. 

Na výše uvedeném obrázku jsou ještě další informace  a to pás vlevo, nazvaný jako záznam rychlosti - a plocha na pravo - která popisuje vlastní funkci pro výpočet rychlosti (nebo možná ještě přesněji - funkci pro uskutečnění například nějaké přepravy po stanovené dráze).

Vzhledem k faktu, že rychlost obvykle vytváří nějakou křivku - není zcela matematicky snadné vypočítat rychlost z celé dráhy, protože se rychlost různě liší...

Proto je pás vlevo označen jako záznam rychlosti, kde se liší jen různé metody výpočtu rychlosti (průměrná rychlost z celé dráhy a souhrnného času, parciální podíl, derivace). Derivace rychlosti neznamená nic jiného, než přesnější výpočet rychlosti než jinou metodou. 

Derivaci,  onomu symbolu doplněným čárkou, by v případě rychlosti spíš než označení derivace rychlosti lépe příslušelo označení výpočet rychlosti derivací.  

diferenciální počet

Co je to vlastně derivace, případně integrál?
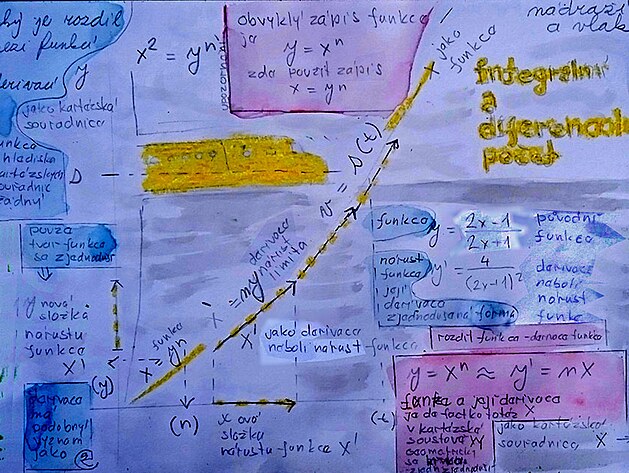
Jedním z mnoha vysvětlení by bylo, že derivace vlastně nepopisuje přesnou funkci, ale zjednodušuje ji  na nárust funkce - nebo jak je například křivka v konkrétním místě strmá. Nebo také, že zjednodušuje křivku na přímku - s určitou orientací v kartézských souřadnicích. 

V kartézských souřadnicích "x-y" je tedy funkce  - de facto totéž jako její derivace - přibližně kolem mezi osy xy - jenom místo křivky - např.y = x na ntou -- třeba paraboly se vytvoří zjednodušená funkce y´ = n krát x ,  a například z krátkých úseček poskládaných z přímek derivací lze poskládat téměř původní funkci - její napodobeninu.

Derivováním se například z křivky vytvoří přímka (spíš úsečka) která se zobrazí do osy Y jako tzv. nárust funkce - následně se pootočí tak, že vytvoří tečnu původní křivky.

Z krátkých úseček - derivací funkce - se řekněme "obalí" původní funkce - a tím vznikne něco jako napodobenina původní funkce.

Rychlost  je jedna funkce - a co se zjišťuje výpočtem – podobně jako se znázorňuje na osciloskopu jako napěti vlastně není napětí - ale nárust napětí (funkce "nárust napětí") -  tedy v podstatě napětí vydělené  časem/ - v případě vlaku z matematického hlediska nárust rychlosti - což je vlastně samostatná nárust rychlosti – a jednotlivých funkcí „nárust rychlosti“ by se vlastně měla dát poskládat reálná rychlost – čímž by se z definičního  vzorce pro rychlost – dráho lomeno čas – měla dát poskládat průběh rychlosti podobně – jako přímým měřením rychlosti tachometrem – který ovšem funguje na jiném principu, a vychází z frekvence pohybu…

Integrál - zase do funkce začleňuje určitý přesah nějakého dalšího úkonu - řekněme do plochy přidává nějaký další rozměr. A takto integrál může podat informaci nejenom o rychlosti vlaku, ale i o jeho poloze...

integrální počet

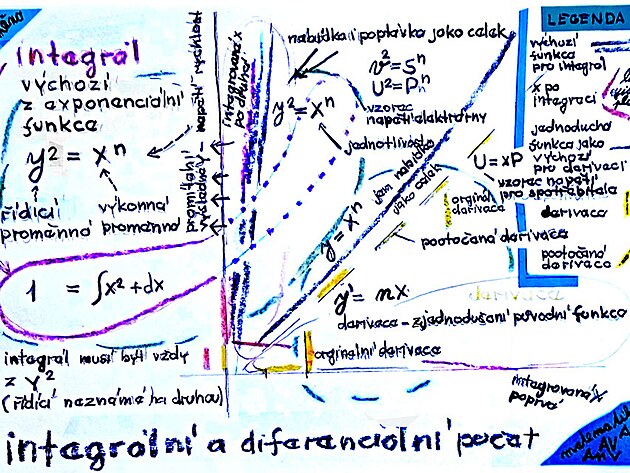
Co se týče integrování - podle daných poznatků integrální počet vychází z kvadratické funkce pro řídící neznámou (tedy y na druhou) - na levé rovnice,  a cílem integrování by podle všeho mělo být zjistit více informací a parametrů pro výkonnou neznámou na pravé straně rovnice. 

V případě integrování se původní křivka zjednoduší podobně jako v případě derivace  - nahradí úsečkami - jenomže z lineární rovnice, či funkce se stane funkce vyššího řádu - která vychází z kvadratické rovnice - tedy se zvýší exponent z "na prvou" na exponent "na druhou" - tedy na místo jedné tečny - jako v případě derivace - tak v případě integrálu vlastně vznikne dvojice tečen - a mezi nimi plocha. Tuto plochu z boku vymezuje konstanta "c" - nazývaný také jako derivant (snad z důvodu, že integrování se procesně podobá derivování) - a tato kolmice - neboli rozteč integrálu vpodstatě prochází plochu integrálu z jednoho kraje na druhý - a na tomto principu funguje například zjišťování polohy vlaku. 

y na druhou (řídící neznámá) = x na n tou (výkonná neznámá)

Přičemž integrování je něco jako systém matematických operací, kterým se získává více informací o pravé straně rovnice s výkonnou neznámou (tedy X).

Levá strana rovnice s "Y" se nahradí hodnotou "1" ke které se srovnává pravá strana rovnice (v integrovaném tvaru).

Rovnicí o dvou řídících neznámých může být definováno například napětí z elektrárny do sítě - nastavené podle spotřeby - jednou by tatáž veličina "y" měla jakoby zastupovat zároveň prodejce a zároveň zákazníka.

Integrální počet by se ovšem měl zabývat pravou stanou rovnice - tedy výkonnou neznámou "x" - což v případě elektřiny buď může být buď výkon spotřebiče - nebo elektrický proud.

Integrál v zásadě zase není nic jiného než variace exponenciální funkce...

y na druhou = x na n tou 

Co se týče integrování - podle daných poznatků integrální počet vychází z exponenciální funkce pro řídící neznámou (tedy y na druhou) - na levé rovnice,  a cílem integrování by podle všeho mělo být zjistit více informací a parametrů pro výkonnou neznámou na pravé straně rovnice. 

Rovnicí o dvou neznámých může být definováno například napětí z elektrárny do sítě - nastavené podle spotřeby - jednou by tatáž veličina "y" měla jakoby zastupovat zároveň prodejce a zároveň zákazníka.

Integrální počet by se ovšem měl zabývat pravou stanou rovnice - tedy výkonnou neznámou "x" - což v případě elektřiny buď může být buď výkon spotřebiče - nebo elektrický proud.

Integrováním by se mělo o pravé straně rovnice zjistit víc, než vychází z výchozí rovnice.

Integrování jakoby se pravá strana rovnice rozdělila na několik funkcí - přesněji řadu funkcí - od nejsložitější po nejjednodušší.

Integrováním jakoby se původní funkce z pravé strany rovnice - s jistým zjednodušením rozdělila například na x na druhou a na x na pravou.

A ze dvou jednodušších funkcí se dá zjistit více než z jedné funkce vyššího řádu. Dá se například vypočítat plocha - dají se například zjistit souřadnice.

část 3
rozdíl mezi x a y v kartézských souřadnicích, a rozdíl mezi x a y v rovnici (tedy ve funkci) hradlo - vlak - nástupiště

o d k a z na podrobnější zkoumání funkcí - integrální a diferenciální počet (II) a Eulerova konstanta, Ludolfovo číslo -  Eulerova konstanta, lichá - tedy neúplná funkce, pravá funkce, exponenciální funkce a její derivace, exponenciální funkce a logaritmická funkce, dvojnásobná exponenciální funkce a integrál A11V Eulerova konstanta, Ludolfovo číslo, integrály, derivace, logaritmy (Co se děje kolem matematiky 11) - Blog iDNES.cz

paralelou integrálních a diferenciálních počtů a různých činností (návod /derivace/ - sázení, sklízení, vaření /funkce/ - a /inegrál/  jako hotový oběd) se zase zabývá příspěvek Matematické úvahy u sázení brambor - Blog iDNES.cz

rozdíl mezi xa y v kartézských souřadnicích, a rozdíl mezi x a y v rovnici (tedy ve funkci)

kde se zkoumaná veličina zapisuje v rovnici - a kde se zobrazuje a načítá v grafu (kartézských souřadnicích)

zápis rovnice Y = X na ntou

v případě elektřiny  U = P na ntou (zjednodušená rovnice pro napětí v síti)

v exponenciálním tvaru U na druhou = P na ntou (je li zkoumán výkon elektrárny)

zpravidla není totožný se zobrazením v kartézských souřadnicích (tedy grafu xy, případně xyz)

v kartézských souřadnicích se obvykle porovnává průběh jedné složky funkce - zpravidla  y a porovnává se s obvykle s časem t

v kartézských souřadnicích by se tedy osa x vlastně klidně mohla jmenovat jako osa t 

v rovnici - neboli funkci se zase porovnávají dvě složky mezi sebou - tedy zpravidla  y  a x 

pokud by se rovnice (funkce) znázornila graficky -x a y by pravděpodobně měly jiný průběh než kartézských souřadnicích - jednak by bylo x a y naopak - a jednak by byl celý graf pootočen asi o 45 stupňů v protisměru hodin

která veličina je x a která je y 

v rovnici či funkci

jako y se zpravidla označuje zkoumaná veličina - tedy například rychlost  v nebo napětí U- jako x se zpravidla označuje výkonnostní veličina - - tedy například výkon P 

v kartézských souřadnicích

zkoumaná veličina (jedna složka funkce) - tedy například rychlost  v nebo napětí U se promítá na osu y (či přesněji načítá na této ose) a sleduje se její průběh v čase (nikoliv porovnává s druhou - výkonnou složkou funkce) - dale by se také říci, že se se v kartézských souřadnicích zkoumá nárust funkce (což by ovšem jako termín úplně přesné nebylo) - neboť takto je vlastně definována derivace (jako nárust funkce) - jinak derivace je vlastně také funkce - jenom zjednodušená - netvoří křivku - ale křivka se rozkládá do krátkých kolmých úseků - jejímž spojením vznikne téměř původní křivka

část 4 

přepočty výkon - zrychlení- rychlost- rozjezd - jak se liší integrál a kvadratická funkce

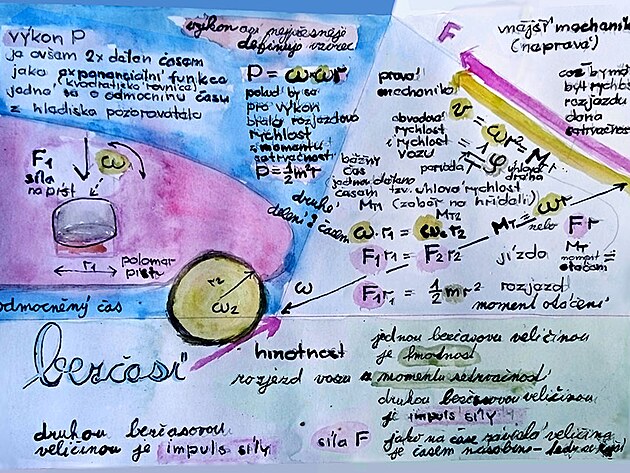
Malé upozornění - hlavním zkoumaným subjektem tohoto příspěvku není veličina výkon - hlavní zkoumanou veličinou je zde rychlost - která vychází z lineárního pohybu celého vlaku. Výkon sice také vychází z rychlosti - ovšem nikoliv celého vlaku - ale pohonu, přesněji rotačního pohybu motoru. Asi nejvýstižnější metodou jak stanovit výkon ovšem není dobře známá obvodová či lineární rychlost označovaná zkratkou "v" - ale tzv. úhlová rychlost OMEGA na ose hřídele motoru - což je vlastně neúpná rychlost - něco jako frekvence se záběrem. Tedy veličina výkon je zde uvedena spíše pro doplněnění - a také rozlišení - či odlišení od ostatních veličin. 

výpočty rychlosti podle druhu pohonu

výkon P je poněkud zjednodušeně  rychlost v  krát síla F

rychlost v a síla F  jsou veličiny které lze vzájemně přepočítat 

z čehož vychází, že výkon lze například vypočítat pouze přepočtem z rychlosti

Jak se liší integrál a kvadratická funkce (či rovnice)?

V nákresu níže jsou  jisté nepřesnosti - zejména jsou zde sloučeny pojmy kvadratická funkce a integrál - víc než odpovídá poznatkům -  i když se v jistém smyslu obě funkce  podobají - v případě  integrálu se výchozí lineární funkce zjednoduší z křivky na tečnu. Součástí integrálu je ovšem navíc konstanta "c" označovaná také jako derivant. Pokud by se porovnávala novofunkce - a původní lineární funkce - pak by vycházely dvojice /kvadratická dvojice výkon - lineární dvojice rychlost, integrální funkce zrychlení - lineární rovnice rychlost.

(novofunkce)	"v
a(novofunkce)	rychlostv

Pvýkon = OMEGA úhlová rychlost na ose  (na druhou - jednou za rychlost, jednou za sílu) x r (poloměr) 

výše uvedený vzorec pro výkon je asi nejvíc vystihující tuto veličinu

níže pokus o přepočet výkonu z veličiny obvodová (což je současně) o lineární rychlost celého vozu 

Pvýkon = v rychlost na druhou lomeno  r (poloměr kola) na třetí 

princip výpočtů spočívá v přepočtu síly přes páku na osu - hřídel - kde má sídlo úhlová rychlost omega (což je vlastně odmocnina síly) - a z úhlová rychlost neboli rotace na hřídeli je přepočítávána na další veličiny  - zejména obvodová rychlost a moment otáčení / síly

a konečně upřesněný vzorec pro výkon na principu výkon = rychlost x síla by zněl

Pvýkon = ODMOCNINA (Fsíla na obvodu kola  x r poloměr kola) x (rychlost v lomeno poloměr r)

Zatímco moment otáčení z hlediska rytmu má tutéž frekvenci jako rychlost anebo frekvence  (klapání mlýna) -výkon P  je dělen časem na druhou - z tohoto hlediska pokud by moment otáčení měl frekvenci deset otáček za vteřinu - což také odpovídá realitě - pomyslnému klapání mlýna - výkon by měl z matematického hlediska frekvenci sto otáček na druhou - vysvětlení? zatímco moment otáčení vychází z běžné matematické funkce y=x(na n-tou) -

Pvýkon  vychází z kvadratické funkce y na n-tou= x (na n-tou).

přepočty výkon, síla, rychlost automobilu se zabývají například příspěvky DPM například  Mechanika DPM1 - Výkon, nebo točivý moment - proč má traktor velké zadní kolo a je pomalý? - Blog iDNES.cz, nebo Mechanika A3/ KFD 3 rozcestník matematika/kinematika - jak měří siloměr přes rychlost sílu - Blog iDNES.cz

o přepočtu výkon, síla, rychlost u proudových motorů by zase měly pojednávat příspěvky Jak měří letecký tachometr rychlost letounu 2, letiště Žatec a Mig 29, mechanika DPMW - Blog iDNES.cz a Aero továrna na letadla / kompozity - konstrukční materiál pro letectví a kosmonautiku - Blog iDNES.cz a zejména příspěvek V rakouské pustě, Letiště Vídeň - Schwechat a letoun Boeing 707 / 737 / 777 - Blog iDNES.cz

 

část 5

poloha vlaku v souřadnicích, rychlost vlaku a "ubíhavost" krajiny"
co  se vlastně počítá, jaký význam má levá a pravá strana v rovnici

 

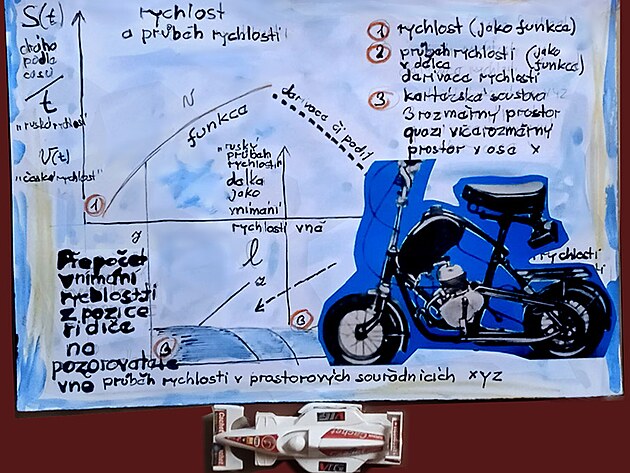
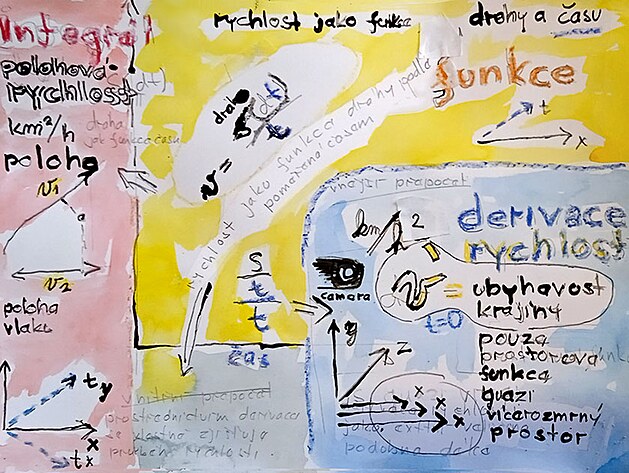
Co vnímá pozorovatel vně, jako ubíhající krajinu - podle všeho vlastně vypočtená rychlost - což je něco jako "rozmazaná délka" - podobně je tomu s napětím odečítaném na osciloskopu - kde je napětí znázorněno jako  geometrický obrazec,  což by při matematickém zápisu znamenalo levou stranu rovnice, zatímco uvnitř monitorovaného elektrotechnického  zařízení probíhá funkce (z matematického hlediska, z elektrotechnického hlediska je obvod pod napětím) - podobně i cestující ve vlaku - alespoň z matematického hlediska by jakoby vnímal pravou stranu rovnice, tedy matematickou funkci.

 

pokud například bereme počítáme rychlost je vlastní funkce "x"- zde konkrétně  tedy "v"  v rovnici na levé straně, v případě grafu je funkce rychlost nikoli na ose x - ale v prostoru meziosy "xy"

ovšem v grafu se rychlost "v" se odečítá na ose y zatímco na ose x se odečítá dejme tomu čas trvání jízdy...

možná ještě přesněji -  v grafu se na ose y  se spíš odečítá pravá strana rovnice "tedy dráha jako funkce času",  zatímco na ose x se odečítá dejme tomu čas trvání jízdy...

v grafu by se měly všechny hodnoty z rovnice - tedy souhrnná, řídící či vnější neznámá "y" i "x", případně "z" a to i jejich mocniny s určitým zkreslením - respektive pod určitým úhlem promítat do osy "y" - zatímco osa "x" v grafu by měla figurovat jen jako časosběrná  osa - kde by zkoumané veličiny x,y případně z se měly podle průběhu daným rovnicí - tedy v grafu křivkou rozličně narůstat 

HRADLO ŽELEZNIČNÍ STANICE

"zahuštěný čas směny na hradle" - jakoby byla služba na hradle železniční stanice - kde osmihodinová směna jako by trvala například čtyřicet minut - funkci služby na hradle jakoby vycházela z kvadratické rovnice (tedy z rovnice s x na druhou) - kde je čas v exponentu ještě jednou - byť ve jmenovateli zlomku jako perioda - tímto způsobem se čas v kvadratické rovnici stává jako by zahuštěnější - než v běžné lineární rovnici - která odpovídá běžné vnímání času na nádražních hodinách - hodiny na hradle (pokud by se přistoupilo na příměr s kvadratickou rovnicí) by pak měly jakoby místo dvanácti - stočtyřicet čtyři hodin (dvanáct na druhou)  

JÍZDA

funkce v integrálním tvaru integráluzrychlení -  jakoby také umožňovala určit polohu vlaku - na podobném principu funguje navigace - nebo lineárním tvaru funkce prorychlost -  v obou případech je však klíčovou veličinou čas (přesněji perioda T) - a veličina "čas" je jak subjektem zrychlení - takrychlosti 

zrychlení

zrychlení je vlastně integrál ve vztahu k rychlosti - viz podrobnější informace a ilustrace např. zde v příspěvku

rychlost

(ovšem výpočty rychlosti se podrobněji zabývají jiné příspěvky - zejména příspěvek Mechanika KFD 1 DAV - frekvence, rychlost, zrychlení / proč rychlé vozy mají velká kola - Blog iDNES.cz a navazující příspěvky)

v = OMEGA xr (poloměr kola na druhou)

v = Mt (moment otáčení) x poloměr kola na prvou  

rychlost je vlastně lineární funkcí - která se přepočítává z tzv. úhlové rychlosti OMEGA na hřídeli přes moment otáčení (i když je možný i přímý přepočet z úhlové rychlosti - nicméně tento přepočet zahrnuje moment otáčení  

moment otáčení(momenty 1. stupně),  nebo rychlost rychlost, zrychlení (momenty 1. stupně) - započítává se jen kolo vozu (kolo 3)

vlastní funkce pro jízdu (na základě momentu otáčení Mt) – jedenkrát inverzní čas ve frekvenci (jmenovatel zlomku)

ROZJEZD
v kartézských souřadnicích těsně nad osou "x"
vlastní funkce "pro rozjezd (na základě momentu setrvačnosti Mi)"

moment setrvačnosti (moment 0. stupně) - vůz se zastavuje - odmocňuje se tou samou veličinou kterou se například počítá moment otáčení kola vozu během jízdy - zde se tedy z matematického hlediska uplatňuje odmocnina - variantně derivace

DERIVACE - PRŮNĚT JÍZDY 
hodnota rychlosti na ose "X"

 

 

výkonnostní osa Y 

- pokud se počítá kvadratická funkce  - křivka se zobrazuje poblíž osy Y

Integral či exponenciál funkce – dvakrát inverzní čas ve frekvenci (jmenovatel zlomku)

dvakrát inverzní čas ve frekvenci (jmenovatel zlomku) se vyskytuje rovněž pokud by se počítalo zrychlení - nebo například zjišťovala poloha vlaku ze dvou rychlostí danými jednou v souřadnicí y a podruhé x 

provozní meziosa XY - matematická funkce jedoucího vlaku podle které se zjišťuje rychlost 

vlastní funkce pro jízdu (na základě momentu otáčení Mt) – jedenkrát inverzní čas ve frekvenci (jmenovatel zlomku)

na displeji ve vlaku se zobrazuje okamžitá rychlost, z matematického hlediska pak spíš výsledek funkce - tedy cifra rychlosti - cifra, která se v kartézských souřadnicích by měla odečítat na ose y

různé vjemy z vlaku (například zvuk kol na kolejích) by však měly představovat spíš souhrn všech dílčích vjemů z jízdy vlakem, než jen samotný výsledek - možná přesněji předmět výpočtu - tedy rychlost

statistická osa X

DERIVACE - PRŮNĚT JÍZDY 
hodnota rychlosti na ose "y" - dráha, "x" - čas - tedy křivka jízdy se vlastně mění na polopřímku

případně - že se tato polopřímka zjišťuje derivací - nazývá se tato polopřímka "nárust funkce"

část 6
integrální a diferenciální počet z hlediska pozorovatele se zaměřením na rychlost 
veličina kterou vnímá služba na hradle je vlastně i n t e g r á l  r y c h l o s t i   
neboli r y c h l o s t  na  d r u h o u (veličina s dvakrát integrovaným časem)
nebo také r y c h l o s t  krát z m ě n a   r y c h l o s t

- jak se integrálů využívá pro zjištění polohy vlaku 

VÝKON
JÍZDA
ROZJEZD
DERIVACE - PRŮNĚT JÍZDY 
hodnota rychlosti na ose "X"

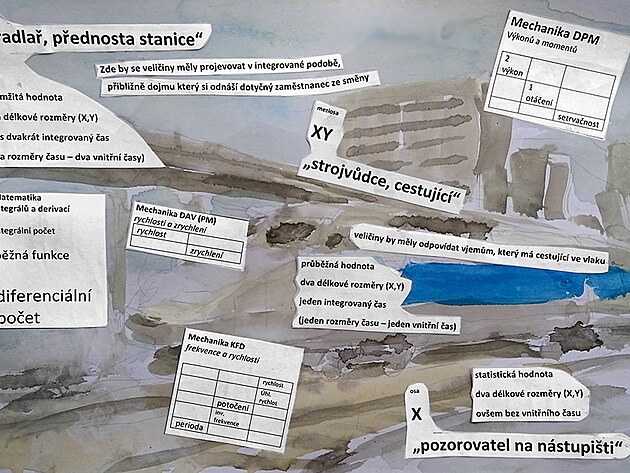
Přiřazení jednotlivých tématických okruhů v mechanice k různým jevům a úkonům které lze zjišťovat při jízdě vlaku či ve stanici.

Zkoumaná  veličina se jinak zobrazuje

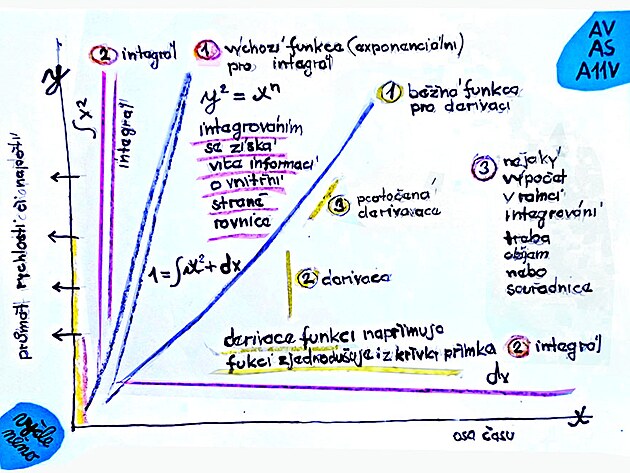
na výkonostní ose y - "hradlo, přednosta stanice"  kde se zobrazuje jako mocnina - nebo integrál - konkrétně například výkon jako bezčasová, okamžitá hodnota - z hlediska integrálních a diferenciálních počtů se vlastně jedná a veličinu s dvakrát integrovaným inverzním časem - nebo možná názorněji - tato veličina má dva rozměry délky - a dva podíly času - tedy se tato veličina jeví vlastně jako integrovaný obvod - řekněme zkomprimovaná do jednoho okamžiku - něco jako pocit který si odnáší služba na hradle ze směny - kdy se všechny děje zkomprimují do jednoho vjemu, či pocitu

na provozní meziose xy - "vlak, cestující ve vlaku, strojvůdce"  se zkoumaná veličina - například rychlost, eventuelně moment otáčení zobrazují cestujícímu ve vlaku ve zcela reálné, nezkreslené podobě - veličina zahrnuje dva délkové rozměry a jeden podíl  časem - tedy jeden integrovaný - nebo také vnitřní inverzní  čas frekvence -  ovšem z hlediska pozorovatele vně se vlastně jedná o integrál - a na příkladě integrálu lze vlastně názorně ozřejmit rozdíl mezi zrychlením a rychlostí .... zrychlení "a" je vlastně integrál bez "derivantu DELTA T"  - který má tu samou jednotku (vteřinu, minutu, hodinu) jako zrychlení a rychlost (a vlastně i tu samou jednotku jako perioda pohybu), a jelikož "derivant DELTA T" se vyskytuje pouze v rychlosti (nikoli ve zrychlení) - tak v rychlosti a zrychlení se jednotka času v čitateli a jmenovateli pokrátí  a z tohoto důvodu se tedy pouze ve zrychlení vyskytují například sekundy na druhou...

na statistické (časosběrné) ose x - "pozorovatel na nástupišti"  se zkoumaná veličina - například rychlost zobrazuje jako odmocnina - nebo derivace - určité rychlosti vlaku odpovídá například určitý interval času kdy vlak projíždí kolem pozorovatele na nástupišti -  zkoumaná veličina zahrnuje pouze teoreticky dva délkové rozměry (prakticky však jenom rozměr ve směru osy x., na ose veličina má nulovou hodnotu) - tato zkoumaná veličina nezahrnuje žádný rozměr času - tedy žádný vnitřní čas - přesto, že se na ose x odečítá právě hodnota času (ovšem veličina čas je zkoumána jako veličina x - tedy vlastně délka času)

délka jako vnímání rychlosti vně - "ubíhavost krajiny, rozmazanost vlaku" - derivace dráhy s (derivace již není funkcí času) - vlastně by se mělo jednat o inverzní jednotku délky - která se zkracuje s navyšující se rychlostí

(hradlo - vlak - nástupiště)
integrální a diferenciální počet z hlediska pozorovatele 

co  se vlastně počítá, jaký význam má levá a pravá strana v rovnici

Jaký je vlastně rozdíl mezi levou a pravou rovnice a rovnicí, funkcí a veličinou?

informační poznámka - obvyklý zápis rovnice je 

funkce  : Y (řídící neznámá) =X (výkonná neznámá)na entou

funkce  : Y =X na entou

dále v textu však poměrně často použito přehozené x a y 

tedy

funkce  : Y = X

veličina kterou nazírá pozorovatel na nástupišti při pohledu na jedoucí  je rychlost jako výsledek výpočtu (z matematického hlediska by mělo jít o levou stranu rovnice)

RYCHLOST  (jako funkce dráhy a času, vypočtená parciální  podílem nebo derivací), 

rychlost by měl vnímat pasažér ve vlaku sice také jako rychlost, ale z matematického hlediska spíš jde o funkce, pravá strana rovnice 

DRÁHA / ČAS

pozorovatel na nástupišti nazírá rychlost vlaku jako  výpočet funkce a to třeba podílem, nebo derivací   - to co vnímá pozorovatel vně vlastně jako rychlost se podobá vypočtené funkci, která vzhledem k faktu, že z rychlosti je vydělená veličina čas - tak rychlost vně se projevuje spíš jako délka - známá rozostřenost, či rozmazanost krajiny - vlastně není rychlost ale délka - onen rozmazaný vlak, který vnímá pozorovatel na nástupišti není nic jiného, než několik obrazců poskládaných za sebou (v kartézských souřadnicích pak ve směru osy X).

což je vyjádřeno slovy něco jako délka vlaku umocněná exponentem který se podle všeho navyšuje podle rychlosti vlaku čili něco jako "relativní délka vlaku" - tuto veličinu by bylo také možno nazvat "ubíhavost krajiny"

ve směru jízdy vlaku - tedy v kartézské soustavě v ose x je délková jednotka zastoupená vícekrát

dle této teorie 

by se pohybující vlak vlastně z hlediska pozorovatele na nástupišti vlastně nacházet 

ve quazi (či pseudo) vícerozměrném prostoru - kde je délková jednotka v ose x zastoupená vícekrát, podle toho, jak rychle vlak jede

při nazírání rozmazaného vlaku projíždějícím kolem nástupiště pozorovatel vlastně nenazírá rychlost ale derivaci rychlosti (řekněme ubíhavost krajiny) - a derivace má také jinou jednotku, kterou by teoreticky mohly být kilometry za hodinu na druhou (pokud se dělí rychlost časem) - jinak derivace rychlosti je bezčasová jednotka (navzdory časové jednotce v lomenině na druhou - což neznamená nic jiného že je tímto druhým dělením časem veličina čas z derivace - či podílu rychlosti jakoby vyloučena... 

INTEGRÁL RYCHLOSTI  (na hradle, či velíně)

rychlostí se dělí - nikoli násobí - je ve jmenovateli - jako freknce (lomeno časem)

rychlost "v" na druhou = dráha (jako funkce času) lomeno čas  

naopak integerál rychlosti je vlastně funkce dvou rychlostí a dvou časů,které v souřadnicích x,y můžou vymezit polohu vlaku

veličina která vznikne integrováním rychlosti by se možná dalo označit jako polohová rychlost - protože touto veličinou se vlastně určuje poloha vlaku - například

integrální a diferenciální počet se při pohybu (například vlaku) projevuje dvojím způsobem

integrální a diferenciální počet jako matematický zápis - z hlediska zobrazení do souřadnic 

část 7
integrální a diferenciální počet z hlediska pozorovatele 
veličina kterou vnímá služba na hradle je vlastně i n t e g r á l  r y c h l o s t i   
neboli r y c h l o s t  na  d r u h o u (veličina s dvakrát integrovaným časem)
nebo také r y c h l o s t  krát z m ě n a   r y c h l o s t i 

výkonnostní osa Y - z hlediska dispečera na hradle

jinak vnímá děje výpravčí na hradle (jako integrál s dvakrát integrovaným časem)  - tedy jakoby se výpravčímu všechny děje za směnu integrovaly do jednoho pocitu který si odnáší ze směny - a zjišťovaný děj (třeba rychlost konkrétního vlaku který toho dne projel nádražím) musí dejme tomu vybalit z paměti...

veličina kterou vnímá služba na hradle je vlastně i n t e g r á l  r y c h l o s t i   

neboli r y c h l o s t  na  d r u h o u (veličina s dvakrát integrovaným časem)

nebo také r y c h l o s t  krát z m ě n a   r y c h l o s t i 

kterou se udává třeba  poloha vlaku

provozní meziosa XY

zde rychlostzobrazovaná jakofunkce (nikoli jako výsledek čí prostředek výpočtu, tedy konkrétní číslo

jinak děje vnímá cestující ve vlaku - a to jako  matematickou funkci - nyní je záleží z jakého vzorce se rychlost vlastně počítá

dráha podle času ku časovému intervalu jako rychlost

a jinak se zobrazuje pozorovateli vně

a název pro veličinu popisující  rozmazaný vlak vnímaný pozorovatelem z nástupiště by mohl znít

délka jako vnímání rychlosti vně - "ubíhavost krajiny, rozmazanost vlaku" - derivace dráhy s (derivace již není funkcí času) - vlastně by se mělo jednat o inverzní jednotku délky - která se zkracuje s navyšující se rychlostí

zda 

TŘI METODY VÝPOČTU RYCHLOSTI

1/ dráha lomeno čas,

2/ z pohybu rovnoměrného či zrychleného  (zde s jednou integrovaným časem) - takže se vlastně jedná o něco jako integrál, nebo alespoň pseudointegrál (kde jednu složku - užší funkci tvoří zrychlení (při rovnoměrném pohybu rovno jedné) a druhou složku vlastní rychlost - která se počítá jako obvodový úhel kružnice (obsažený ovšem ve zrychlení) kterým se násobí časový rozdíl od rozjezdu po okamžik - kdy se zjišťuje rychlost

mimochodem - z tohoto pojetí - tedy z jedoucího vlaku - přesně z frekvence pohonu - vychází vlastní vzorec pro výpočet rychlosti (zde v příspěvku v části 2 - případně v jiných příspěvcích) - tedy vzorec pro výpočet rychlosti na základě frekvence pohonu - takže lze rozlišit zda se jedná o pohyb rovnoměrný nebo zrychlený, na rozdíl od standartního výpočtu rychlosti dráha/čas - který je zmíněn následně

3/ nu a třetím způsobem, jak možno spočítat rychlost je z frekvence (periody) pohonu

konkrétněji například v příspěvku Mechanika KFD / DAV - frekvence, rychlost, zrychlení / proč rychlé vozy mají velká kola - Blog iDNES.cz

(METODA RYCHLOST JAKO DVOSLOŽKOVÁ VELIČINA - TEDY POHYB ROVNOMĚRNÝ (rychlost v užším smyslu) krát  POHYB ZRYCHLENÝ naznačena zde v závěru příspěvku, v části 4

přímý výpočet rychlosti jako funkcezrychlení (které představuje něco jako hlavní funkci integrálu) a časosběrného intervalu (který představuje něco jako derivant integrálu)

statistická osa X

a konečně jinak děje vnímá pozorovatel na nástupišti - kterému se vlastně zobrazuje nikoli rychlost - ale derivace rychlosti  (bez komprimovaného času) - což je něco jako "rozmazaná délka vlaku" - kde jako koeficient rozmazanosti možno považovat exponent derivace

OBSAH

rozcestník matematika 

část 1 
rozdíl mezi rovnicí a funkcí - průběh funkce

část 2 
přepočty výkon - rychlost - rozjezd 

část 3
rozdíl mezi x a y v kartézských souřadnicích, a rozdíl mezi x a y v rovnici (tedy ve funkci) hradlo - vlak - nástupiště

část 4
integrální a diferenciální počet - obecné pojednání
diferenciální počet
integrální počet

část 5
poloha vlaku v souřadnicích, rychlost vlaku a "ubíhavost" krajiny"
co  se vlastně počítá, jaký význam má levá a pravá strana v rovnici

část 6 
integrální a diferenciální počet z hlediska pozorovatele
integrální a diferenciální počet jako matematický zápis - z hlediska zobrazení do souřadnic
 integrální a diferenciální počet jako matematický zápis - z hlediska zobrazení do souřadnic
VÝKONhradlo - vlak - nástupiště
JÍZDA
ROZJEZD
DERIVACE - PRŮNĚT JÍZDY 
hodnota rychlosti na ose "X"

část 7
integrální a diferenciální počet z hlediska pozorovatele 
veličina kterou vnímá služba na hradle je vlastně i n t e g r á l  r y c h l o s t i   
neboli r y c h l o s t  na  d r u h o u (veličina s dvakrát integrovaným časem)
nebo také r y c h l o s t  krát z m ě n a   r y c h l o s t i 

část 8
tři metody výpočtu rychlosti 
výpočet rychlostí jako dvousložkové veličiny (zrychlený pohyb krát rovnoměrný pohyb), výpočet rychlosti dráha lomeno čas) 
rychlost nebo zrychlení (matematika DAV)

část 8
tři metody výpočtu rychlosti 
výpočet rychlostí jako dvousložkové veličiny (zrychlený pohyb krát rovnoměrný pohyb), výpočet rychlosti dráha lomeno čas) 
rychlost nebo zrychlení (matematika DAV)

 

opakování - zde by vlastně měly být porovnány, či představeny dvě metody výpočtu rychlosti (jednak metoda vycházející přímo z funkce rychlosti jedoucího vlaku - na základě frekvence pohonu a druhá metoda vycházejícího ze standartního výpočtu rychlosti dráha lomeno čas

provozní meziosa XY

(výpočet rychlosti na základě frekvence pohonu)

jinak děje vnímá cestující ve vlaku - jako formálně jako běžnou matematickou funkci (s jednou integrovaným časem) - takže se vlastně jedná o něco jako integrál, nebo alespoň pseudointegrál (kde jednu složku - vlastní funkci tvoří zrychlení (při rovnoměrném pohybu rovno jedné) a druhou složku vlastní rychlost - která se počítá jako obvodový úhel kružnice (obsažený ovšem ve zrychlení) kterým se násobí časový rozdíl od rozjezdu po okamžik - kdy se zjišťuje rychlost

- mimochodem - z tohoto pojetí - tedy z jedoucího vlaku - přesně z frekvence pohonu - vychází vlastní vzorec pro výpočet rychlosti (zde v příspěvku v části 2 - případně v jiných příspěvcích) - tedy vzorec pro výpočet rychlosti na základě frekvence pohonu - takže lze rozlišit zda se jedná o pohyb rovnoměrný nebo zrychlený, na rozdíl od standartního výpočtu rychlosti dráha/čas - který je zmíněn následně 

z hlediska cestujícího ve vlaku - tedy jako přímého účastníka je zobrazení jednotlivých veličin v kartézských souřadnicích následující...

na výkonnostní ose Y se cestujícímu ve vlaku zobrazuje dráha "s"

na provozní meziose XY se zobrazuje rychlost (v podstatě subjektem této veličiny je i přímo cestující) - zpravidla ve tvaru nějaké křivky (podle toho, zda se jedná o pohyb rovnoměrný, či zrychlený (ovšem při výpočtech v kartézských souřadnicích se vlastně přímo přepočítává veličina zobrazovaná na osu X (v tomto případě dráha "s") - vlastní funkce se zobrazuje, jak bylo zmíněno kolem provozní meziosy - takže počítat rychlost jako funkci podobající se integrálu jako křivky není sice obvyklé - nicméně tento přímý výpočet je zde představen 

na statistické ose X se cestujícímu zobrazuje čas - čas jako časosběrná veličina se ovšem zobrazuje i při dalších variantách zkoumání pohybu - a to z vnějšího hlediska "pomyslného dispečera na hradle - kterému se na ose Y zobrazují veličiny pohybu v integrované podobě - dále na ose Y z vnitřního hlediska v integrované podobě - kdy se zobrazuje výkon - rovněž v derivované podobě s vnitřního i vnějšího hlediska se v obou případech na výkonnostní ose Yzobrazuje rychlost- přičemž na statistické ose X se úplně ve všech zde uvedených případech tyto veličiny porovnávají se veličinou čas 

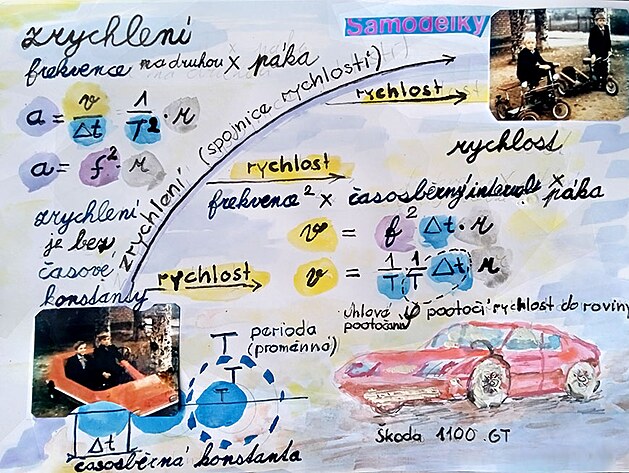
vzorec pro výpočet rychlosti na základě frekvence pohonu (neboli rychlost jako integrál)

rychlost = zrychlení (které zahrnuje i úhlovou dráhu) x časosběrný interval DELTA T (čas od rozjezdu do zkoumané hodnoty času) 

přičemž rychlost  při rovnoměrném (nezrychleném) pohybu je hodnota zrychlení rovna jedné - a velikost rychlosti vlastně odpovídá jedna ( jako úhlová dráha při jedné otáčce)  k r á t časosběrný interval DELTA T (čas od rozjezdu do zkoumané hodnoty času) 

statistická osa X

(výpočet rychlosti statistickou metodou - tedy dráha lomeno čas)

a konečně jinak děje vnímá pozorovatel na nástupišti - kterému se vlastně zobrazuje čistá rychlost vlaku (bez komprimovaného času) - ovšem  veličiny potřebné pro výpočet rychlosti standartním výpočtem rychlosti (podle statistického vzorce dráha lomeno čas) lze zjistit měřením nebo odhadem - a to jednak délky nástupiště - a jednak zjištěním doby průjezdu vlaku například z nádražních hodin

jiná metoda výpočtu rychlosti

výpočet rychlosti statistickou metodou zrychlený pohyb krát rovnoměrný pohyb - neboli metodou zrychlení krát derivant času

TATO METODA VÝPOČTU RYCHLOSTI NENÍ JEŠTĚ ZCELA OVĚŘENA, NICMÉNĚ ZRYCHLENÍ BY SE MĚLO VYNÁSOBIT ČASEM DRÁHY v tomto spočívá princip výpočtu ...

další metoda zjišťování rychlosti - jak měří rychlost policie

Standartní metodu zjišťování rychlosti  požívá, či používala například policie (dříve VB) - která měřila měřila rychlost projíždějících vozidel na vymezeném úseku na základě času z bodu A do bodu B

dříve zjištěním času na stopkách hodin

později radarem 

nicméně tento definiční vzorec pro rychlost, statistický výpočet rychlosti je vlastně z hlediska integrálních a diferenciálních počtů nepřímým výpočtem rychlosti - vlastně derivací rychlosti 

 

k tématu zrychlení rovněž doplněna pasáž z cyklu příspěvků "DAV" - rychlost a zrychlení 

4DAV/ dynamika rychlosti a zrychlení

veličina zrychlení a veličina výkon zahrnují frekvenci (neboli inverzní čas vlastně dvakrát)

veličina zrychlení se vlastně zdánlivě podobá veličině výkon (ovšem zrychlení pozorovatel vně reálně vnímá, zatímco výkon nikoli, výkon jakoby se odehrával v čase na mínus druhou - tedy něco jako 144 hodinovém dni) - dvakrát frekvence a poloměr kola, ze zrychlení nelze zjistit dráha - zrychlení by bylo možno označit jako funkci průběhu rychlosti

rychlost je frekvence (například kola vozu) násobená úhlovým potočením kola a poloměrem kola - lze tedy přepočítat na dráhu - ovšem zrychlení na rozdíl od rychlosti prvek dráhy neobsahuje

Zrychlení je změna rychlosti (někdy taky označované jako  změna změny - ale je otázka nakolik je toto označení výstižné), na rozdíl od rychlosti zrychlení chybí prvek dráhy .

Průměrné zrychlení  objektu za určitou dobu je jeho změna rychlosti. 

MOŽNÁ BY PRO ZRYCHLENÍ NEŽ ZMĚNA ZMĚNY BYL VÝSTIŽNĚJŠÍ POJEM "NEÚPLNÝ VÝKON"

Z hlediska matematiky se jedná o podíl k rychlosti, nebo dvojí podíl času k dráze.

Okamžité zrychlení 
je limitem průměrného zrychlení v nekonečně malém časovém intervalu. 
 

Z hlediska integrálních a diferenciálních počtů je okamžité zrychlení derivací vektoru rychlosti vzhledem k času, v nekonečně malém časovém intervalu.
Z hlediska integrálních a diferenciálních počtů  jde o deravici druhého řádu k dráze. v nekonečně malém časovém intervalu.

rychlost přepočtem z frekvence otáčení kola (na podobném principu pravděpodobně funguje i tachometr)

rozjezd (moment setrvačnosti - zde označen jako moment nultého stupně  bez času, podobný momentům ve statice) - jízda (moment otáčení, rychlost, zrychlení - značené jako momenty 1. stupně)  až po zjištění výkonu (zde označen jako moment 2. stupně

Nádraží a vlak - rychlost a zrychlení - mechanika integrálních a diferenciálních počtů  AV

OBSAH na závěr

rozcestník matematika 

část 1 
rozdíl mezi rovnicí a funkcí - průběh funkce

část 2 
přepočty výkon - rychlost - rozjezd 

část 3
rozdíl mezi x a y v kartézských souřadnicích, a rozdíl mezi x a y v rovnici (tedy ve funkci) hradlo - vlak - nástupiště

část 4
integrální a diferenciální počet - obecné pojednání
diferenciální počet
integrální počet

část 5
poloha vlaku v souřadnicích, rychlost vlaku a "ubíhavost" krajiny"
co  se vlastně počítá, jaký význam má levá a pravá strana v rovnici

část 6 
integrální a diferenciální počet z hlediska pozorovatele
integrální a diferenciální počet jako matematický zápis - z hlediska zobrazení do souřadnic
 integrální a diferenciální počet jako matematický zápis - z hlediska zobrazení do souřadnic
VÝKONhradlo - vlak - nástupiště
JÍZDA
ROZJEZD
DERIVACE - PRŮNĚT JÍZDY 
hodnota rychlosti na ose "X"

část 7
integrální a diferenciální počet z hlediska pozorovatele 
veličina kterou vnímá služba na hradle je vlastně i n t e g r á l  r y c h l o s t i   
neboli r y c h l o s t  na  d r u h o u (veličina s dvakrát integrovaným časem)
nebo také r y c h l o s t  krát z m ě n a   r y c h l o s t i 

část 8
tři metody výpočtu rychlosti 
výpočet rychlostí jako dvousložkové veličiny (zrychlený pohyb krát rovnoměrný pohyb), výpočet rychlosti dráha lomeno čas) 
rychlost nebo zrychlení (matematika DAV)