- Napište nám
- Kontakty
- Reklama
- VOP
- Osobní údaje
- Nastavení soukromí
- Cookies
- AV služby
- Kariéra
- Předplatné MF DNES
Mechanika KFD 1 DAV - frekvence, rychlost, zrychlení / proč rychlé vozy mají velká kola
OBSAH
ukázka podstatných částí příspěvku
rozcestník auto Škoda
rozcestník kinematika
1KFD/ kinematika - frekvence, perioda, úhlová dráha (fotbalového míče)
rozcestník frekvence, perioda, amplituda - mechanika i elektrotechnika
2 KFD/ kinematika - frekvence, perioda, úhlová dráha, úhlová rychlost (přechodová veličina mezi kinematikou a dynamikou)
proč rychlé vozy mají velká kola
motocykly se závěsným motorem
odkaz na rozcestník výkon
2.3 KDF/DPM rozcestník pro přepočty "kinematika - dynamika - MECHANICKÉ KOLO"
3DPM/ dynamika výkonů a momentů a výsledné rychlosti
4DAV/ dynamika rychlosti a zrychlení - pohyb rovnoměrný, rovnoměrně a nerovnoměrně zrychlený
rozcestník "rychlost a zrychlení"- pohyb rovnoměrný, rovnoměrně a nerovnoměrně zrychlený
5/ příběh automobilky Laurin a Klement - Škoda auto
6/ velká kola - velká rychlost - nebo malá spotřeba
7/ autonomní vozidla
Ukázka podstatných částí příspěvku
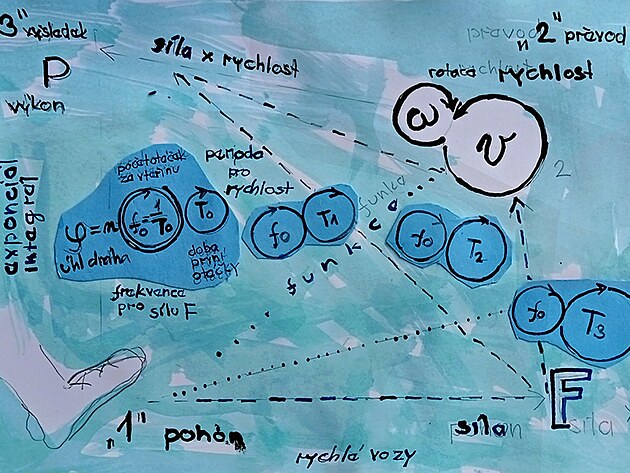
Základními veličinami v mechanice pohybu je síla F a rychlost v - přičemž jako by spíš platilo buď síla - nebo buď rychlost - než síla a rychlost. Obě veličiny lze vzájemně přepočítat. Určitou souhrnnou veličinou - která do jisté míry zahrnuje obě veličiny - tedy rychlost i sílu je pak výkon - ovšem veličinu výkon P zkoumají spíše jiné příspěvky zde označené jako mechanika DPM. Pohyb lze tedy vyjádřit sílou i rychlostí - přičemž z hlediska přiřazení dalších veličin - popisující mechanický pohyb je pravděpodobně názornější vyjadřovat pohyb prostřednictvím veličiny rychlost. Ostatně sílu a rychlost lze vzájemně přepočítat - čímž se zabývá například příspěvek Matematická mechanika A0/ KFD 0 jak měří siloměr přes rychlost sílu / výpočty přes stopky - Blog iDNES.cz .
Proč je rychlost výhodnější nebo názornější než síla?
Rychlost zahrnuje několik dílčích veličin - které podobně jako výsledná rychlost definují pohyb ( a to zejména veličiny frekvence a perioda + dále rychlost zahrnuje další dílčí veličiny - a to zejména veličinu úhlová dráha PSÍ - která by zase jakoby do rychlosti zahrnovala i hmotnost automobilu - případně i hmotnost přepravovaného břemene... Pokud při fotbalovém utkání kopne do dvou míčů se stejnou silou - a jeden míč se kotálí déle - či rychleji naznačuje, že tento míč má menší váhu - čili hmotnost - liší se tedy nejen výsledná dráha míče - ale i tzv. úhlová dráha PSÍ - ze které lze přepočítat standartní dráhu.
Kromě dílčích složek - což jsou v případě rychlosti frekvence, perioda - tzv. úhlová rychlost OMEGA na ose hřídele - k veličině rychlost jako by náležely i další - odvozené veličiny - podle kterých se pohyb rozlišuje na pohyb rovnoměrný, rovnoměrně zrychlený - nebo pohyb nerovnoměrně zrychlený.
Odvozeno veličinou od veličiny rychlost "v" je zejména zrychlení "a" - zrychlením by se měl rovněž zabývat tento příspěvek...
Přepočet „obojí rychlosti“ vozu jako celku a dráze o zkoumaném intervalu času (době jízdy) delta t a rychlosti otáčení kola o čase (periodě) T
OBSAH
ukázka podstatných částí příspěvku
rozcestník auto Škoda
rozcestník kinematika
1KFD/ kinematika - frekvence, perioda, úhlová dráha (fotbalového míče)
rozcestník frekvence, perioda, amplituda - mechanika i elektrotechnika
2 KFD/ kinematika - frekvence, perioda, úhlová dráha, úhlová rychlost (přechodová veličina mezi kinematikou a dynamikou)
proč rychlé vozy mají velká kola
motocykly se závěsným motorem
odkaz na rozcestník výkon
2.3 KDF/DPM rozcestník pro přepočty "kinematika - dynamika - MECHANICKÉ KOLO"
3DPM/ dynamika výkonů a momentů a výsledné rychlosti
4DAV/ dynamika rychlosti a zrychlení - pohyb rovnoměrný, rovnoměrně a nerovnoměrně zrychlený
rozcestník "rychlost a zrychlení"- pohyb rovnoměrný, rovnoměrně a nerovnoměrně zrychlený
5/ příběh automobilky Laurin a Klement - Škoda auto
6/ velká kola - velká rychlost - nebo malá spotřeba
7/ autonomní vozidla
Otázka zní - dva hráči kopnou do dvou míčů - nebo udeří do koule kulečníku - na začátku se míče kotálí se stejnou frekvencí - jeden se však rychleji zpomalí - a druhý dokotálí dál ... proč to?
Pohyb jakoby by bylo možno rozčlenit do dvou složek - rovnoměrný pohyb krát zrychlený (variantně zpomalený pohyb). Například při jízdě vozu je rovnoměrnou složkou pohybu vozu průměrná, či běžná cestovní rychlost - a zrychlená, či zpomalená složka pohybu se přidá k rovnoměrnému pohybu zejména při rozjezdu či dojezdu - čímž se vytvoří výsledný zrychlený (či zpomalený) pohyb - pokud by se pohyb vozu analyzoval.
Do určité míry kopíruje i toto rozdělení pohybu i veličina rychlost - pokud se počítá s frekvence otáčení kola.
Za univerzální vzorec pro veličinu rychlost "v" - pokud se rychlost zjišťuje přímo z pohybu - lze považovat součin rychlost = frekvence krát úhlová dráha krát poloměr (kola)...
Přičemž za rovnoměrnou (či fixní složku rychlosti) lze považovat jednak poloměr kola "r" a jednak počáteční - případně průměrnou periodu To, která je ovšem jednou ze složek veličiny úhlová dráha "psí" - tou druhou složkou úhlové dráhy je opět frekvence (úhlová dráha vlastně vznikne když se porovnává počáteční perioda To s frekvencí - přesněji s okamžitou frekvencí f).
Za proměnnou (zrychlenou, zpomalenou) složku rychlosti lze považovat frekvenci f.
Za rovnoměrnou, či fixní složku pohybu lze v případě fotbalové míče lze považovat počáteční rychlost - pokud by se takto analyzovala samotná veličina rychlost - za rovnoměrnou složku pohybu by bylo možno považovat dobu jedné otáčky - tedy periodu fotbalového míče značenou jak periodaTo.
Mechanika KFD / DAV - frekvence, rychlost, zrychlení / kinematika fotbalového míče / proč rychlé vozy mají velká kola
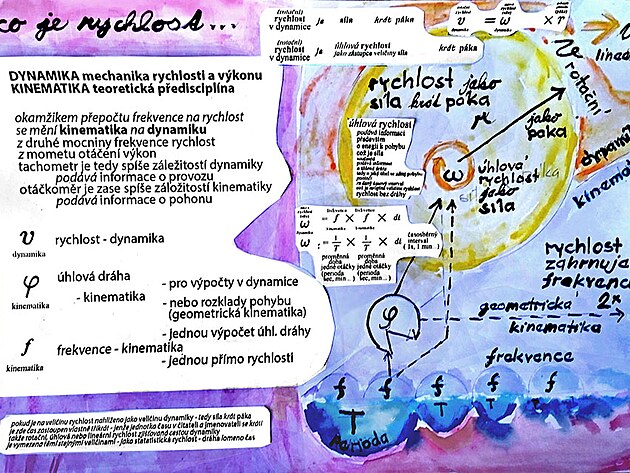
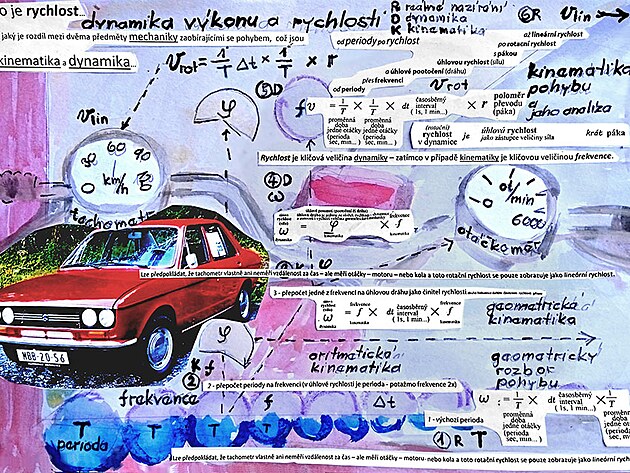
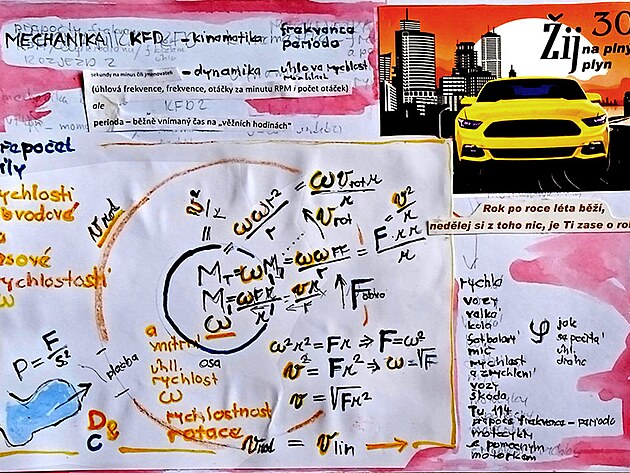
Čím se liší frekvence, rychlost, zrychlení a proč rychlé vozy mají velká kola - a také v jakém okamžiku se mění disciplína mechaniky kinematika na druhou disciplínu mechaniky pohybů - tedy dynamiku - otázka na jejíž zodpovězení by mohl přispět tento příspěvek.
kinematická frekvence - je velmi nenázorná veličina - stejná frekvence je v ose pohonu, stejný frekvence je na obvodu převodu - a navíc je vyjádřena v inverzních sekundách na mínus prvou - a dále se jedná o čistě teoretickou veličinu - sondu v ose kola
OBSAH
ukázka podstatných částí příspěvku
rozcestník auto Škoda
rozcestník kinematika
1KFD/ kinematika - frekvence, perioda, úhlová dráha (fotbalového míče)
rozcestník frekvence, perioda, amplituda - mechanika i elektrotechnika
2 KFD/ kinematika - frekvence, perioda, úhlová dráha, úhlová rychlost (přechodová veličina mezi kinematikou a dynamikou)
proč rychlé vozy mají velká kola
motocykly se závěsným motorem
odkaz na rozcestník výkon
2.3 KDF/DPM rozcestník pro přepočty "kinematika - dynamika - MECHANICKÉ KOLO"
3DPM/ dynamika výkonů a momentů a výsledné rychlosti
4DAV/ dynamika rychlosti a zrychlení - pohyb rovnoměrný, rovnoměrně a nerovnoměrně zrychlený
rozcestník "rychlost a zrychlení"- pohyb rovnoměrný, rovnoměrně a nerovnoměrně zrychlený
5/ příběh automobilky Laurin a Klement - Škoda auto
6/ velká kola - velká rychlost - nebo malá spotřeba
7/ autonomní vozidla
rozcestník auto Škoda
"úvodní příspěvek" Mechanika A/ KFD : kinematika (frekvence), dynamika (úhlová a obvodová rychlost - Škoda - Blog iDNES.cz a současně rozcestník pro doplňkové výpočty v matematice a mechanice - úhlové míry, přepočty druhů frekvence
"osobní automobily" Mechanika KFD / DAV - frekvence, rychlost, zrychlení / proč rychlé vozy mají velká kola - Blog iDNES.cz (tento příspěvek)
"nákladní automobily Mechanika DPM 2 /W moment setrvačnosti / úhlová rychlost - moment síly - síla / výkon okamžitý z frekvence a statistický z práce - nákladní vozy 2 - Blog iDNES.cz(album na závěr příspěvku)
rozcestník matematika
vnitřní matematika – matematika přepočtů
vnější matematika – matematické funkce (i pro jiné obory)
rozcestník kinematika
Mechanika KFD - linie frekvence - perioda - úhlová dráha (potočení) - úhlová rychlost na ose
KFD 0
rozcestník pro matematiku a mechaniku pohybu Mechanika A0/ KFD 0 rozcestník matematická mechanika a jak měří siloměr přes rychlost sílu, úhlová rychlost jako potenciál pohybu - Blog iDNES.cz příspěvek srovnává především dva zdroje pohybu - statickou sílu na obvodu kola - ze které plyne moment síly (z něhož částečně vyplývá i soustružnický efekt) a kinematickou sílu na ose hřídele- ze které zase vyplývá rychlost - výpočet momentu otáčení - případně přepočet momentu otáčení z rychlosti
KFD 1
doplňkové výpočty
různé druhy frekvence a radián, úlové míry a obvod Mechanika DPM 2 /W moment setrvačnosti / úhlová rychlost - moment síly - síla / výkon okamžitý z frekvence a statistický z práce - nákladní vozy Škoda, Liaz a Praga - Blog iDNES.cz (tento příspěvek) a stejně zaměřený příspěvek Mechanika A/ KFD - Ludolfovo číslo a radián doplňkové výpočty v kinematice, bývalá opravna Škoda Jihlava - Blog iDNES.cz
přepočty různých druhů frekvence a úhlová dráha zkoumány v příspěvku Mechanika A3/KFD3 - radián, druhy frekvence, rychlé vozy (sanitky) a jejich rozjezd 1 - Blog iDNES.cz
rozcestník pro kinematiku
úvodní příspěvek -"osobní automobily Škoda" Mechanika KFD / DAV - frekvence, rychlost, zrychlení / kinematika fotbalového míče / proč rychlé vozy mají velká kola - Blog iDNES.cz (tento příspěvek) - podrobně zpracovaná zejména matematická linie přepočtů)
KFD 2
Cyklistika 2 Mechanika C2/KFD 2 - pomaluběžný nebo rychloběžný motor, cyklistické a motoristické pohony a také závody - Blog iDNES.cz - podrobně zpracovaná zejména matematická linie přepočtů jako v příspěvku 1 "rychlé vozy"
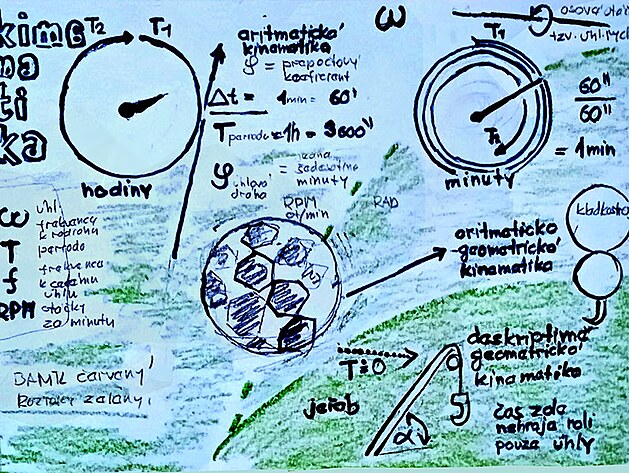
aritmetická kinematika (s inverzním časem ve frekvenci)
aritmeticko - geometrická kiematika (frekvence přepočtená na úlovou dráhu)například u převodů
deskriptivně - geometrická kinematika (například u stavebních strojů) kde mají význam zejména úhly mezi jednotlivými členy mechanismu
Dálniční most přes Křešické údolí 3 - kinematika stavebních strojů a stavba mostů - Blog iDNES.cz
Mechanika KFD 4
návštěva tiskárny a části strojů - Návštěva staré tiskárny - části strojů a mechanismy - Blog iDNES.cz - tři způsoby grafického zobrazování pohybu: podle dráhy a trajektorií / podle obálky / podle polodií
Mechanika KFD L
přepočty frekvence - rychlost v letectví Letoun Avia Av-57, jak se počítá na tachometru rychlost letounu 4 - Blog iDNES.cz
prostorová rychlost letecké vrtule (jedna složky na obvodu a druhá složka ve směru letu) Mechanika DHM - hybnost, moment hybnosti, změna hybnosti a letouny Iljušin v Brně Slatině - Blog iDNES.cz
rozcestník zrychlení (mechanika DAV)
Mechanika KFD 1 DAV - frekvence, rychlost, zrychlení / proč rychlé vozy mají velká kola (tento příspěvek)
Mechanika DAV(PM): Holešov - pohyb rovnoměrný, rovnoměrně a nerovnoměrně zrychlený Z 142 - Blog iDNES.cz letiště Holešov
úhlové zrychlení je definováni jako derivace úhlové dráhy podle času C2 Mechanika KFD 2 - pomalu a rychlo - běžný motor, cyklistické závody, druhy motopohonů - Blog iDNES.czz
rozcestník dynamika
DPM 1
Mechanika DPM1 - Výkon, nebo točivý moment - proč má traktor velké zadní kolo a je pomalý? - Blog iDNES.cz se zaměřením na přepočty síla - moment síly - rychlost
DPM 2
se zaměřením na přepočty veličin síla - práce - moment síly - výkon Mechanika DPM 2 /W moment setrvačnosti /úhlová rychlost - moment síly - síla / výkon okamžitý z frekvence a statistický z práce - nákladní vozy 2 - Blog iDNES.cz
výkon v letectví Letecký tachometr a tah, rychlost a výkon proudového letounu , letiště Žatec a Mig 29 - Blog iDNES.cz
1KFD/ kinematika - frekvence, perioda, úhlová dráha (fotbalového míče)
,
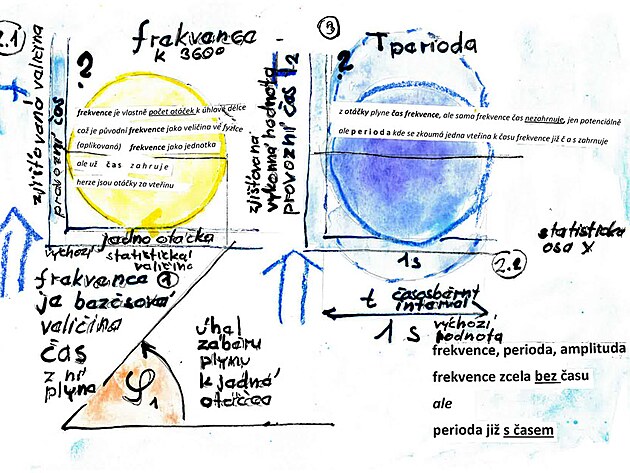
frekvence f
otáčky za vteřinu
(frekvencí je i úhlová rychlost omega, úhlová frekvence omega a otáčky za minutu RPM - liší de buď úhlem - radián, proměnlivý úhel, celý obvodový úhel´- nebo intervalem)
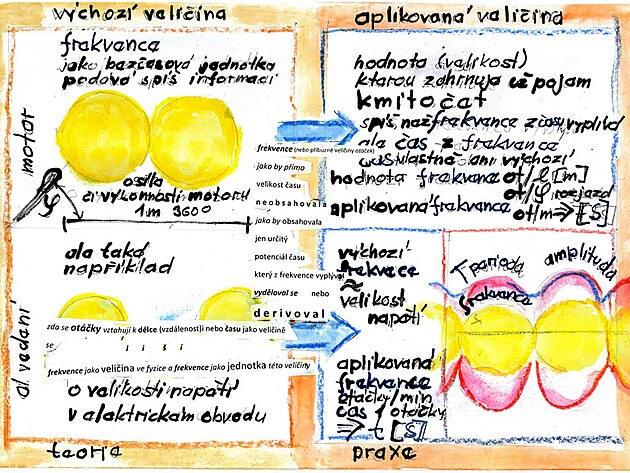
perioda T
doba otáčky (při referenční intervalu frekvence - což je jedna vteřina) - tedy čas jako provozní veličina (inverze frekvence) - a podle této veličiny by se měla měnit výška elipsy periody
PERIODA VLASTNĚ ZAHOJU DVĚ FORMY ČASU
VÝKONNÝ ČAS
na výkonové ose y - čas jedné otáčky - velikost tohoto času je proměnlivá
STATISTICKÝ ČAS
na statistické ose x- časosběrný interval frekvence - tedy jedna vteřina
jinými slovy - průběh periody má tvar ELIPSY - kde je stálý rozměr na ose x
amplituda
něco jako spojnice periody - přizpůsobená tvaru periody
jako výchozí veličina pro výkop fotbalového míče - lze označit veličinu podobající se hmotnosti míče - ale lišící se od hmotnosti hlavně tím - že jde o matematickou funkci
impuls síly je tedy veličina v jakémsi bezčasí - při ose x (zdrojová položka pro vyvinutí síly výkopu)
Newton·sekunda [N·s]. je rovněž jednotkou jiné mechanické veličiny - kterou je impuls síly. Impuls síly jako bezčasová veličina ovšem lze například nahradit momentem setrvačnosti - který je také bezčasový a dá se přepočítat přes moment setrvačnosti a momentovou větou na základě rovnosti dvojic momentů páka - záběr o čemž například pojednává příspěvekMechanika A3/KFD - radián, frekvence, rozjezd a výkon sanitky, rozcestník Avia - Blog iDNES.cz.
De facto se impuls síly rovná změně hybnosti, kterou by by bylo možno možná názorněji označit jako "sílu s vyděleným časem"- čímž vzniká veličina podobající se hmotnosti (jakožto výchozí položka pro pohyb, na rozdíl od hmotnost je impuls síly matematickou funkcí...
Také se používá impuls síly - změna hybnosti , ale změnou hybnosti se vlastně klasifikuje a kvantifikuje výchozí zátěž kterou bude potřeba překonat.
Z hlediska zařazení do širší skupiny fyzikálních veličin patří impuls síly k rozběhovým momentům 0téeho řádu.
podrobněji k veličinám moment hybnosti, hybnost a impuls síly v příspěvku Mechanika DHM - hybnost, moment hybnosti, změna hybnosti a letouny Iljušin v Brně Slatině - Blog iDNES.cz
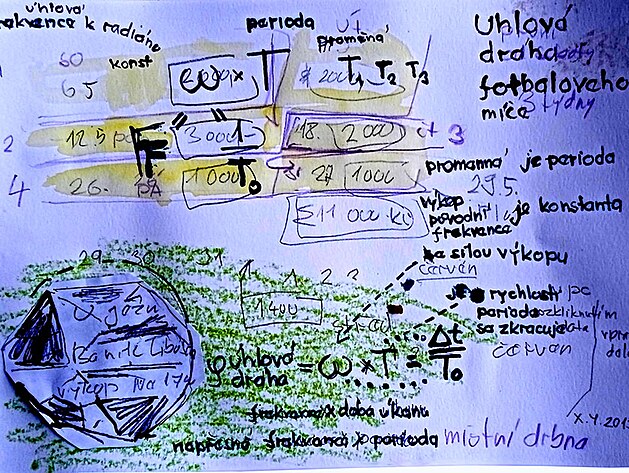
úhlová dráha je poměrně důležitá veličina pro přepočet konstantní frekvence ze síly (výkop míče) a rychlosti se zkracující se periody (míč po výkopu, kotálející se míč) - jednak na dráhu míče - a jednak na další veličiny v kinematice a dynamice
Otázka zní - dva hráči kopnou do dvou míčů - nebo udeří do koule kulečníku - na začátku se míče kotálí se stejnou frekvencí - jeden se však rychleji zpomalí - a druhý dokotálí dál ... proč to?
pokus o odpověď
Pravděpodobnou příčinou je veličina úhlová dráha (frekvence i perioda - tedy čas To je stejné - ale úhlová dráha zahrnuje ještě jednu veličinu čas - a to DELTA T - což je vlastně doba kotálení míče - v úlové dráze se čas v čitateli a jmenovateli pokrátí a pak se ještě násobí poloměrem - nicméně rozdíl v poměru mezi celkovým časem a časem první otáčky se projeví právě ve velikosti úhlové dráhy "psí" - a tato veličina - úhlová dráha by byla možná být označena i jako potenciál pohybu - čím větší je tedy doba pohybu DELTA T - tím větší i úhlová dráha "psí" - a tím větší je i úhlová rychlost OMEGA!
jeden míč urazí dejme tomu dráhu 20 metrů a časem DELTA T1
druhý míč dráhu 50 metrů s odlišným časem DELTA T2
A proč tento rozdíl - když počáteční rychlost je stejná - pravděpodobnou příčinou je rozdíl v hmotnosti jednoho a druhého míče - i když hmotnost není vůbec ve výpočtech zahrnuta... nebo koule kulečníku – viz obrázek výše
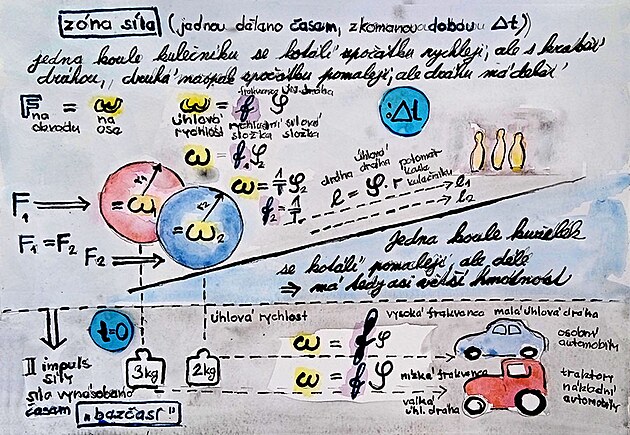
nebo příklad s koulemi kulečníku – hráč udeří stejnou sílou F nejprve například do modré koule – podruhé například do červené koule – jedna koule se začne kotálet rychleji, ale rychle se zpomalí a má kratší dráhu, druhá koule je na začátku pomalejší – ale má dráhu delší ...
síla F působící na obvodu má stejný účinek jako úhlová rychlost OMEGA na ose hřídele
červená koule kulečníku: úhlová rychlost OMEGA = nižší frekvence x větší úhlová dráha
modrá koule kulečníku: tatáž úhlová rychlost OMEGA na hřídeli = vyšší frekvence x kratší úhlová dráha
proč tento rozdíl? – jedna koule musí mít větší hmotnost (červená) a druhá menší hmotnost (modrá)
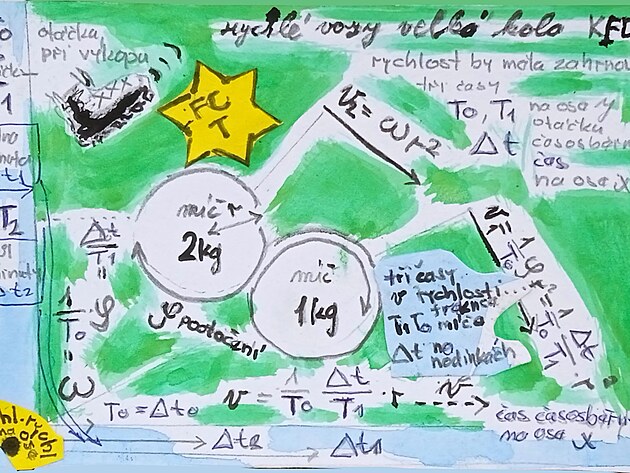
Proč některé fotbalové míče mají různou dráhu, když počáteční otáčky po výkopu jsou ty samé?
Proč některé fotbalové míče mají různou dráhu, když počáteční otáčky po výkopu jsou ty samé?
Příklad: jsou dány dva fotbalové míče.
Oba při výkopu mají ty samé otáčky - T0 - tato veličina se také nazývá perioda.
Míč 1 však má delší dráhu než míč 2.
Nebo jinak - na měřené vzdálenosti má míč 1 vyšší rychlost než míč 2.
Zde se vlastně sleduje jednak matematická funkce a jednak časosběrná změna matematické funkce.
Rychlost míče (pokud by se počítala přímo z otáček míče a nikoli statisticky dráha lomeno čas) - tedy rychlost by měla hodnotu (1 lomeno perioda neboli inverzní perioda první přesněji nulté otáčky T0 čili frekvence) krát úhlová dráha míče při otáčce T0 krát poloměr r na druhou - zkráceně: tzv. "úhlová rychlost na ose" krát poloměr r na druhou.
Po výkopu míčů by ovšem na sledované vzdálenosti - nebo časovém intervalu DELTA t - měl míč 1 nižší rychlost než míč 2... současně by měl menší otáčky - tedy by tento míč opsal kratší úhlovou dráhu než míč 2.
Jak je to možné? Míč 2 by měl vyšší hmotnost (například 2kg) než míč 1 o váze 1kg - a tato vyšší hmotnost by vlastně udržovala pro míč 2 vyšší rychlost - a pokud by na zkoumané dráze se míč kotálel vyšší rychlostí - znamenalo by to - že opsal vyšší úhlovou dráhu.
Ve výpočtech jsou tedy zastoupeny vlastně dva až tři časy které jsou součástí matematické funkce - rychlosti - a to čas T0 pro počáteční otáčky obou míčů a čas T1 a T2 jako doba rozdílné otáčky míče 1 a 2 na zkoumané vzdálenosti.
Časy T0, T1 a T2 jsou součástí matematické funkce - a matematická funkce se odečítá na ose "y". Ve výpočtech se ovšem vyskytuje ještě jeden podstatný čas - a to čas na stopkách či hodinkách - kterými se měří čas kterým míče trvá se dokotálet na předem stanovenou měřenou vzdálenost. Tento čas na stopkách se ovšem zobrazuje na časosběrné ose x - a ve výpočtech se označuje jako DELTA t.
Shrnuto: ve výpočtech se vyskytují dva čas na ose "y" jako součásti funkce - a to počáteční otáčka míčeT0 a doba otáčky T1/T2 na měřeném intervalu a pak čistě časosběrný čas DELTA t na ose "x".
Tyto dva časy - perioda T jako součást matematické funkce na ose "y" a časosběrný rozdíl DELTA t na ose "x" vlastně vymezujjí dvě osy kartézských souřadnic (čistě teoreticky perioda by vlastně mohla být administrativně pootočená z osy x do osy y) - alo rozčlenění otáčky - periody T a časosběrného intervalu do obou os zajisté něco vysvětluje.
Proč žlutá šesticípá Davidova hvězda s nápisem "FCT"? Jako připomenutí například bezejmenných fotbalových utkání při internaci Židů v Terezíně.
1KFD/ kinematika - frekvence, perioda, úhlová dráha (fotbalového míče) - pokračování
fotbalový míč ovšem může nahradit koloběžka
kinematika a hnané vozidlo
jezdec takt šlapadel
f - frekvence - jedna sekunda poměřená proměnnou dobou otáčky (periodou) - bezrozměrná veličina - lze ji tedy přiřadit k ose kola
konstrukce pohonu
psí - úhlová dráha (úhlové pootočení) - přepočtená frekvence (vynásobená jednou sekundou) - která tvoří spolu s frekvencí něco jako dvojici pro další výpočty - rychlosti a výkonu - bezčasová a bezrozměrná veličina - jen úhlová míra
jízdnímu kolu (tedy bicyklu - či velocipédu) ovšem předcházela koloběžka
kinematika a koloběžka
na rozdíl od íízdního kola, motocyklu nebo automobilu - tedy vozidla stabilně poháhěného - měla pohyb založený poněkud na jiném principu - kdy pohon není spojitý, ale založený jen na občasné síle odrazu
pokud by se zkoumalo vozidlo bez pohonu - typu koloběžka, nebo fotbalový míč - pak pohyb zkoumaného vozidla bez pohonu - by ponejvíce definovala veličina úhlová dráha (tedy bez síly a frekvence)
podle aktuálních poznatků je mezi frekvencí a periodou větší rozdíl, než by se mohlo z počátku jevit
jinak - frekvence - pomyslné vykopnutí a roztočení fotbalového míče - a perioda - kdy se otáčky - například vykopnutého fotbalového míče snižují k nule...perioda zřejmě není jen inverzní veličina frekvence</p><p>lze předpokládat, že frekvence je prvoveličina (která zahrnuje i výchozí tlak - výkop fotbalového míče - tedy sílo) - kdežto perioda zahrnuje prodlužující se otáčky míče při kotálení úhlová dráha fotbalového míče
(k frekvenci výkopu) se přidá perioda (která se v průběhu „letu“ míče prodlužuje a takto lze spočíst úlovou dráhu míče – tzv. úhlovou rychlost „omega“ na ose – a potažmo i dráhu míče a dobu „letu“výkop míče z matematického hlediska by mělo jít něco jako předderivaci, s časem = 1 (což je ostatně interval kterým se poměřuje frekvence)
" úhlová dráha "psí" je tedy „čas děleno časem“ – zkoumaný čas DELTA t lomeno perioda T (doba otáčky) na začátku "
rozdíl frekvence a perioda
úhlová dráha rovněž zkoumána v příspěvku Mechanika A1/KFD - radián, druhy frekvence, sanitky a jejich rozjezd 1 - Blog iDNES.cz a úhel záběru plynu
rozdíl frekvence - amplituda - což je ovšem rovněž, a možná ještě více záležitost elektrotechniky
rozcestník frekvence, perioda, amplituda - mechanika i elektrotechnika
dalším příspěvkem - kde se porovnávají obdobné veličiny v různých oborech je příspěvek Co se děje kolem elektřiny 5/ na rádiových vlnách 6 - AC/DC napětí, frekvence, amplituda - Blog iDNES.cz který přináší především informace o veličinách vyskytujících se u rozhlasového vysílání - nicméně obdobné veličiny se rovněž vyskytují v mechanice
OBSAH
ukázka podstatných částí příspěvku
rozcestník auto Škoda
rozcestník kinematika
1KFD/ kinematika - frekvence, perioda, úhlová dráha (fotbalového míče)
rozcestník frekvence, perioda, amplituda - mechanika i elektrotechnika
2 KFD/ kinematika - frekvence, perioda, úhlová dráha, úhlová rychlost (přechodová veličina mezi kinematikou a dynamikou)
proč rychlé vozy mají velká kola
motocykly se závěsným motorem
odkaz na rozcestník výkon
2.3 KDF/DPM rozcestník pro přepočty "kinematika - dynamika - MECHANICKÉ KOLO"
3DPM/ dynamika výkonů a momentů a výsledné rychlosti
4DAV/ dynamika rychlosti a zrychlení - pohyb rovnoměrný, rovnoměrně a nerovnoměrně zrychlený
rozcestník "rychlost a zrychlení"- pohyb rovnoměrný, rovnoměrně a nerovnoměrně zrychlený
5/ příběh automobilky Laurin a Klement - Škoda auto
6/ velká kola - velká rychlost - nebo malá spotřeba
7/ autonomní vozidla
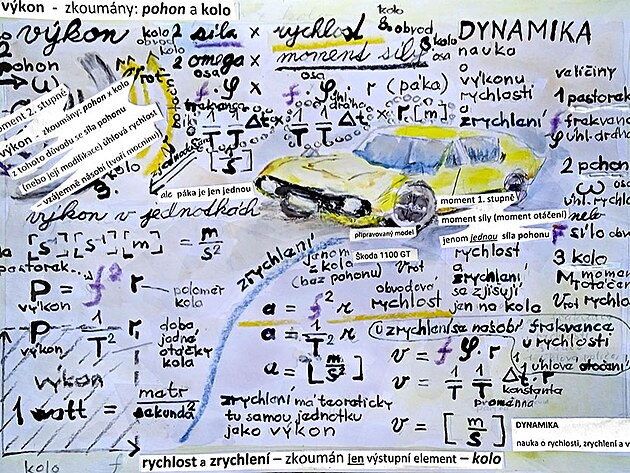
2 KFD/ kinematika rychlosti - frekvence, perioda, úhlová dráha, úhlová rychlost a lineární rychlost vozu (přechodová veličina mezi kinematikou a dynamikou)
/rychlost obvodová a celého vozidla by již měla být záležitostí oboru dynamika/
kinematika zkoumá mechanismus bez pohonu - tedy bez síly - zabývá se tedy především převodovými poměry - což je zejména velikost kol v celé soustavě (nikoli jenom v převodovce)
(číslice1,, 2, 3 značí zda se jedná o kinematiku pastorku - tedy kola č.1, o dynamiku pohonu - kola pohonu č.2 nebo o dynamiku kola vozu - tedy kola č. 3)
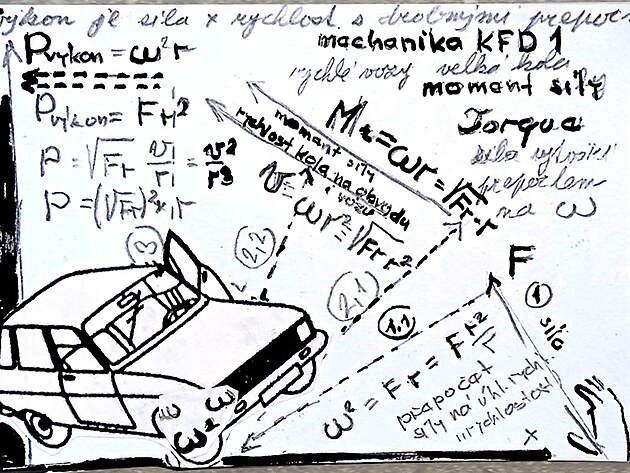
nejprve kinematika a následně dynamika - neboli od "řidiče po kolo vozu" - tedy veličiny frekvence a úhlové pootočení (přiřazené k prvnímu kolu převodu - pastorku) - přes dynamiku 2. kola - kola pohonu (úhlová rychlost na ose nebo variantně síla na obvodu) - až po dynamiku 3. kola - kola vozu (s veličinami buď moment otáčení s maximem na ose - nebo variantně s obvodovou rychlostí s maximem na obvodu
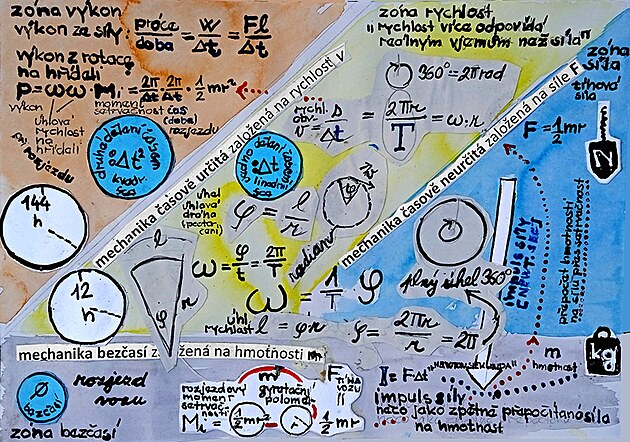
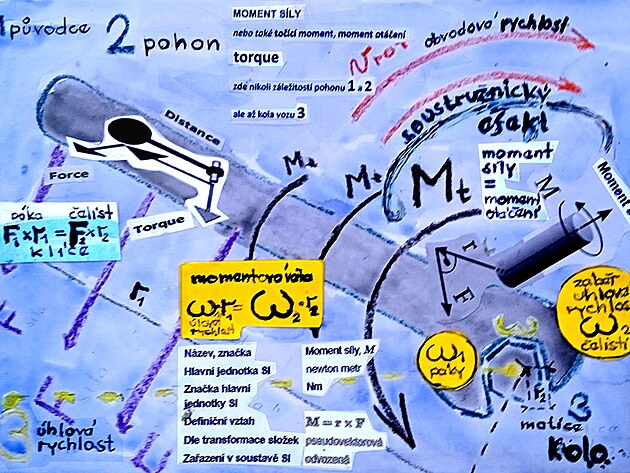
Z HLEDISKA MECHANIKY POHYBU je jako VÝHODNĚJŠÍ než veličinu SÍLA brát VELIČINU RYCHLOST - neboť RYCHLOST - ZEJMÉNA ROTAČNÍ (ostatně i proud trysky leteckého motoru má původ v rotaci - a to rotaci kompresoru) - z hlediska MECHANIKY, je tedy jako PŘESNĚJŠÍ BRÁT VELIČINU RYCHLOST - NEBOŤ RYCHLOST JE RYTMIZOVÁNA - MOŽNO ŘÍCI ČLENĚNA NA DÍLČÍ KINEMATICKÉ VELIČINY - JAKÝMI jsou MOMENT OTÁČENÍ "Torque "(který má stejný průběh od osy k obvodu - jak ostatně definuje MOMENTOVÁ VĚTA) - dalšími veličinami v posloupnosti je pak tzv. ÚHLOVÁ RYCHLOST OMEGA na ose hřídele - možná přesnější označení by bylo označení ZÁBĚR OMEGA - neboť záběr na ose zahrnuje jak veličiny RYCHLOST a SÍLA - ale nezahrnuje poloměr kola (ostatně úhlová rychlost OMEGA tak trochu připomíná pádlování třeba na kajaku - nebo kanoi) - tedy pomyslná střed záběru mezi konci pádla) - pokud by se v členění kinematických veličin postupovalo ještě dále - tak dalšími veličinami v posloupnosti níže pod ÚHLOVOU RYCHLOSTÍ OMEGA na ose hřídele by byly veličiny frekvence/perioda - veličina úhlová dráha "Fí" - která představuje něco jako natažení hodin - a která s největší pravděpodobností by byla jednou z cest přepočtu veličiny SÍLA na RYCHLOST - druhou cestou by měl být přepočet rychlosti a síly přes MOMENT OTÁČENÍ.
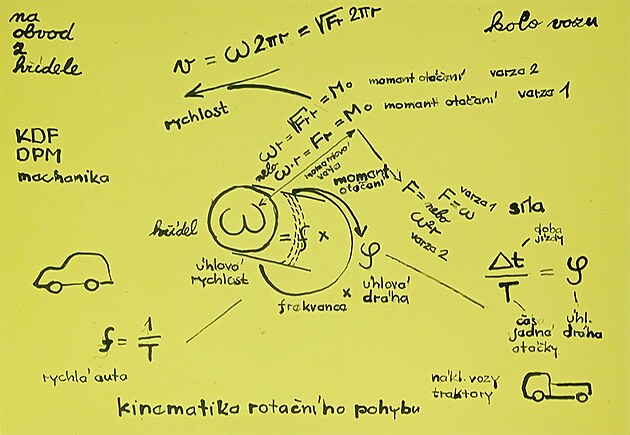
frekvence - perioda - úhlová dráha - úhlová rychlost
úhlová rychlost OMEGA jako součin frekvence a úhlové dráhy
úhlová rychlost "omega" je tedy frekvence na počátku krát úhlová dráha "psí"
úhlová rychlost "omega" je tedy frekvence na počátku krát frekvence ve zkoumaném čase lomeno perioda (doba otáčky) na počátku
což by mělo platit pro úhlovou rychlost s pohonem
jak by vycházela úhlová rychlost "omega" bez pohonu?
tedy například pro vozidlo pohybující se jenom setrvačností - jako třeba koloběžka
odhdhadem by vzorec mohl vycházet jako
úhlová rychlost na ose kola baz pohonu =úhlová rychlost s pohonem krát síla na počátku lomeno frekvence ve zkoumaném čase
pohyb kola (typu koloběžka - či fotbalový míč - pohybujícího se na základě jednorázového impulsu setrvačností) by vlastně měla definovat jen úhlová dráha krát frekvence (v čase na stopkách) krát perioda (při první otáčce)
u stabilně hnaného kola - třeba u bicyklu, nebo motocyklu, či automobilu by pohyb měla definovat ´tzv. úhlová rychlost na ose - daná součinem frekvence (v tomto případě úhlové k radiánu) a úhlové dráhy (či úhlového pootočení) - tato bezrozměrné veličiny definované jen úhlovou mírou
to byl pohled na mechaniku pohybu jakoby od osy - případně středu míče
při pohledu z obvodu míče - by veličina úhlová rychlost byla nahrazena veličinou úhlová dráha což je úhlová rychlost krát páka - i moment otáčení má ovšem "sídlo na ose"
jelikož všechno poměrně často bývá jinak - zdrojem momentu otáčení jakoby byla rychlost - a druhá zkoumaná veličina úhlová rychlost (na ose) - je zase ta samá veličina jako síla na obvodu - úhlová rychlost a síla se tedy liší jen působištěm
! malé upřesnění - úhlová rychlost omega má sídlo přímo na ose, ale moment síly/otáčení Mt
podle nejnovějších bádání moment síly by vlastně měla být dvousložková veličina (nebo dva momenty otáčení vzájemně násobené - první od "rukojeti" na osu otáčení F . r1 a druhý od osy otáčení k čelisti klíče omega . r2 .
"primární moment otáčení" rameno r1 - rukojeť osa klíče a matice
"sekundární moment otáčení" rameno r2 - osa matice a hrana klíče
pro souhrnný moment otáčení by měl platit vzorec
Mt = omega . r2 = odmocnina F.r1 x r2
momentem otáčení / síly se však více zabývá příspěvek Mechanika DPM1 - Výkon, nebo točivý moment - proč má traktor velké zadní kolo a je pomalý? - Blog iDNES.cz
pokračováním přepočtů síla - rychlost je část 7 tohoto příspěvku
síla a frekvence
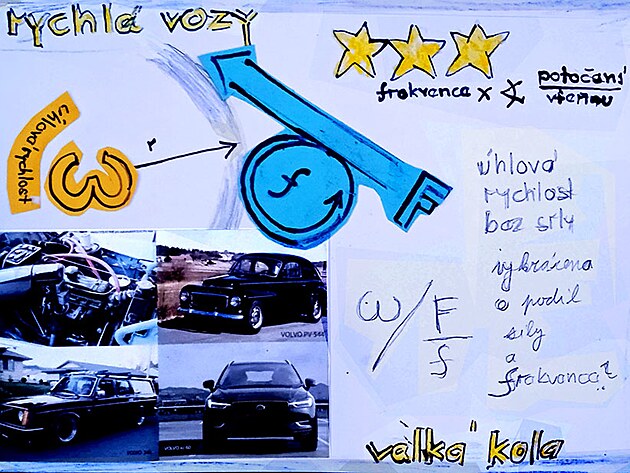
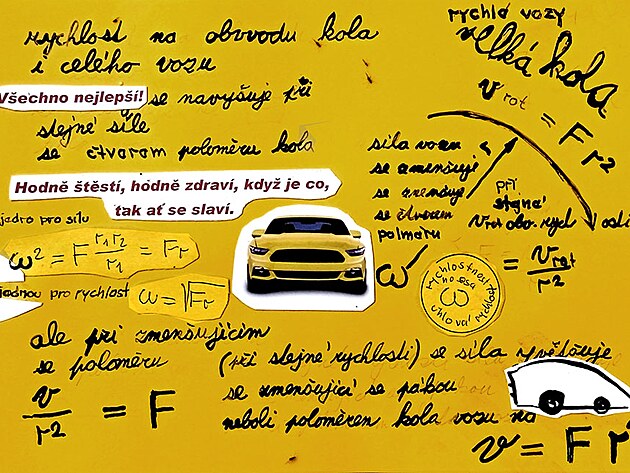
proč rychlé vozy mají velká kola
rychlost se přenáší na silnici z vozu prostřednictvím kola (3) a tahače mají obvykle několik robusních kol o malém průměru (vyjímkou je traktor) a se zvětšujícím průměrem kola se zvětšuje poloměr kola
motocykly se závěsným motorem
síla F - potažmo úhlová rychlost OMEGA na ose hřídele je u rychlých vozů tvořena vysokou frekvencí ale relativně malou úhlovou dráhou – zatímco u nákladních vozů a traktorů má malou frekvenci a velkou úhlovou dráhu
Rychlost vozu jako celku z průměrné rychlosti dráha lomeno čas delta t a rychlost vozu na základě otáčky kola o periodě T (ve výpočtech se vyskytují dva různé časy delta T – doba jízdy nebo zkoumaná doba jízdy a perioda či otáčka kola).
OBSAH
ukázka podstatných částí příspěvku
rozcestník auto Škoda
rozcestník kinematika
1KFD/ kinematika - frekvence, perioda, úhlová dráha (fotbalového míče)
rozcestník frekvence, perioda, amplituda - mechanika i elektrotechnika
2 KFD/ kinematika - frekvence, perioda, úhlová dráha, úhlová rychlost (přechodová veličina mezi kinematikou a dynamikou)
proč rychlé vozy mají velká kola
motocykly se závěsným motorem
odkaz na rozcestník výkon
2.3 KDF/DPM rozcestník pro přepočty "kinematika - dynamika - MECHANICKÉ KOLO"
3DPM/ dynamika výkonů a momentů a výsledné rychlosti
4DAV/ dynamika rychlosti a zrychlení - pohyb rovnoměrný, rovnoměrně a nerovnoměrně zrychlený
rozcestník "rychlost a zrychlení"- pohyb rovnoměrný, rovnoměrně a nerovnoměrně zrychlený
5/ příběh automobilky Laurin a Klement - Škoda auto
6/ velká kola - velká rychlost - nebo malá spotřeba
7/ autonomní vozidla
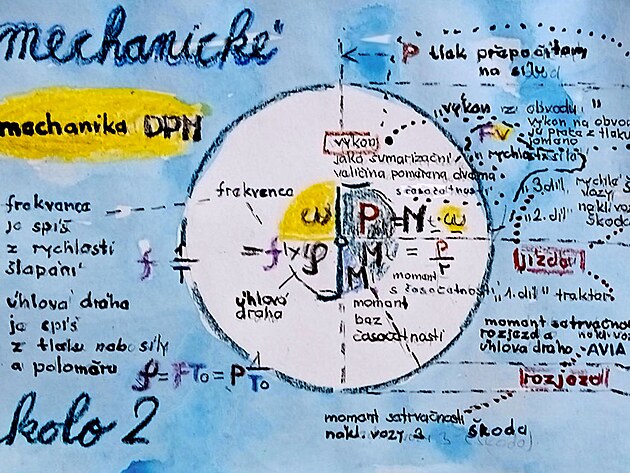
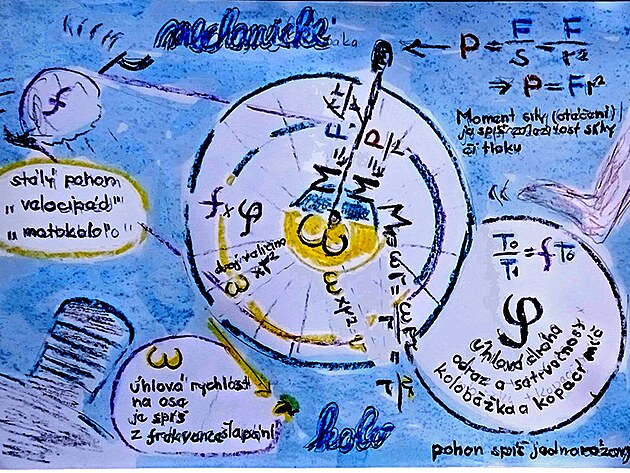
2.3 KDF/DPM rozcestník pro přepočty "kinematika - dynamika" přepočtový kotouč – mechanické kolo
přepočet sil, momentů, rychlostí na ose i na obvodu a výkonu (mechanika DPM) na kole vozu i celém vozidle
přepočet z hřídele na obvod
"mechanické kolo" - přepočtový kotouč kinematika - dynamika
! malé upřesnění - úhlová rychlost omega má sídlo přímo na ose, ale moment síly/otáčení Mt
by podle nejnovějších bádání měl moment síly být vlastně dvousložková veličina (nebo dva momenty otáčení vzájemně násobené - první od "rukojeti" na osu otáčení F . r1 a druhý od osy otáčení k čelisti klíče omega . r2 .
"primární moment otáčení" rameno r1 - rukojeť osa klíče a matice
"sekundární moment otáčení" rameno r2 - osa matice a hrana klíče
pro souhrnný moment otáčení by měl platit vzorec
Mt = omega . r2 = odmocnina F.r1 x r2
momentem otáčení / síly se však více zabývá příspěvek Mechanika DPM1 - Výkon, nebo točivý moment - proč má traktor velké zadní kolo a je pomalý? - Blog iDNES.cz
přepočet síla/moment síly - rychlost
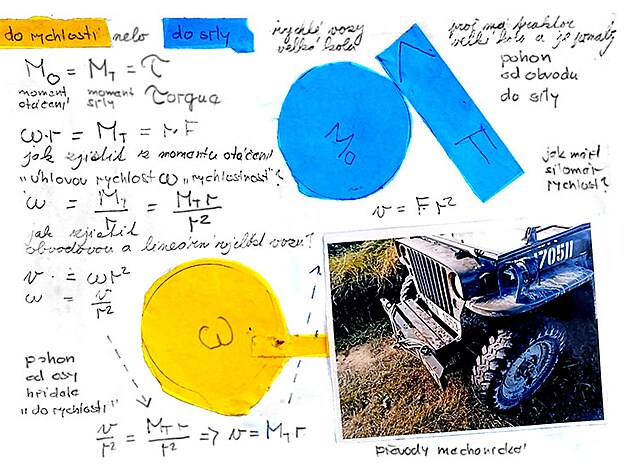
klíčový přepočet - proč rychlé vozy mají velká kola by zněl
F (síla) = v (rychlost) / r (poloměr)
velká síla = velká rychlost
ale p
potřebná síla lze zmenšit zvětšením poloměru kola => VELKÁ KOLA = rychlé vozy
nicméně moment otáčení lze vypočítat stejně z rotace (úhlové rychlosti OMEGA) na hřídeli - stejně ze síly F na obvodu kola - obě veličiny OMEGA a obvodová síla se vlastně liší jen svou pozicí - a ničím dalším - tuto pozici vymezuje poloměr "r", který ovšem není přímou součástí těchto veličiny - úhlové rychlosti OMEGA - ani síly na obvodě
je možné že platí něco jiný rub a jiný líc
přepočet rychlost / síla na obvodě
F(síla) =v(rychlost) /r (poloměr)
přepočet moment otáčení na hřídeli / rychlost na obvodě
Mt (moment otáčení na ose) = r (poloměr) x v (rychlost)
převod do síly
nebo převod do rychlosti ?
Je jistý rozdíl, jedná li se o převod z osy - nebo o převod z obvodu - například zuby ozubených kol vně.
Pokud je převod z obvodu - pak by se mělo jednat o převod do síly, kdy na obvodu působí síla a na ose se vytváří moment síly, což je vlastně teprve výsledný čintel síly. V tomto případě by tedy mělo jít o převod do síly.
Pokud by se jednalo o převod z osy - pak by je k je poháněcím činitelem tzv. úhlová rychlost omega - zde také nazývaná rychlostnost - a v zásadě se jedná o podobnou veličinu jako síla - a pokud se vynásobí OMEGA poloměrem kola - vytvoří se moment síly. Problém je ovšem, že moment síly působí na ose, stejně jako OMEGA. Bylo by tedy z hlediska posloupnosti správné přepočíst moment otáčení neboli síly přes obvodovou rychlost. Jelikož při zdrojem pohybu převodu z osy je úhlová rychlost - pak by prvotně vlastně mělo jít o převod do rychlosti - pokud vychází z osy.
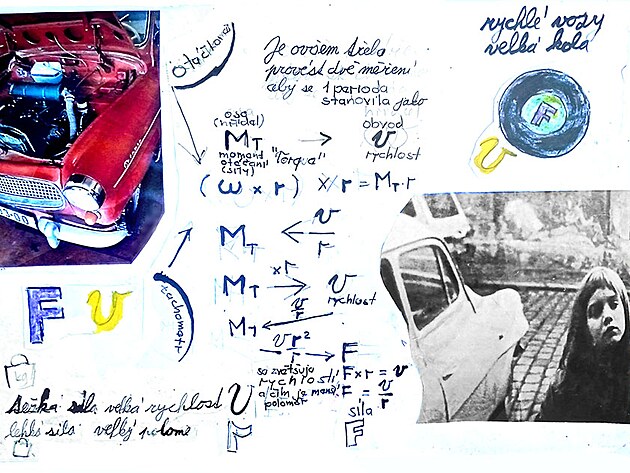
Pokud známe sílu a poloměr - je tedy možno spočítat moment síly (otáčení, angl. Torque) jak vypočítat úhlovou rychlost OMEGA na ose a obvodovou rychlost na obvodu - což je současně i výsledná lineární rychlost celého vozu?
Vzorec vychází z rovnosti momentu otáčení/síly pokud se počítá ze síly i úhlové rychlosti OMEGA, Jenomže pokud se počítá ze síly - tak se poloměrem nejprve násobí - a pokud by se z momentu otáčení měla zjistit úhlová rychlost - pak se naopak dělí...
Po vykrácení by pro přepočet síly na rychlost měl vyjít následující vzorec...
rychlost v = síla F krát poloměr r na druhou...
rozcestník výkon
Veličinou výkon se zabývá cyklus příspěvků mechanika DPM a také zejména jeden příspěvek z oboru letectví.
Pvýkon = Fsíla x r (poloměr) na druhou
výkon P je v principu (a ne zcela přesně) rychlost v krát síla F
tedy Pvýkon = Fsíla x vrychlost s výhradami
Výkon je exponenciální matematická funkce - podobně jako frekvence nebo rychlost - které jsou základní matematickou funkcí - ovšem výkon je exponenciální funkcí - kde je čas zkreslen - z hlediska pozorovatele vně je ve výkonu čas "jakoby na druhou".
"výkon první díl" Mechanika DPM1 - Výkon, nebo točivý moment - proč má traktor velké zadní kolo a je pomalý? - Blog iDNES.cz
" výkon druhý díl" se zaměřením na přepočet veličin síla / práce Mechanika DPM 2/W čím se liší veličiny tlak - síla a práce? - nákl. vozy Škoda/Praga - Blog iDNES.cz nákladní automobily Škoda a Praga
"Výkon v letectví" Letecký tachometr a tah, rychlost a výkon proudového letounu , letiště Žatec a Mig 29 - Blog iDNES.cz část 5 odkazovaného příspěvku
3DPM/ dynamika výkonů a momentů a výsledné rychlosti
Moment síly, otáčení (neboli "Torque") - podle aktuálních úvah - není výsledná hodnota - ale rovnice zvaná "momentová věta" platná vlastně pro výpočet, či přepočet síly. Podstata momentové věty by měla spočívat právě ve stejné hodnotě momentu otáčení - a navíc tyto momenty otáčení (či síly) jsou vlastně dva - jeden na rameni (například klíče) a druhý na jeho čelisti. A tyto momenty by vlastně měly mít stejnou hodnotu...
F1 (síla na držadle klíče) krát r1 (rameno klíče) = F2 (síla na čelisti) krát r2 (poloměr závitu klíče)
alternativně
r1 (rameno klíče) krát OMEGA1 (úhlová rychlost neboli záběr) na společné ose otáčení pro rameno klíče) =
r2 (poloměr závitu klíče) krát OMEGA2 (úhlová rychlost neboli záběr) na společné ose otáčení pro čelist klíče
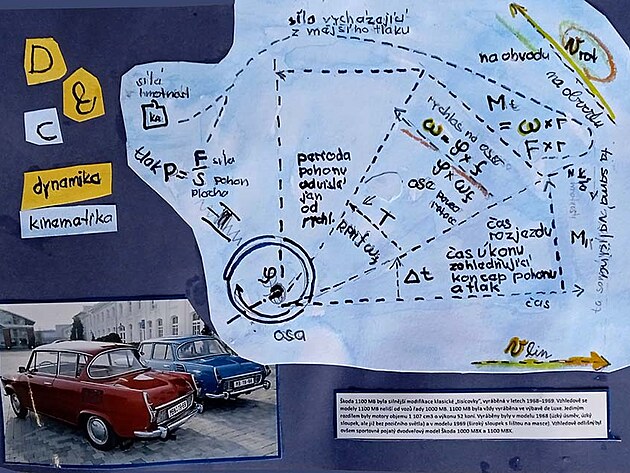
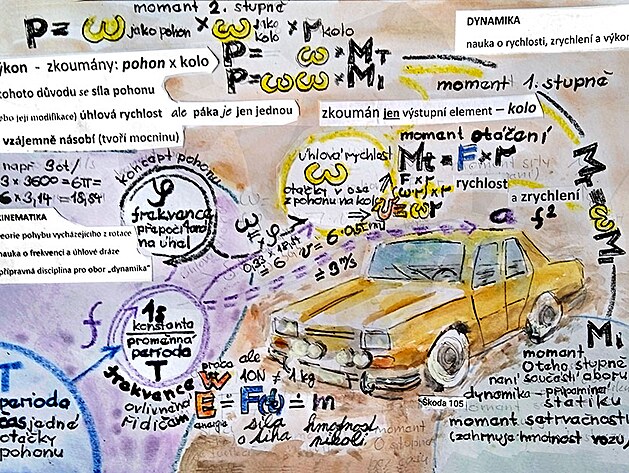
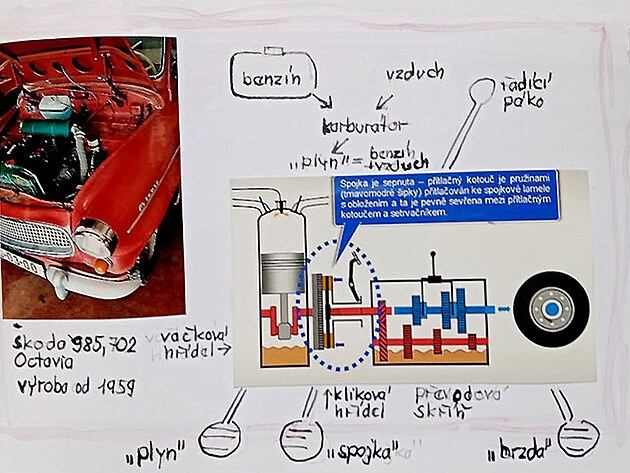
Škoda 1000 / 1100 MB
k nákresu níže
úhlová rychlost na ose kola - síla na ose až obvodu - rychlost na obvodu kola
moment setrvačnosti, otáčení a výkon na ose kola - síla rovnoměrně od osy po obvod kola
kinematika veličinami jsou frekvence, perioda, úhlové pootočení - a zejména úhlová rychlost (na ose) analyzuje různé druhy pohybu jako takového - ovšem bez reálných hodnot rychlosti a výkonu. že ize s jistým zjednodušením konstatovat - že kinematické veličiny jsou násobeny časem - a to časem konstrukčním - který se pohybuje od nuly do času daným rychlostí vozidla - v matematických výpočtech se toto násobení časem projevuje vlastně jako dělení - při zápisu do kartézských souřadnic by tento inverzní čas pro výpočet zkoumaných veličin jako by začínal hodnotou jedna na ose x - následně se měnil na hodnotu frekvence danou otáčkami rychlosti - a v zápisu do kartézských souřadnic se stáčel k ose y proti směru hodin - výkon zahrnuje frekvenci vlastně dvakrát - tedy i časem se dělí vlastně dvakrát
klíčovou veličinou v mechanice pohybu je moment otáčení - neboli síly " a násobkem s úhlovou rychlostí na ose - nebo násobkem rychlosti a síly na obvodu - se pak utváří další podstatnou veličinu pro mechaniku - což je výkon
| |||
| druhou | pákakrátsíla |
| |||
druhou
| pákakrátsíla |
úhlová rychlost na ose (neboli rotace, neboli rychlostnost je něco jako ekvivalent síly na obvodu - je ovšem zpravidla o něco menší než síla - jelikož se jedná v podstatě o odmocninu síly
převod - je spíš záležitost rychlosti a poměru mezi rotací ( nepřesně frekvencí) pastorku a druhého kola - pokud se uskutečňuje od osy - hřídele / ale spíše síly F - pokud se uskutečňuje z obvodu kola, například zuby ozubeného kola
druhý důvod, proč je převod spíš záležitost rychlosti - je pravidlo zachování rovnosti momentu síly na prvním i druhém kole převodu
výsledek je ovšem tentýž - moment síly, neboli otáčení, který má maximum na ose?
jak je to možné, když pro moment síly (otáčení) - který se počítá z obvodu podle vzorce síla krát páka platí vzorec úhlová rychlost omega krát páka? na ose je totiž nulová páka... snad jedině přepočtem přes obvodovou rychlost na kole (ta je ostatně stejná jako výsledná lineární rychlost celého vozu) - pokud se obvodová rychlost počítá přepočtem tzv. úhlové rychlosti od osy - pro obvodovou rychlost vychází (přibližně) čtverec poloměru - tedy omega x poloměr na druhou = obvodová rychlost "vé" - moment síly/otáčení - angl. Torque se pak tedy počítá zpětným přepočtem z rychlosti na obvodu - o po těchto přepočtech by měla pro moment otáčení/síly vyjít po vykrácení tentýž vzorec jako pokud by se počítal ze síly při pohonu zuby ozubených kol z vně
posloupnost veličin v kinematice a dynamice
Škoda 105 prototip
posloupnost veličin v kinematice a dynamice
OBSAH
ukázka podstatných částí příspěvku
rozcestník auto Škoda
rozcestník kinematika
1KFD/ kinematika - frekvence, perioda, úhlová dráha (fotbalového míče)
rozcestník frekvence, perioda, amplituda - mechanika i elektrotechnika
2 KFD/ kinematika - frekvence, perioda, úhlová dráha, úhlová rychlost (přechodová veličina mezi kinematikou a dynamikou)
proč rychlé vozy mají velká kola
motocykly se závěsným motorem
odkaz na rozcestník výkon
2.3 KDF/DPM rozcestník pro přepočty "kinematika - dynamika - MECHANICKÉ KOLO"
3DPM/ dynamika výkonů a momentů a výsledné rychlosti
4DAV/ dynamika rychlosti a zrychlení - pohyb rovnoměrný, rovnoměrně a nerovnoměrně zrychlený
rozcestník "rychlost a zrychlení"- pohyb rovnoměrný, rovnoměrně a nerovnoměrně zrychlený
5/ příběh automobilky Laurin a Klement - Škoda auto
6/ velká kola - velká rychlost - nebo malá spotřeba
7/ autonomní vozidla
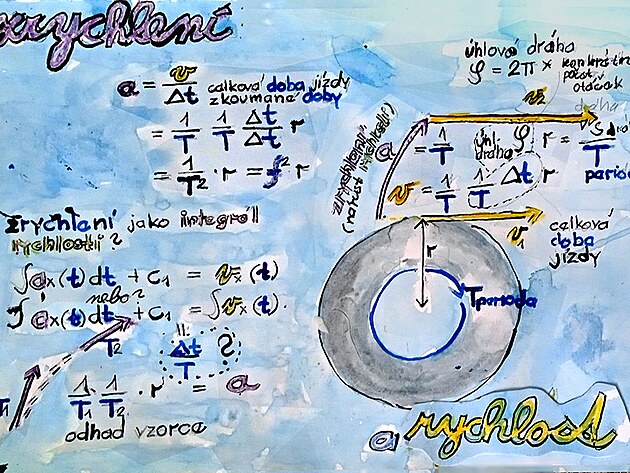
4DAV/ dynamika rychlosti a zrychlení
rozcestník zrychlení - mechanika DAV
Mechanika KFD 1 DAV - frekvence, rychlost, zrychlení / proč rychlé vozy mají velká kola (tento příspěvek)
úhlové zrychlení je definováni jako derivace úhlové dráhy podle času C2 Mechanika KFD 2 - pomalu a rychlo - běžný motor, cyklistické závody, druhy motopohonů - Blog iDNES.czz
nejprve veličina rychlost...
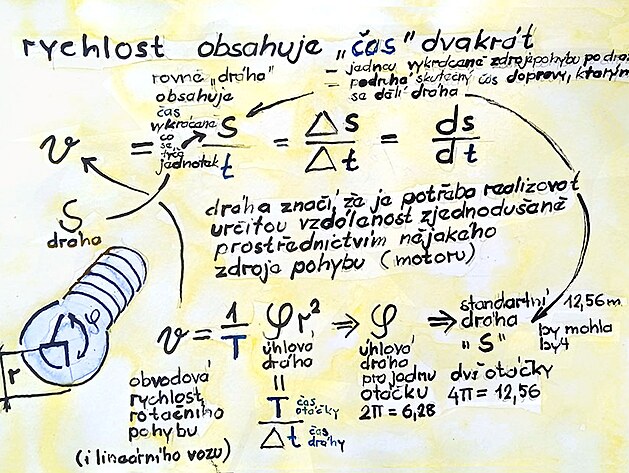
rychlost je charakteristika pohybu, která určuje, jakým způsobem se mění poloha tělesa v čase...
rychlost je definována jako dráha lomeno čas...
jenomže také veličina dráha - při podrobnějším zkoumání - může vyjít jako veličina která zahrnuje čas - a to dokonce dvojí - jednak čas potřebný k uskutešnění dráhy - tedy změny místa z bodu A do bodu B - a dále čas otáček pohonu (tedy motoru) - tedy periodu T motoru (dobu jedné otáčky) - nebo čas vyjádřený jako frekvence - například počet otáček za vteřinu - jednotky času se v čitateli a jmenovateli sice vykrátí - ale veličina čas je vlastně takto nepřímo - jako průvodní jev pohybu zastoupena zastoupena v dráze
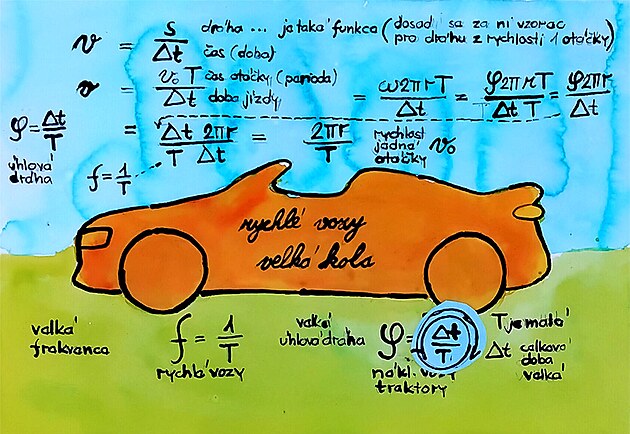
čím se liší osobní vozy a tahače z hlediska kinematiky? při stejné rychlosti kola nebo motoru mají rozdílnou úhlovou dráhu – osobní vozy mají relativně velkou frekvenci a malou úhlovou dráhu – traktory a tahače mají velkou úhlovou dráhu – tedy větší úhlovou rychlost na hřídeli (při stejné frekvenci)
podíl periody otáčky a času dráhy se nazývá úhlová dráha - a zpravidla se vyjadřuje nějakou jednotkou úhlové míry
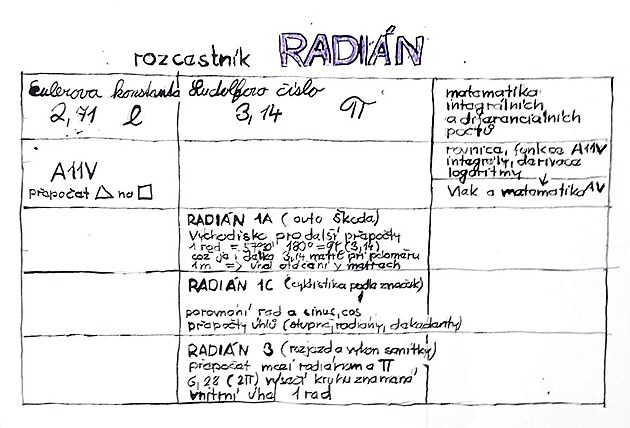
asi nejvýhodnější nejvýhodnější je vyjadřovat úhlovou míru prostřednictvím Ludolfova čísla neboť tato vyjádřenou obloukovou míru stačí vynásobit poloměrem - například kola automobilu - a z úhlové dráhy (vyjádřené úhlovou mírou) vznikne standartní dráha kterou vykoná vozidlo... (rychlé vozy mají vysokou frekvenci a malou úhlovou dráhu – zatímco nákladní vozy nebo automobily mají relativně malou frekvenci při velké úhlové dráze)
veličina zrychlení a veličina výkon zahrnují frekvenci (neboli inverzní čas vlastně dvakrát) - v obou případech je to však z jiného důvodu - zatímco v případě zrychlení jakoby veličina reálně zahrnovala dvojí periodu - jedna výchozí - a druhá perioda by měla zahrnovat měnící se periodu v užším smyslu - tak v případě výkonu má dvojí čas - přesně dvojí perioda jiný význam - podle všeho jedná se o kvadratickou rovnici - kde čas jakoby platil "na druhou" - je tedy jakoby "zahuštěnější" a vůči pozorovateli vně zkreslený - zatímco veličiny rychlost a zrychlení pozorovatel vně vnímá v reálném čase
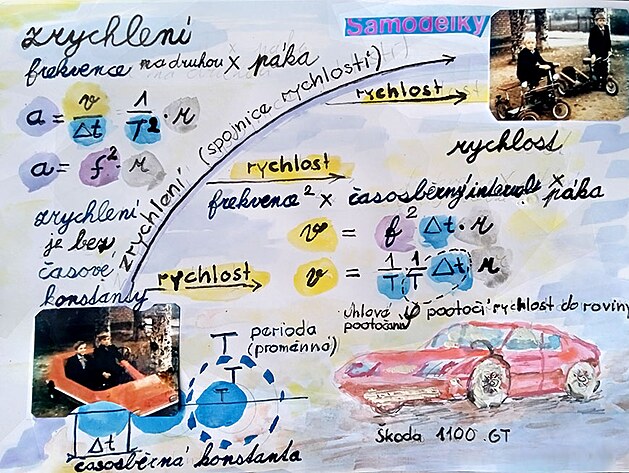
rychlost je frekvence (například kola vozu) násobená úhlovým potočením kola a poloměrem kola - lze tedy přepočítat na dráhu
Zrychlení se od rychlosti liší především - nezahrnuje dráhu (a to ani úhlovou dráhu - která vychází z poštu otáček) - a je ještě jednou děleno časem (konkrétně periodou jedné otáčky "kola") - zrychlení je vpodstatě poloměr kola dělený dvakrát periodou otáčky - přičemž možná poněkud nepřesně lze jednu periodu považovat za výchozí - když se pohyb začne zrychlovat - a druhou periodu by bylo možno považovat za periodu - kdy se zrychlování například vozidla ukončí - a pohyb vozu se opět stane rovnoměrným.
Škoda 1100 GT
Zrychlení je změna rychlosti (někdy taky označované jako změna změny - ale je otázka nakolik je toto označení výstižné), na rozdíl od rychlosti zrychlení chybí prvek dráhy .
Průměrné zrychlení objektu za určitou dobu je jeho změna rychlosti.
MOŽNÁ BY PRO ZRYCHLENÍ NEŽ ZMĚNA ZMĚNY BYL VÝSTIŽNĚJŠÍ POJEM "NEÚPLNÝ VÝKON"
Z hlediska matematiky se jedná o podíl k rychlosti, nebo dvojí podíl času k dráze.
Okamžité zrychlení
je limitem průměrného zrychlení v nekonečně malém časovém intervalu.
Z hlediska integrálních a diferenciálních počtů je okamžité zrychlení derivací vektoru rychlosti vzhledem k času, v nekonečně malém časovém intervalu.
Z hlediska integrálních a diferenciálních počtů jde o deravici druhého řádu k dráze. v nekonečně malém časovém intervalu.
rychlost přepočtem z frekvence otáčení kola (na podobném principu pravděpodobně funguje i tachometr)
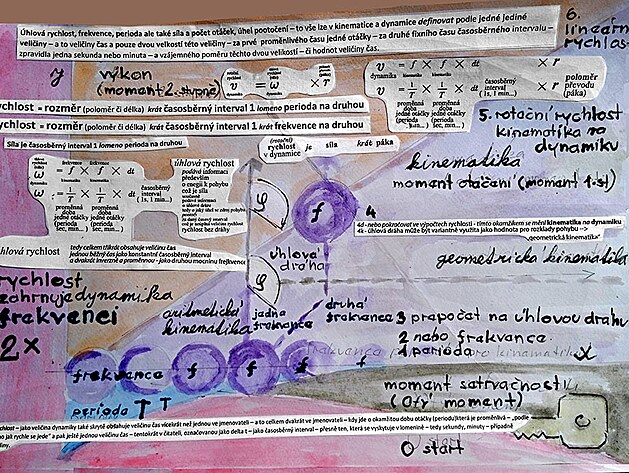
rozjezd (moment setrvačnosti - zde označen jako moment nultého stupně bez času, podobný momentům ve statice) - jízda (moment otáčení, rychlost, zrychlení - značené jako momenty 1. stupně) až po zjištění výkonu (zde označen jako moment 2. stupně
výpočet rychlosti na základě zrychleného pohybu
zde modifikovaný vzorec z kombinace vzorců - zejména vzorce dráha lomeno čas
při rovnoměrném pohybu by ve jmenovateli měla být hodnota jedna, která se v případě zrychleného pohybu zmenšuje - a naopak v případě zpomalování zvětšuje
pohyb může být rovnoměrný, rovnoměrně zrychlený a nerovnoměrně zrychlený
Výše je zobrazen přepočtový koeficient zrychlení - který vlastně supluje zrychlení přímo při výpočtu rychlosti (jelikož rychlost je jen jednou dělena časem) - tak tento přepočtový koeficient zrychlení jakoby byl něco jako zrychlení jednou dělené časem - a tento přepočtový koeficient by také bylo možno nazvat koeficient rychlosti pro pohyb rovnoměrný, rovnoměrně a nerovnoměrně zrychlený - a pro pohyb rovnoměrně přímočarý vychází jedna.
Mechanika KFD 1 DAV - frekvence, rychlost, zrychlení / proč rychlé vozy mají velká kola (tento příspěvek)
AV matematickým výpočtům typu rychlost, zrychlení. pohyb rovnoměrný a zrychlený je věnován spíše příspěvek Nádraží a vlak - rychlost a zrychlení - mechanika integrálních a diferenciálních počtů "AV - Blog iDNES.cz
OBSAH
ukázka podstatných částí příspěvku
rozcestník auto Škoda
rozcestník kinematika
1KFD/ kinematika - frekvence, perioda, úhlová dráha (fotbalového míče)
rozcestník frekvence, perioda, amplituda - mechanika i elektrotechnika
2 KFD/ kinematika - frekvence, perioda, úhlová dráha, úhlová rychlost (přechodová veličina mezi kinematikou a dynamikou)
proč rychlé vozy mají velká kola
motocykly se závěsným motorem
odkaz na rozcestník výkon
2.3 KDF/DPM rozcestník pro přepočty "kinematika - dynamika - MECHANICKÉ KOLO"
3DPM/ dynamika výkonů a momentů a výsledné rychlosti
4DAV/ dynamika rychlosti a zrychlení - pohyb rovnoměrný, rovnoměrně a nerovnoměrně zrychlený
rozcestník "rychlost a zrychlení"- pohyb rovnoměrný, rovnoměrně a nerovnoměrně zrychlený
5/ příběh automobilky Laurin a Klement - Škoda auto
6/ velká kola - velká rychlost - nebo malá spotřeba
7/ autonomní vozidla
5/ příběh automobilky Laurin a Klement - Škoda auto
Začalo to u "Hejtmánků" - což byl hostinec v Mladé Boleslavi - ještě za CK mocnářství
po vzniku republiky se z "Laurinky" stala firma "Škoda"
Opravna automobilů Škoda - Josef Procházka JIhlava
Škoda 706 R (nákladní vůz) a Škoda 706 RTO (nákladní automobil) již v poválečném období po roce 1945
následovaly osobní vozy model Sedan, Tudor, pak Spartak kterému se posléze podobala pozdější Octavia
Škoda 985, 70ě "Octavia" - výroba od roku 1959
závěr šedesátých let přines také specializaci jednotlivých členských států RVJP (Rada vzájemné hospodářské pomoci) - Československo se začlo specialzovat na modely outomomobilů s motorem vzadu (zatímco třeba v NDR se vyráběly "dvoutakty"...
pro "policejní službu" na dálnicích byla vytvořena speciální verze Škoda 110 R (zvaná R coupé)
OBSAH
ukázka podstatných částí příspěvku
rozcestník auto Škoda
rozcestník kinematika
1KFD/ kinematika - frekvence, perioda, úhlová dráha (fotbalového míče)
rozcestník frekvence, perioda, amplituda - mechanika i elektrotechnika
2 KFD/ kinematika - frekvence, perioda, úhlová dráha, úhlová rychlost (přechodová veličina mezi kinematikou a dynamikou)
proč rychlé vozy mají velká kola
motocykly se závěsným motorem
odkaz na rozcestník výkon
2.3 KDF/DPM rozcestník pro přepočty "kinematika - dynamika - MECHANICKÉ KOLO"
3DPM/ dynamika výkonů a momentů a výsledné rychlosti
4DAV/ dynamika rychlosti a zrychlení - pohyb rovnoměrný, rovnoměrně a nerovnoměrně zrychlený
rozcestník "rychlost a zrychlení"- pohyb rovnoměrný, rovnoměrně a nerovnoměrně zrychlený
5/ příběh automobilky Laurin a Klement - Škoda auto
6/ velká kola - velká rychlost - nebo malá spotřeba
7/ autonomní vozidla
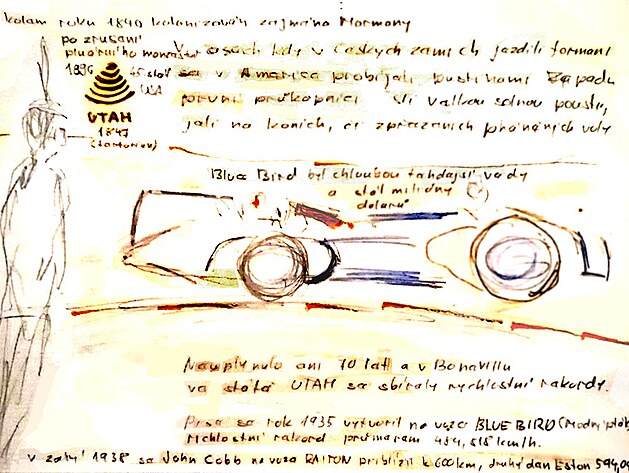
6/ velká kola - velká rychlost - nebo malá spotřeba + "přízraky na Solném jezeře"
Nápad soutěžit o co nejmenší spotřebu paliva se zrodil už v roce 1939 u olejářské firmy Schell v USA díky stejné společnosti o 30 let později. Od té doby udělala tzv. úsporná vozidla velký skok.
Tříkolka(Ultimate Fuel Optimiser) o hmotnosti pouhých 28 kg jako produkt firmy Ford, která se poprvé představila na známém automobilovém okruhu v Silverstonu, kde s ní 21 letá sekretářka Debbie Coleová dosáhla při průměrné rychlosti 24 km/h spotřeby 11 na 100km.
čtyřdobý vodou chlazený jednoválec z hliníku o objemu 15 ccm(23 x 33mm) s kompresním poměrem 13:1 s elektronickým vstřikováním paliva je totiž dílem vývojového oddělení Ford v Duntonu karoserie je vyrobena z karbonových vláken, má hmotnost 30 kg kola z kevralu obutá do cyklistických pneumatik a průměr 470 mm součinitel odporu vzduchu 13
Přízraky na Solném jezeře
OBSAH
ukázka podstatných částí příspěvku
rozcestník auto Škoda
rozcestník kinematika
1KFD/ kinematika - frekvence, perioda, úhlová dráha (fotbalového míče)
rozcestník frekvence, perioda, amplituda - mechanika i elektrotechnika
2 KFD/ kinematika - frekvence, perioda, úhlová dráha, úhlová rychlost (přechodová veličina mezi kinematikou a dynamikou)
proč rychlé vozy mají velká kola
motocykly se závěsným motorem
odkaz na rozcestník výkon
2.3 KDF/DPM rozcestník pro přepočty "kinematika - dynamika - MECHANICKÉ KOLO"
3DPM/ dynamika výkonů a momentů a výsledné rychlosti
4DAV/ dynamika rychlosti a zrychlení - pohyb rovnoměrný, rovnoměrně a nerovnoměrně zrychlený
rozcestník "rychlost a zrychlení"- pohyb rovnoměrný, rovnoměrně a nerovnoměrně zrychlený
5/ příběh automobilky Laurin a Klement - Škoda auto
6/ velká kola - velká rychlost - nebo malá spotřeba
7/ autonomní vozidla
7/ autonomní vozidla
Autonomní vozidla optimalizují trasy a snižují dopravní zácpy, integrují umělou inteligenci a vytvářejí bezpečnější, efektivnější a ekologičtější cestování.
Autonomní vozidlo "autonomous vehicle" by v podstatě mělo být auto řízené umělou inteligencí - nebo případně kombinací řidiče a automatického řidiče umělé inteligence (což by měl být smíšený provoz) - autonomní vozidla by vlastně mohla pozitivně přetvořit městskou krajinu.
Jan Tomášek
Dálniční most přes Křešické údolí 3 - kinematika stavebních strojů a stavba mostů

Jan Tomášek
Sněhový pluh KSP 411 / LPO 411 S - užitková železniční vozidla, uhlí a důlní lokomotivy
Jan Tomášek
Cesty energie 2E - jak platit za elektřinu QR kódem, elektřina, plyn a ekonomika, HE Most

Jan Tomášek
Matematická mechanika A0/ KFD 0 jak měří siloměr přes rychlost sílu / výpočty přes stopky
| Další články autora |

Exkluzivní nabídka prodeje stavebního pozemku v Olbramovicích - Slavkov
Olbramovice, okres Benešov
4 500 000 Kč
Střední školy
Nepřehlédněte
- Program, výsledky a postupový klíč Eura 2024: Češi padli s Portugalci, čeká je Gruzie
- Pavel ve středu na Hradě přivítá prezidenta Pellegriniho. Symbol usmíření, zní
- Šel po komkoliv, chtěl zabíjet, říká pobodaný motorkář z Argentinské
- Mustang slavil šedesátiny, do Kolína přiburácel i ten, co řídil Fittipaldi
- Od děcáku a drog k úspěchu. Každého klienta zšikanuju, i Jágra, říká holič slavných
- Fronty už od rána. Penny Market v Chodově opět otevřel, původní prodejna shořela
- Muž upoutal pozornost policisty. Při zásahu se u něj našly zbraně i munice
- V bytě vzplály nahromaděné odpadky, hasiči museli evakuovat sedm lidí