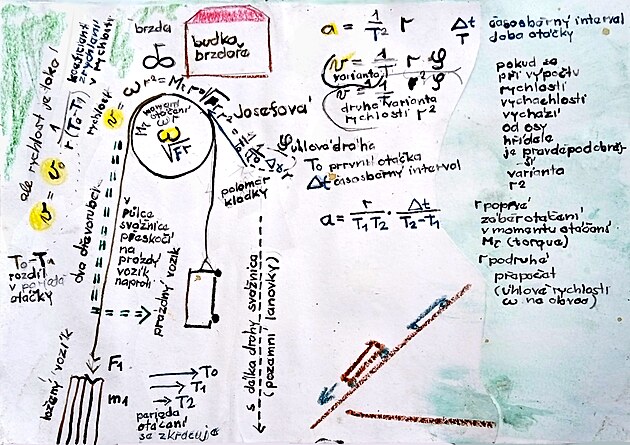
Matematická mechanika A0/ KFD 0 jak měří siloměr přes rychlost sílu / výpočty přes stopky

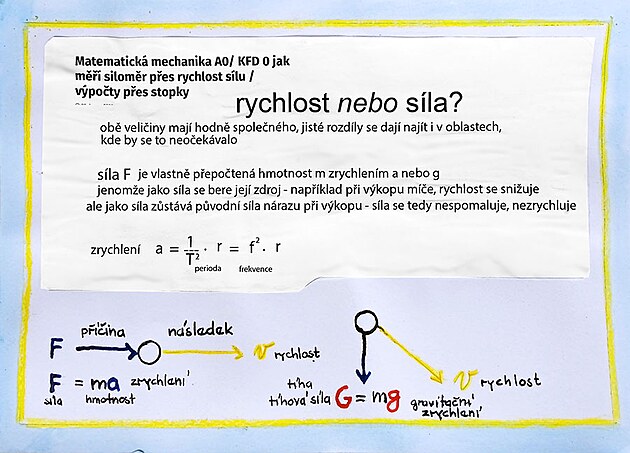
základními veličinami v mechanice pohybu je síla a rychlost - ovšem síla jakoby více zastupovala zdroj pohybu - rychlost zase vlastní mechanismus - z tohoto důvodu zde bude tendence převádět většinu veličin na rychlost 

Základními veličinami v mechanice pohybu je síla F a rychlost v - přičemž jako by spíš platilo buď síla - nebo buď rychlost - než síla a rychlost. Obě veličiny lze vzájemně přepočítat. Síla více vyjadřuje zdroj pohybu - veličina rychlost zase přesněji vymezuje pohyb z hlediska času - a to času jedné otáčky (ať už periody T, nebo frekvence f). V případě veličiny rychlost je tedy přesně daný matematický vztah rychlost - perioda jedné otáčky - což v případě veličiny síla tak jednoznačně dané není. Veličinu síla by bylo možno nazvat například jako například jako "veličina potřebná pro uvedení břemene o určité hmotnosti do pohybu" - a v tento matematický přepočet lze vyjádřit různými způsobu - kde čas nemusí figurovat vůbec, může figurovat jen jednou na bázi rychlosti - ale veličina "čas" může v těchto matematických přepočtech figurovat i dvakrát - a to na základě veličiny zrychlení - kde probíhá dělení časem na druhou.  

Síla s rychlost spolu tedy vzájemně velmi souvisí – kromě jiných odlišností jeden rozdíl je dost podstatný, k když to tak vypadat nemusí. Síla vyjadřuje příčinu, rychlost následek (z tohoto důvodu lépe podstatu pohybu vystihuje rychlost – zda se jedná o pohyb zpomalený – například vykopnutý míč – pohyb rovnoměrný, či zrychlený).

K ilustraci výše – vlevo pohyb po rovině, vpravo pohyb po nakloněné rovině.

Matematická mechanika  A0/ KFD 0 jak měří siloměr přes rychlost sílu / výpočty přes stopky a VUT Brno

 

 

OBSAH

VUT Brno
Rozcestník VUT Brno

přepočty 

část1 JAK MĚŘÍ SILOMĚR SÍLU  - rychlost nebo síla ?(první část)
Rozcestník matematika 
Rozcestník mechanika pohybu - kinematika a dynamika, rozcestník převody

část 2 rozbor měření - veličiny a jednotky času (dynamika, kinematika - a reálné vjemy)(člen převodu č. 1 pastorek) / kinematika - jako nauka o pohybu - frekvence a úhlová dráha (a dále pak dynamika - jako  nauka o rychlosti a výkonu- o dynamice však až v dalších částech příspěvku)

část 3 (člen převodu č. 1 pastorek) / kinematika - jako nauka o pohybu - frekvence a úhlová dráha (a dále pak dynamika - jako  nauka o rychlosti a výkonu- o dynamice však až v dalších částech příspěvku)
3s / výpočet frekvence a obvodové rychlosti na otáčejícím se kole jen s výpomocí "stopek"
JAK MĚŘÍ SILOMĚR SÍLU  (druhá část)

3pokračování/ výpočet frekvence a obvodové rychlosti na otáčejícím se kole jen s výpomocí "stopek"
část 4 (člen převodu č. 2 - kolo pohonu) / dynamika 2 - rotační rychlost, úhlová rychlost, síla, moment síly a siloměr  - přepočty kinematicko dinamických veličin

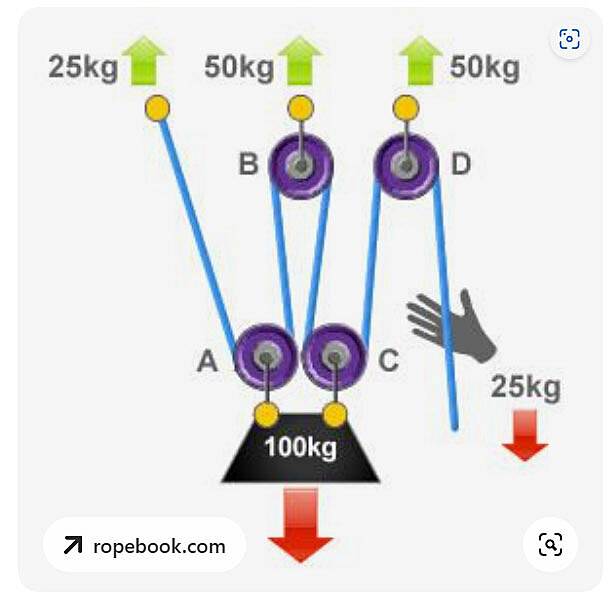
část 5 převody a kladkostroj

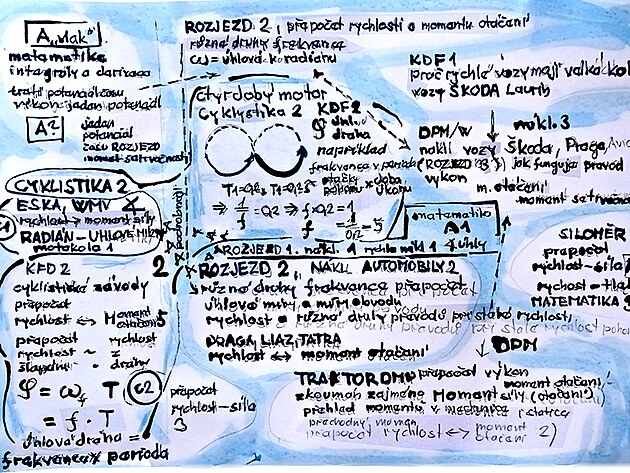
Otázka zní - dva hráči kopnou do dvou míčů - nebo udeří do koule kulečníku - na začátku se míče kotálí se stejnou frekvencí - jeden se však rychleji zpomalí - a druhý dokotálí dál ... proč to? - čímž by se měl zabývat sesterský příspěvek Mechanika KFD / DAV - frekvence, rychlost, zrychlení / proč rychlé vozy mají velká kola - Blog iDNES.cz (mechanické kolo 1)nebo obdobný příspěvek zaměřený na rozjezd nákladních vozů Mechanika DPM 3 /W výkon z tlaku, síly nebo práce? - nákladní vozy Škoda - Blog iDNES.cz (mechanické kolo 2)

VUT Brno

V roce 1847 byl založen německo-český vzdělávací ústav s dvojjazyčným názvem k. k. Technische Lehranstalt - c. k. technické učiliště. V roce 1873 se škola stala technickou vysokou školou. Bilingvní výuka však způsobila řadu obtíží, takže se zvýšily požadavky na samostatnou českou univerzitu. Dne 19. září 1899 podepsal císař František Josef I. (Rakousko-Uhersko) listinu o zřízení C. k. české vysoké školy Františka Josefa v Brně. V roce 1901 mu bylo uděleno právo udělovat doktoráty. Stavební inženýrství bylo prvním studijním oborem. První katedra pro elektrotechniku byla založena v Rakousku-Uhersku. Prvním a nejvýznamnějším mecenášem univerzity byl právník a politik Václav Robert Kounic, který v roce 1908 daroval vlastní městský palác jako studentskou kolej. Od roku 1918 nesla univerzita název České vysoké školy technické v Brně.

Od roku 1911 byla německá univerzita, která existovala ve stejné době, označována jako Císařská a královská německá technická univerzita. Existovala až do roku 1945.

Během německé okupace v letech 1939–45 byla Kounicova ubytovna nechvalně známou věznicí gestapa.

V roce 2000 došlo ve Zlíně k vyčlenění dvou fakult a vzniku Univerzity Tomáše Bati ve Zlíně.

Sídlem strojní fakulty byla v 70tých letech tzv. stará technika mezi ulicemi Údolní a Úvoz, ale to již se stavěla nová fakulta na Palackého vrchu, která byla postupně zprovozňována v letech osmdesátých.  

k nákresu výše - vlevo dole přiřazeny i "mimobrněnské příspěvky" vztahující se k opravně vozů Škoda Jihlava (společný rozcestník pro moment otáčení a opravnu vozů Škoda nížeji)

Na Palackého vrchu vyrostlo něco jako studijní městečko - kde výukový komplex doplňovaly dvoje koleje - Purkyňovy a Palackého - a řada menších provizorních budov - kde byly například laboratoře. 

rozcestník "VUT Brno"

matematika Rovnice, funkce, derivace, integrály, mocniny, odmocniny, exponenciály a logaritmy – Blog iDNES.cz

matematika Matematická mechanika  A0/ KFD 0 jak měří siloměr přes rychlost sílu / výpočty přes stopky a FS VUT (Strojní fakulta Vysoké učení technické v Brně)

elektrotechnika při FS VUT - měřící přístroje (Tesla Brno a Metra Blansko), koleje Palackého Co se děje kolem elektřiny 4 - osciloskop a měřící přístroje, Tesla Brno a Metra Blansko, tramvajová linka 12 - Blog iDNES.cz

elektrotechnika - měřící přístroje 2 Co se děje kolem elektřiny 7 - Ohmův zákon (2) a matematická funkce, osciloskop, Fakulta elektrotechnická VUT v Brně - Blog iDNES.cz

kinematika Dálniční most přes Křešické údolí 3 - kinematika stavebních strojů a stavba mostů - Blog iDNES.cz

telekomunikace V zajetí počítačů 6 "h" - jak zprovoznit počítač technicky, telekomunikační úřad Brno - Blog iDNES.cz

Zbrojovka a Zetor 1Mechanika DPM1 - Výkon, nebo točivý moment - proč má traktor velké zadní kolo a je pomalý? - Blog iDNES.cz

Zbrojovka a Zetor 2 (zemědělské stroje na Vysočině) Letní čtení na táboře a krásné staré zemědělné stroje - rozcestník Vysočina - Blog iDNES.cz

Zbrojovka a Zetor 3p - elektrické rozvody v továrnách Cesty elektrické energie 3p - rozvody a jištění v průmyslu (Zetor a Zbrojovka) - Blog iDNES.cz

část 1 JAK MĚŘÍ SILOMĚR SÍLU - rychlost nebo síla (první část)

Základními veličinami v mechanice pohybu je síla F a rychlost v - přičemž jako by spíš platilo buď síla - nebo buď rychlost - než síla a rychlost. Obě veličiny lze vzájemně přepočítat. Síla více vyjadřuje zdroj pohybu - veličina rychlost zase přesněji vymezuje pohyb z hlediska času - a to času jedné otáčky (ať už periody T, nebo frekvence f). V případě veličiny rychlost je tedy přesně daný matematický vztah rychlost - perioda jedné otáčky - což v případě veličiny síla tak jednoznačně dané není. Veličinu síla by bylo možno nazvat například jako například jako "veličina potřebná pro uvedení břemene o určité hmotnosti do pohybu" - a v tento matematický přepočet lze vyjádřít různými způsobu - kde čas nemusí figorovat vůbec, může figurovat jen jednou na bázi rychlosti - ale veličina "čas" může v těchto matematických přepočtech figurovat i dvakrát - a to na základě veličiny zryhlení - kde probíhá dělení časem na druhou.  

Jak ovšem rychlost a sílu vzájemně přepočíst?

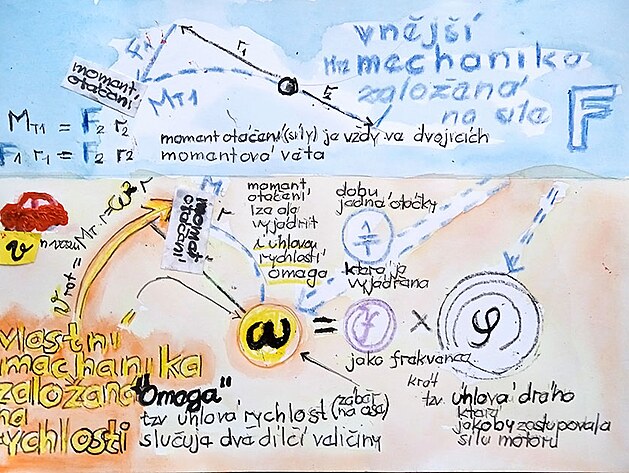
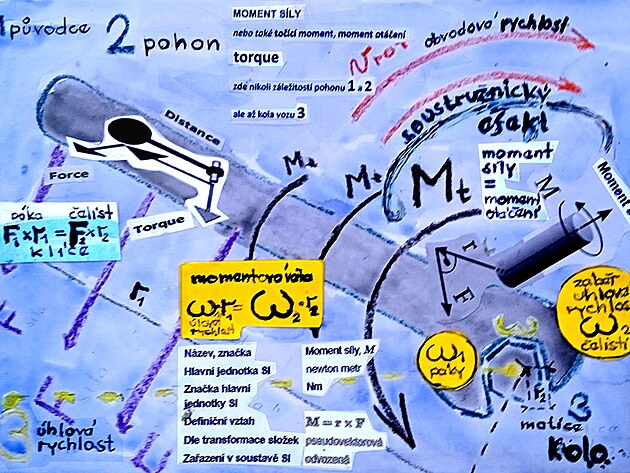
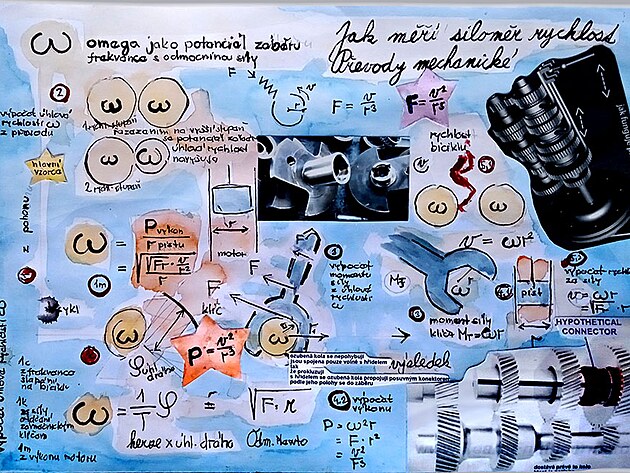
Spojnicí obou veličin by mohl být například moment otáčení (neboli moment síly). Moment otáčení - na rozdíl například veličiny rychlost není příliš názorná veličina - moment otáčení je spíš matematický přepočet či rovnice mezi výchozím působištěm například síly na rukojeti klíče - a působištšěm síly například na čelisti klíče. Jedna strana rovnice je výchozí síla krát rameno - druhá strana rovnice je účinná síla krát rameno. Moment otáčení lze ovšem vyjádřit nejen veličinou síla krát rameno - ale také veličinou "úhlová rychlost OMEGA" krát rameno neboli páka. Podstatný rozdíl je - že veličina síla má působiště na obvodu kola - ale úhlová rychlost OMEGA má působiště na ose hřídele, úhlová rychlost OMEGA má sice stejný pohybový účinek jako veličina síla - ale obě veličiny se liší působištěm.
Na základě předchozích výpočtů by tedy mezi ´veličinou síla na obvodu - a veličinou úhlová rychlost OMEGA na ose hřídele platit jistý matematický přepočet - a to přepočet daný vzorcem
F (síla) = OMEGA (úhlová rychlost) x r (poloměr) z čehož plyne OMEGA (úhlová rychlost) = F (síla) lomeno r (poloměr)

Obvodová (a také například lineární) rychlost celého vozu lze vypočítat podle následujícího matematického vztahu...
v = OMEGA x r na druhou (r je poloměr kola)

Rychlost na sílu by ovšem bylo možno přepočítat například přes moment otáčení  který lze vyjádřit jak veličinou síla F - tak veličinou úhlová rychlost OMEGA .

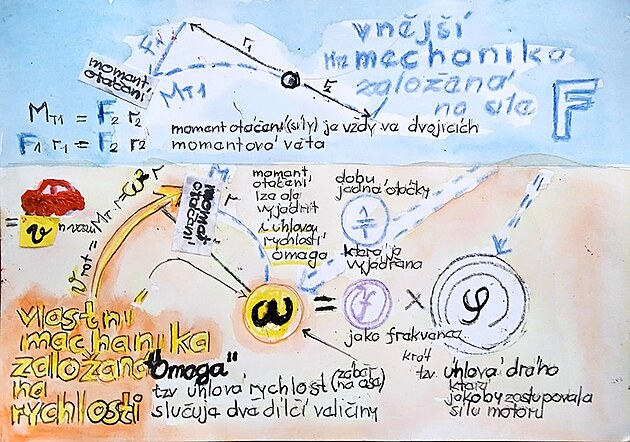
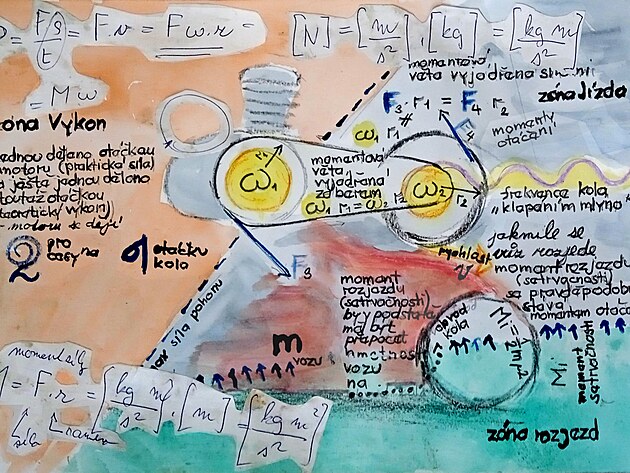
Momentová věta pro moment otáčení (moment otáčení neboli síly - jinak také Torque tvoří vždy dvojice sil - jedna síla například na "rukojeti" a druhá síla na "čelisti" klíče ) by zněla
Fxr = Fxr  nebo přesněji F1 xr1 = F2 xr2  

Síluna obvoduFovšem lze vyjádřit i tzv.úhlovou rychlostí OMEGAkterá má působiště na ose hřídele (vpodstatě se jedná o něco jako sílu ovšem s působištěm na hřídeli).

Pokud by se síla vyjádřila úhlovou rychlostí OMEGA na ose - pak by přepočetOMEGA-síla Fzně

F =OMEGAxr

a momentová věta vyjádřená úhlovou rychlostí OMEGA
by pak měla tvar  OMEGA1 x r1x r1 = OMEGA2 x r2 na druhou 

pokud by se do vzorce pro výslednou - obvodovou nebo lineární rychlost místo úhlové rychlosti OMEGA dosadila úhlová rychlost na ose hřídele vyjádřená veličinou síla (jak uvedeno ve vzorci výše) měl by vyjít následující vzorec 
v (rychlost obvodová i lineární celého vozu) = F (síla) krát r (poloměr)

nejprve malá anotace

veličiny síla a rychlost mají obdobnou podstatu - pře přepočtech v kinematice - dynamice - rychlost vychází z rotace - a síla zase z tlaku vně - jinak obě veličiny se v mechanice často  vyskytují dohromady - a  veličina výkon lze velmi zjednodušeně a nepřesně označit jako násobek síly a rychlosti

ovšem mezi veličinami síla a rychlost je jistý podstatný rozdíl - síla jako by zastupovala zdroj pohybu - fyzickou sílu cyklisty, tlak páry v parním  kotli a posléze tlak na píst u parní lokomotivy - nebo fázi "výbuch" ve spalovacím motoru - z tohoto důvodu jakoby síla zastupovala vnější zdroj pohybu - a veličina rychlost (případně její dílčí složky - perioda a frekvence) více představovaly vlastní mechanismus - z čehož plyne - veličinou mechaniky jako by spíše měla  být rychlost - a její dílčí složky, z tohoto důvodu zde bude tendence vyjadřovat matematicko - fyzikální vztahy v mechanice pohybu veličinou rychlost - vlastně všechny veličiny v mechanice pohybu lze vyjádřit obvodovou rychlostí (v některých případech na prvou - jako například tzv. úhlovou rychlost omega přímo na ose hřídele - nebo moment otáčení "torque" - pro který se rovněž používá označení moment síly (ale v případě mechaniky pohybu je výstižnější moment otáčení - dokonce možná stejně výstižné by bylo i označení moment rychlosti - podle základního vztahu pro moment rychlosti - což je omega krát poloměr - pokud by se úlová rychlost omega vyjádřila obvodovou rychlosti - pak by pro moment otáčení vyšel vzorec v obvodová rychlost lomeno poloměr) 

veličinami kinematiky jsou frekvence, perioda a úhlová dráha (úhlové pootočení) - kteréžto jednotky spolu vytváří něco jako dvojici - a pro další část mechaniky - což je dynamika

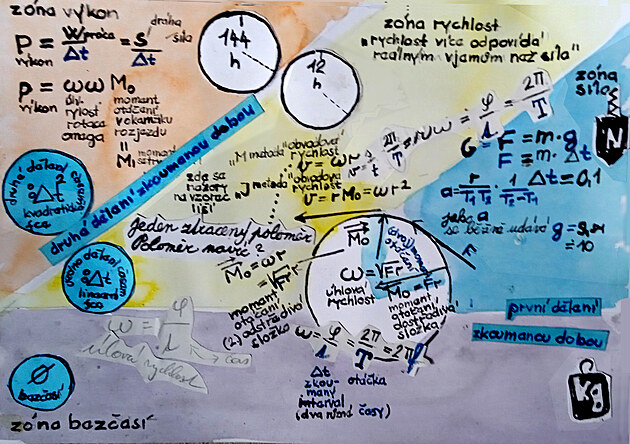
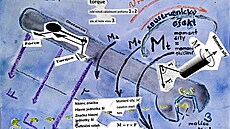
na nákresu výše - jsou dva podstatné vzorce - tedy výpočet síly z rychlosti a výkonu z rychlosti zobrazeny "ve hvězdičkách" 

poměrně důležitou veličinou  je úhlová rychlost na ose omega  - což je v zásadě tatáž veličina - jako síla F na obvodu, pokud je stroj poháněn ozubenými koly na převodu (ale jenom v zásadě - pro úhlovou rychlost na ose a sílu na obvodu platí jistý matematický přepočet)   - případně frekvence otáčení (pokud je přenos pohybu uskutečňován přes hřídel) plus nějaké další přepočtové koeficienty - které zahrnují vydatnost zdroje pohybu a zároveň hmotnost hnaného zdroje

úhlová rychlost na ose omega  - by se také dala nazvat třeba potenciál pohybu - a lze vyjádřit jak jednotkami inverzního času - sekundami na mínus prvou nebo neúplnou jednotkou síly - odmocninou newtonů 

tedy úhlová rychlost na ose omega  je vlastně veličina přes kterou lze přepočíst úplně všechny veličiny v mechanice - tedy například i rychlost a sílu 

jeden způsob jak vypočítat úhlovou rychlost na ose - a potažmo i obvodovou rychlost a rychlost celého vozu ze síly na obvodu - tedy přepočet síla - rychlost  

OMEGA = odmocnina (síla F na obvodu x poloměr r hnaného kola)

F na obvodu  =OMEGA na druhoulomeno poloměr r  = obvodová rychlost v na druhou lomeno poloměr r na pátou !!!!

pokud by se na podobném principu počítal výkon P (omega na druhou krát poloměr r) - po přepočtech a odmocňování by vyšel vzorec výkon P = obvodová rychlost v na druhou lomeno poloměr r na třetí !!!!

jiný způsob jak vypočítat úhlovou rychlost na ose - a potažmo i obvodovou rychlost a rychlost celého vozu ze síly na obvodu - tedy přepočet síla - rychlost  

u stabilně hnaného kola - třeba u bicyklu, nebo motocyklu, či automobilu by pohyb měla definovat ´tzv. úhlová rychlost na ose - daná součinem frekvence (v tomto případě úhlové k radiánu) a úhlové dráhy (či úhlového pootočení) - tato bezrozměrné veličiny definované jen úhlovou mírou

to byl pohled na mechaniku pohybu jakoby od osy - případně středu míče

při pohledu  z obvodu míče - by veličina úhlová rychlost byla nahrazena veličinou úhlová dráha  což je úhlová rychlost krát páka - i moment otáčení má ovšem "maximum na ose"

jelikož všechno poměrně často bývá jinak - zdrojem momentu otáčení jakoby byla rychlost - a druhá zkoumaná veličina úhlová rychlost (na ose) - je zase ta samá veličina jako síla na obvodu - úhlová rychlost a síla se tedy liší jen působištěm

přepočet veličin úhlová rychlost a moment otáčení (síly) na ose a síla a rychlost na obvodu

přepočty rychlost - síla, síla - rychlost

(dokončení v závěrečné části tohoto příspěvku, tedy části 7)

následovat by měly další pojmy kinematiky a dynamiky...

hlavními veličinami dynamiky jsou 

- rychlost

 - zrychlení

- výkon 

rychlost - tedy rotační rychlost byla nastíněna v předchozí části věnované siloměru - zde tedy alespoň stručně k dalším veličinám dynamiky - zejména veličině v ý k o n

 

OBSAH

VUT Brno
Rozcestník VUT Brno

přepočty 

část1 JAK MĚŘÍ SILOMĚR SÍLU  - rychlost nebo síla ?(první část)
Rozcestník matematika 
Rozcestník mechanika pohybu - kinematika a dynamika, rozcestník převody

část 2 rozbor měření - veličiny a jednotky času (dynamika, kinematika - a reálné vjemy)(člen převodu č. 1 pastorek) / kinematika - jako nauka o pohybu - frekvence a úhlová dráha (a dále pak dynamika - jako  nauka o rychlosti a výkonu- o dynamice však až v dalších částech příspěvku)

část 3 (člen převodu č. 1 pastorek) / kinematika - jako nauka o pohybu - frekvence a úhlová dráha (a dále pak dynamika - jako  nauka o rychlosti a výkonu- o dynamice však až v dalších částech příspěvku)
3s / výpočet frekvence a obvodové rychlosti na otáčejícím se kole jen s výpomocí "stopek"
JAK MĚŘÍ SILOMĚR SÍLU  (druhá část)

3pokračování/ výpočet frekvence a obvodové rychlosti na otáčejícím se kole jen s výpomocí "stopek"
část 4 (člen převodu č. 2 - kolo pohonu) / dynamika 2 - rotační rychlost, úhlová rychlost, síla, moment síly a siloměr  - přepočty kinematicko dinamických veličin

část 5 převody a kladkostroj

Co je námětem tohoto příspěvku...

MATEMATICKÁ MECHANIKA

mechanika pohybu - přesněji mechanika vozidla nebo jednoduchého mechanismu - jakým je například pružinový siloměr - přepočty veličin na obvodu - síla/rychlost a na hřídeli moment síly a úhlová rychlost.

nejprve však 

úvaha na téma používané veličiny a jejich zobrazování 

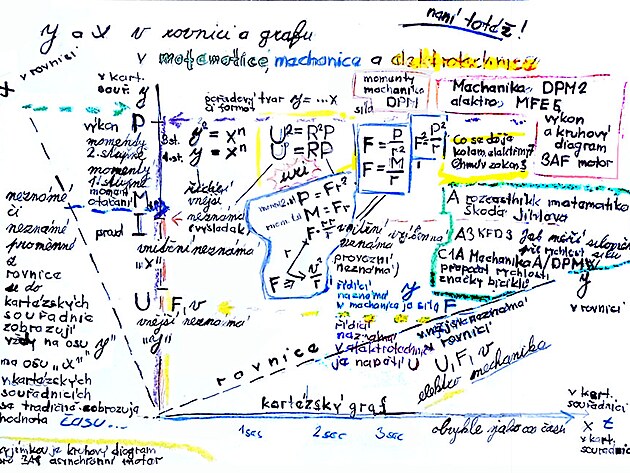
za výslednou veličinu lze v mechanice považovat sílu F - která plní stejnou roli jakou má "y" v rovnicích na levé straně  dalšími veličinami - které plní funkci "x" na pravé straně rovnice jsou pak moment otáčení (neboli síly) a jeho silnější varianta - tedy výkon, a za další skupinu veličin by bylo možno považovat různé varianty rychlostí v podobné roli jakou má například v rovnicích "z" - rovněž na pravé straně 

x a y v rovnici a grafu kartézských souřadnic není totéž

řídící neznámá "y"  a výkonná neznámá "x", tedy x a y jak se zapisuje v rovnici
a osy X a Y v  kartézských souřadnicích   není zdaleka totéž  - vlastně se jedná o dvě zcela odlišné záležitosti

neznámé z rovnice - a to jednak řídící (vnější souhrnná) neznámá "Y" a to jednak výkonné neznámé na opačné straně rovnice, případně i další neznámá z - se v grafu - neboli kartézských souřadnicích ve všech případech zobrazují na ose "Y" - či přesněji promítají se pod různými úhly - neboť jejich reálný průběh je někde v meziprostoru mezi osami y a x 

jednotlivé sledované veličiny - tedy neznámé y, x, případně z jako funkce v prostoru xy mají různou strmost - přičemž nejméně pozvolná je výsledná (řídící či vnější) funkce "Y" - což je c elektrotechnice zpravidla napětí U, v mechanice zase síla F - vnitřní neznámé z rovnice - tedy neznámé "X" mají zpravidla strmější průběh - v elektrotechnice se zpravidla jedná o proud nebo výkon - v mechanice zase moment otáčení (neboli síly) a výkon 

a následně již hlavní námět příspěvku

tedy MATEMATICKÁ MECHANIKA - přepočty veličin obvod - hřídel, síla moment síly, síla - rychlost a tak dále...

 

ROZCESTNÍK MATEMATIKA 

vnitřní matematika – matematika přepočtů

	Mechanika A/ KFD : kinematika (frekvence), dynamika (úhlová a obvodová rychlost) - Škoda - Blog iDNES.cz
	A11V Eulerova konstanta, integrály a derivace (Co se děje kolem matematiky 11) - Blog iDNES.cz
Avia“	Mechanika A3/KFD3 - radián, druhy frekvence, rozjezd a výkon sanitky - Blog iDNES.cz
přepočtyúhlů,––,	C1 Mechanika A/DPMW: stupně, Ludolfovo číslo radiány - přepočet rychlosti, značky bicyklů - Blog iDNES.cz

...a klíčový příspěvek - matematika a mechanika rychlosti a zrychlení Mechanika KFD / DAV - frekvence, rychlost, zrychlení / proč rychlé vozy mají velká kola - Blog iDNES.cz

vnější matematika – matematické funkce (i pro jiné obory)

	A11V Eulerova konstanta, integrály a derivace (Co se děje kolem matematiky 11) - Blog iDNES.cz
	Nádraží a vlak - rychlost a zrychlení - mechanika integrálních a diferenciálních počtů AV - Blog iDNES.cz
	Cesty elektrické energie a Ohmův zákon 2 - elektrárna Oslavany, Západomoravské elektrárny - Blog iDNES.cz
	Hallův efekt, matematika kosmických letů ; autoelektrika a elektromobil - Blog iDNES.cz
	"AVs" Matematická zamyšlení aneb jak se sází brambory a vaří bramborový guláš - Blog iDNES.cz

matematika a výkon (mechanika A - DPMA) 

výkon a příkon Co se děje kolem elektřiny 3 - něco dalšího o diodách - Blog iDNES.cz

Nádraží a vlak - rychlost a zrychlení - mechanika integrálních a diferenciálních počtů - Blog iDNES.cz

výkon elektrického obvodu po zprovoznění spotřebiče  Co se děje kolem elektřiny 7 - Ohmův zákon pro zapojený obvod - funkce a integrál - Blog iDNES.cz

 

matematika a kybernetika 

Ac odkaz na rozcestník matematika a kybernetika  V zajetí počítačů, elektroniky a kybernetiky 4 - Blog iDNES.cz

Ac3 V zajetí počítačů 3 (matematická logika a technika, logická hradla logické funkce) - Blog iDNES.cz

konjukce (logický součin průnik) - hradlo "and"
disjunkce (logický součet) - hradlo "or"
Shefferova spojka (negace logického součinu)  - hradlo "nahd"

matematika

A vstupní příspěvek pro matematiku - se zaměřením na doplňkové výpočty (např. přepočet úlových měr, druhů frekvence) v mechanice pohybu Mechanika A/ KFD : kinematika (frekvence), dynamika (úhlová a obvodová rychlost - Škoda - Blog iDNES.cz

A0 hlavní příspěvek pro matematiku Mechanika A0/ KFD 0 rozcestník matematická mechanika a jak měří siloměr přes rychlost sílu, VUT Brno (tento příspěvek)

A3 různé druhy frekvence podrobněji a současně příspěvek nákladní automobily 1 (rychlá nákladní vozidla), či rozjezd vozidel 1 Mechanika A3/KFD - rychlá nákladní vozidla a jejich rozjezd (1) přepočty druhů frekvence - Blog iDNES.cz

A2 nákladní automobily 2 (Škoda a Praga) Mechanika DPM 2/W čím se liší veličiny tlak - síla a práce? - nákl. vozy Škoda/Praga - Blog iDNES.cz

AVS integrální a diferenciální počet  slovesně Matematické úvahy u sázení brambor - Blog iDNES.cz

AV integrální a diferenciální počet Nádraží a vlak - rychlost a zrychlení - mechanika integrálních a diferenciálních počtů "AV - Blog iDNES.cz

AV5,6 Co se děje kolem elektřiny 5.6/ na rádiových vlnách 6 - AC/DC napětí, frekvence, amplituda - Blog iDNES.cz

A11V integrální a diferenciální počet (II) a Eulerova konstanta, Ludolfovo číslo -  Eulerova konstanta, lichá - tedy neúplná funkce, pravá funkce, exponenciální funkce a její derivace, exponenciální funkce a logaritmická funkce, dvojnásobná exponenciální funkce a integrál Eulerova konstanta,rovnice, funkce, logaritmy (Co se děje kolem matematiky, fyziky a elektrotechniky 11) - Blog iDNES.cz

matematická logika a úvahy

pravé a nepravé dělení (porcování či krájení a poměřování) je předmětem třeba příspěvku 

A4s pravé a nepravé dělení (porcování a poměřování - lichá a sudá funkce ) Mechanika DAV(PM): Holešov - rychlost letounu Z 142 - okamžitá a statistická ,zrychlení - Blog iDNES.cz

Mechanika A/ DAV (PM) - rychlost a zrychlení - veličina "čas" jako dělitel - Blog iDNES.cz příspěvek se zabývá především analýzou dělitele jako matematického operátoru a kdy vzniká "pravé" a "nepravé" dělení

Mechanika - elektrotechnika MFE 5 - výkon - jako moment třetího stupně, kruhový diagram - Blog iDNES.cz  v původním příspěvku rovněž pojednáno pravé a nepravé dělení 

matematika - úhly a míry, goniometrické funkce

aritmetická geometrie   převody úhlů (Ludolfovo číslo, radián) - přepočty mezi různými druhy frekvencí (úhlová frekvence k radiánu, frekvence k celému úhlu, RPM  otáčky za minutu)  v  rámci příspěvků

(tři příspěvky zabývající se obdobným tématem - tedy přepočty matematických veličin a vzorců - které se uplatňují v mechanice pohybu - ve spojení s nějakým dalším tématem mechaniky pohybu - tedy kinematiky a dynamiky)

ROZCETNÍK KINEMATIKA a DYNAMIKA MECHANIKA POHYBU

Rozcestník mechanika frekvence a rychlosti KFD - linie frekvence - rychlost (linie kinematika - dynamika)

kinematika a dynamika 1

Mechanika KFD / DAV - frekvence, rychlost, zrychlení / proč rychlé vozy mají velká kola/ osobní automobily Škoda - Blog iDNES.cz Otázka zní - dva hráči kopnou do dvou míčů - nebo udeří do koule kulečníku - na začátku se míče kotálí se stejnou frekvencí - jeden se však rychleji zpomalí - a druhý dokotálí dál ... proč to? - čímž by se měl zabývat odkazovaný příspěvek, tedy zejména veličinami úhlová dráha a úhlová rychlost OMEGA.

dynamika 1

Mechanika DPM1 - Výkon, nebo točivý moment - proč má traktor velké zadní kolo a je pomalý? - Blog iDNES.cz

dynamika 2

Mechanika DPM 2/W čím se liší veličiny tlak - síla a práce? - nákl. vozy Škoda / Praga / Liaz - Blog iDNES.cz

kinematika 3

Mechanika A3/KFD - radián, frekvence, rozjezd a výkon sanitky, rozcestník Avia - Blog iDNES.cz

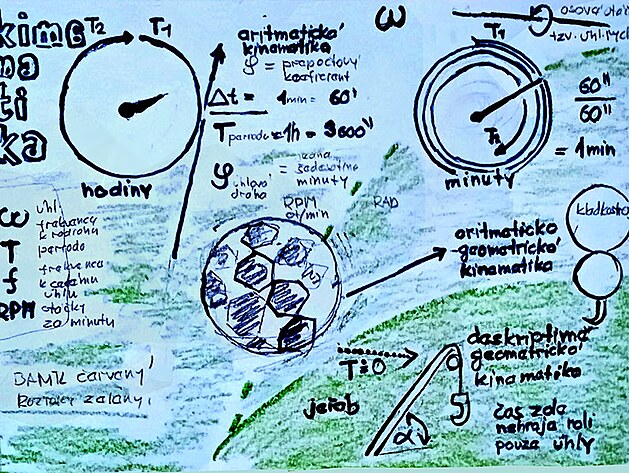
Rozcestník aritmeticko - geometrická kinematika

kinematika - členění

aritmetická kinematika - otáčky pohonu (například motoru automobilu)

aritmeticko - geometrická  kinematika - čas přepočtený na úhlovou dráhu - může mít význam například u výpočtu otáček kladkostroje; (aritmeticko) - geometrická kinematika například pro pohyb kladkostrojea  určité míry  i stavebních strojů j jeřábů  - kinematika která vychází z frekvence a hybnosti 

deskriptivně - geometrická  kinematika - čas zde nehraje roli - význam zde mají úhly mezi jednotlivými elementy a také počet stupňů volnosti příslušný ke každému elementu - typickým zařízením kde se uplatňuje tato disciplína jsou stavební stroje a jeřáby

jak se z aritmetiky stává geometrie ?

poměrně důležitou veličinu v mechanice je přepočet mezi časem a dráhou - což umožňuje veličina zvaná úhlová dráha psí

ve zlomcích se vykrátí (mezi čitatelem čas úkonu delta t a jmenovatelem veličina čas perioda otáčky T - nikoliv však hodnoty které se vypočítaly - a z otáček se stanou úhly - nicméně aritmetika je zde stále latentně zastoupena - proto zde použito označení aritmeticko - geometrická...Mechanika KFD / DAV - frekvence, rychlost, zrychlení / proč rychlé vozy mají velká kola - Blog iDNES.cz 

další disciplína - zde označená jako deskriptivně-geometrická kinematika je čistě geometrickou záležitostí 

podčást aritmeticko - geometrická kinematika 

v části 2 a 3 příspěvku je právě pojednán převod frekvence a rotace (úhlové rychlosti) - zde nazván jako geometrická kinematika (přesněji aritmeticko - geometrická kinematika - neboď zde stále aritmetické veličiny hrají jstou roli, na rozdíl u geometrických převodů lineárních pohybů na rotaci - zde označovaném jako  deskriptivně - geometrická kinematka

Mechanika JB /DPMW přístavní jeřáb - jak se připojit k internetu 4 (přirovnání k přístavu) - Blog iDNES.cz (část příspěvku na téma jeřáby)

(Dálniční most přes Křešické údolí 3 - kinematika stavebních strojů a stavba mostů - Blog iDNES.cz )

podčást deskriptivně - geometrická kinematika 

Mechanika KFD 4 - návštěva tiskárny a části strojů Návštěva staré tiskárny - části strojů a mechanismy - Blog iDNES.cz

Dálniční most přes Křešické údolí 3 - kinematika stavebních strojů a stavba mostů - Blog iDNES.cz

(Mechanika JB /DPMW přístavní jeřáb - jak se připojit k internetu 4 (přirovnání k přístavu) - Blog iDNES.cz)

 

Matematika ve strojírenství - rozcestník převody a jeřáby

Matematická mechanika  A0/ KFD 0 jak měří siloměr přes rychlost sílu / výpočty přes stopky - převody 1 (tento příspěvek)

Převody mechanické (kolo a pastorek) a elektrické (trafa) - vozy Mercedes a vojenství - Blog iDNES.cz

Návštěva staré tiskárny - části strojů a mechanismy - Blog iDNES.cz

Mechanika JB /DPMW přístavní jeřáb - jak se připojit k internetu 4 (přirovnání k přístavu) - Blog iDNES.cz mechanické výpočty pro jeřáb

OBSAH

VUT Brno
Rozcestník VUT Brno

přepočty 

část1 JAK MĚŘÍ SILOMĚR SÍLU  - rychlost nebo síla ?(první část)
Rozcestník matematika 
Rozcestník mechanika pohybu - kinematika a dynamika, rozcestník převody

část 2 rozbor měření - veličiny a jednotky času (dynamika, kinematika - a reálné vjemy)(člen převodu č. 1 pastorek) / kinematika - jako nauka o pohybu - frekvence a úhlová dráha (a dále pak dynamika - jako  nauka o rychlosti a výkonu- o dynamice však až v dalších částech příspěvku)

část 3 (člen převodu č. 1 pastorek) / kinematika - jako nauka o pohybu - frekvence a úhlová dráha (a dále pak dynamika - jako  nauka o rychlosti a výkonu- o dynamice však až v dalších částech příspěvku)
3s / výpočet frekvence a obvodové rychlosti na otáčejícím se kole jen s výpomocí "stopek"
JAK MĚŘÍ SILOMĚR SÍLU  (druhá část)

3pokračování/ výpočet frekvence a obvodové rychlosti na otáčejícím se kole jen s výpomocí "stopek"
část 4 (člen převodu č. 2 - kolo pohonu) / dynamika 2 - rotační rychlost, úhlová rychlost, síla, moment síly a siloměr  - přepočty kinematicko dinamických veličin

část 5 přepočty hmotnosti a síly a kladkostroj

následuje

vlastní příspěvek - pokračování

"A0" Mechanika KFD 0 - kinematika: frekvence - dynamika: síla, moment síly, rychlost a siloměr

 

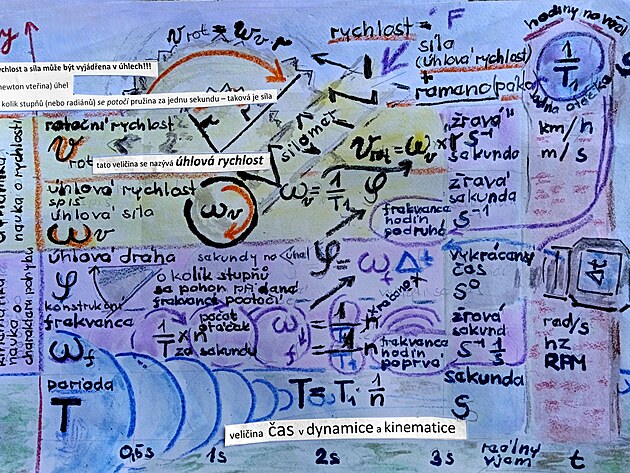
část 2/  kinematika, dynamika a reálné vjemy - veličiny a jednotky 

dynamika - veličiny

výsledná rotační rychlost = síla a páka

síla = úhlová rychlost (úhlová síla) x r (poloměr kola)  může to být například hodnota v inverzních sekundách odečtená na siloměru 

úhlová rychlost = úhlová dráha (kinematická frekvence pohonu) krát frekvence stopek (provozní frekvence stopek)

úhlová rychlost je také - co se měří na stopkách  - tedy naměřený čas DeltaT ,který se porovnává sfrekvencí stopek f1-přepočtenou na periodu T1 

dynamika - jednotky

většina jednotek je složených - například km/h nebo m/s ale vždy se zde vyskytuje inverzní jednotka času,

kterou lze nazvat třeba jako

inverzní - nebo dokonce  žravé sekundy na minus prvou 

kinematika

kinematika rozborů mechanismů, "geometrická" kinematika

zcela bez času 

úhlová dráha (z kinematická frekvence pohonu - počáteční  čas  otáčky v jmenovateli  a proměnlivý rozdíl periody jako čas ve sledovaném intervalu v čitateli) 

jednotky: (pokud je vyjádřeno algebraicky) - nějaká forma úhlové míry

"algebraická" kinematika, jako diciplína pro "předvýpočet" pro výsledky spadající již do části mechaniky  dynamika

"algebraická"kinematika - veličiny

frekvence - třeba stopek ( jako konstrukční - kinematická frekvence stopek)

/znovu budiž připomenuto - že frekvence stopek se ve výpočtech vyskytuje dvakrát - protože poprvé se vlastně jedná o kinematickou veličinu - frekvence poprvé ve výpočtech zde označena jako kinematická, čí konstrukční, teoretická frekvence - a podruhé ta samá veličina označena jako provozní frekvence/

"algebraická"kinematika - jednotky

podobně jako v dynamice se zde vyskytuje inverzní jednotka času,

kterou lze nazvat třeba jako

inverzní - nebo dokonce  žravé sekundy na minus prvou 

 Jak v dynamice - tak  kinematice vyskytují jednotky času ve jmenovateli zlomku - kilometry za hodinu, metry za sekundu, radiány za sekundu a tak dále...čemuž napovídá i inverzní charakter jednotek času ve frekvenci, úhlové rychlosti a rychlosti - na rozdíl od periodických zvuků v běžných, nikoli inverzních vteřinách - které doléhají k posluchači například na nástupiště

jednotky - shrnutí

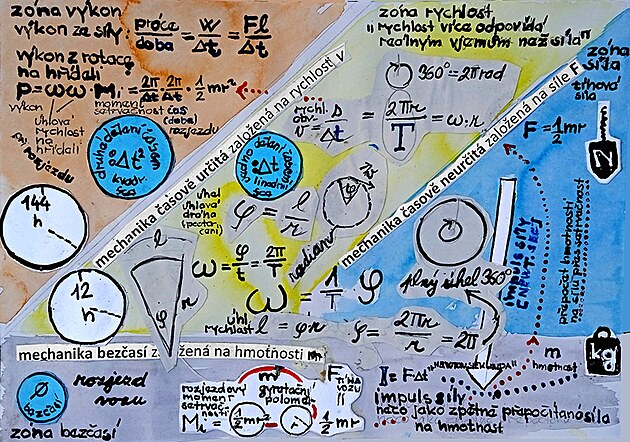
shrnutí jednotek ve všech zkoumaných oborech mechaniky - tedy dynamice, kinematice a reálném čase

dynamika - u zkoumaných veličin  rotační rychlost a úhlová rychlost (síla) jsou platnou jednotkou času tedy inverzní "žravé" sekundy na minus prvou

kinematika - u zkoumaných veličin  úhlová dráha jsou platnou veličinou úhly ve stupních t a frekvence, nebo úhlová frekvence - či otáčky za minutu RPM opět inverzní jednotky času - tedy například inverzní sekundy  

reálný čas - v reálném čase jsou jednotkami času například sekundy - jako jednotka časosběrné veličiny

 

OBSAH

VUT Brno
Rozcestník VUT Brno

přepočty 

část1 JAK MĚŘÍ SILOMĚR SÍLU  - rychlost nebo síla ?(první část)
Rozcestník matematika 
Rozcestník mechanika pohybu - kinematika a dynamika

část 2 rozbor měření - veličiny a jednotky času (dynamika, kinematika - a reálné vjemy)(člen převodu č. 1 pastorek) / kinematika - jako nauka o pohybu - frekvence a úhlová dráha (a dále pak dynamika - jako  nauka o rychlosti a výkonu- o dynamice však až v dalších částech příspěvku)

část 3 (člen převodu č. 1 pastorek) / kinematika - jako nauka o pohybu - frekvence a úhlová dráha (a dále pak dynamika - jako  nauka o rychlosti a výkonu- o dynamice však až v dalších částech příspěvku)
3s / výpočet frekvence a obvodové rychlosti na otáčejícím se kole jen s výpomocí "stopek"
JAK MĚŘÍ SILOMĚR SÍLU  (druhá část)

3pokračování/ výpočet frekvence a obvodové rychlosti na otáčejícím se kole jen s výpomocí "stopek"
část 4 (člen převodu č. 2 - kolo pohonu) / dynamika 2 - rotační rychlost, úhlová rychlost, síla, moment síly a siloměr  - přepočty kinematicko dinamických veličin

část 5 přepočty hmotnosti a síly a kladkostroj

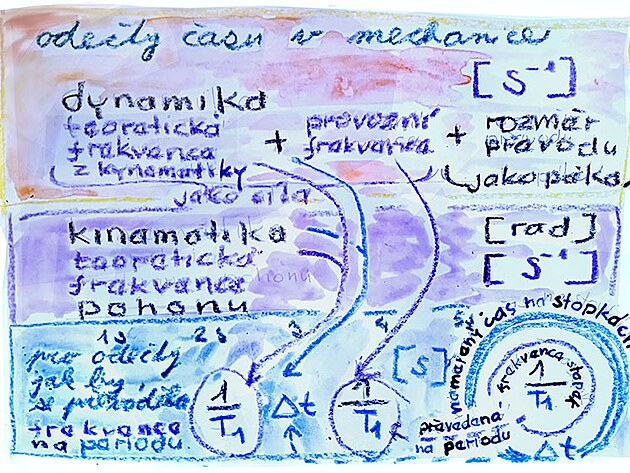
jednotky času (dynamika, kinematika - a reálné vjemy)

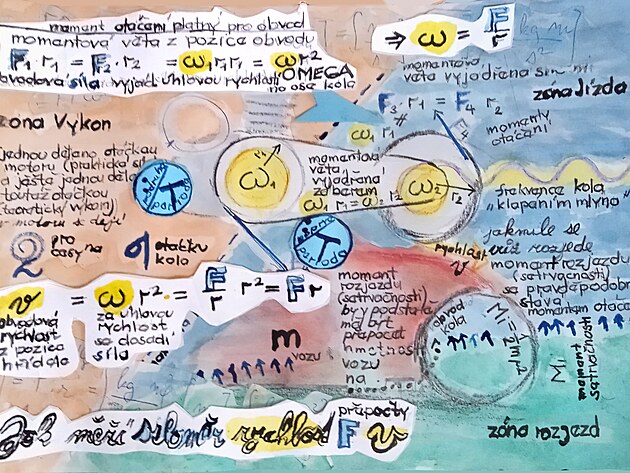
Veličiny které se zkoumají při výpočtu výsledné rotační rychlosti kola, nebo úhlové rychlosti (síly) - nejnázorněji pokud by se například kolo pohánělo zkušebně něčím jako pružinou siloměru - tedy veličiny v dynamice, jsou ty samé veličiny - jako zkoumané veličiny v kinematice  - tedy frekvence stopek a interval měření (vyjádřeno s větší přesností - zatímco frekvence stopek se započítává dvakrát - jednou pro vyjádření teoretické kinematiky pohonu - po druhé pro vyjádření síly pro pohon, tedy energie dodávané k otáčení - druhá zkoumaná veličina, tedy délka měření - interval měření se započítává jen jednou - teoreticky je ovšem přiřazen do kinematické části měřených veličin)

tedy znovu shrnuto - dvě zkoumané veličiny při měření otáček kola jsou 

- frekvence  f1 stopek - jedna vteřina (jedna inverzní vteřina jako kinematická veličina)

- a  naměřený čas DeltaT  (interval) na stopkách (veličina v reálném čase) 

frekvence  f1 stopek se v podstatě porovnává s naměřeným časem DeltaT  (intervalem) na stopkách 

frekvence "stopek"  f1 se ve výpočtech vyskytuje dvakrát - poprvé při výpočtu kinematické teoretické frekvence pohonu - a po druhé při přepočtu na úhlovou rychlost - tedy de fakto  provozní sílu pohonu - již veličinu která spadá do dynamiky 

naměřený čas DeltaT  (interval) na stopkách se vy výpočtech vyskytuje jen jednou - teoreticky jde o přepočet v kinematice (protože s při stanovení úhlové dráhy vzájemně KRÁTÍ  jednotky času- tedy inverzní sekundy na mínus prvou frekvence stopek (frekvence  f1)  a naměřený čas na stopkách čas DeltaT v sekundách. 

to co se děje uvnitř pohonu - jako by vydávalo jiné zvuky vně - třeba k posluchači zaznamenávající zvuky vozidla na nástupišti

frekvence pohonu - jak by se měnila v periodu zvuku pro posluchače vně

frekvence "stopek"  f1 se ve výpočtech převádí na perioduT1, tedy s čitatele do jmenovatele - také se při reálných vjemech (řekněme zvucích pohonu vnímaných na nástupišti) zvuky formují v jednotkách času - vteřinách a dalších - čili perioda v sekundách je vlastně frekvence v inverzních sekundách převedená do reálného času zaznamenávaného v sekundách jako periodické klapání pohonu - teoreticky i klapání mlýna

OBSAH

VUT Brno
Rozcestník VUT Brno

přepočty 

část1 JAK MĚŘÍ SILOMĚR SÍLU  - rychlost nebo síla ?(první část)
Rozcestník matematika 
Rozcestník mechanika pohybu - kinematika a dynamika, rozcestník převody

část 2 rozbor měření - veličiny a jednotky času (dynamika, kinematika - a reálné vjemy)(člen převodu č. 1 pastorek) / kinematika - jako nauka o pohybu - frekvence a úhlová dráha (a dále pak dynamika - jako  nauka o rychlosti a výkonu- o dynamice však až v dalších částech příspěvku)

část 3 (člen převodu č. 1 pastorek) / kinematika - jako nauka o pohybu - frekvence a úhlová dráha (a dále pak dynamika - jako  nauka o rychlosti a výkonu- o dynamice však až v dalších částech příspěvku)
3s / výpočet frekvence a obvodové rychlosti na otáčejícím se kole jen s výpomocí "stopek"
JAK MĚŘÍ SILOMĚR SÍLU  (druhá část)

3pokračování/ výpočet frekvence a obvodové rychlosti na otáčejícím se kole jen s výpomocí "stopek"
část 4 (člen převodu č. 2 - kolo pohonu) / dynamika 2 - rotační rychlost, úhlová rychlost, síla, moment síly a siloměr  - přepočty kinematicko dinamických veličin

část 5 přepočty hmotnosti a síly a kladkostroj

část 3 (člen převodu č. 1 pastorek) / kinematika - jako nauka o pohybu - frekvence a úhlová dráha (a dále pak dynamika - jako  nauka o rychlosti a výkonu- o dynamice však až v dalších částech příspěvku)

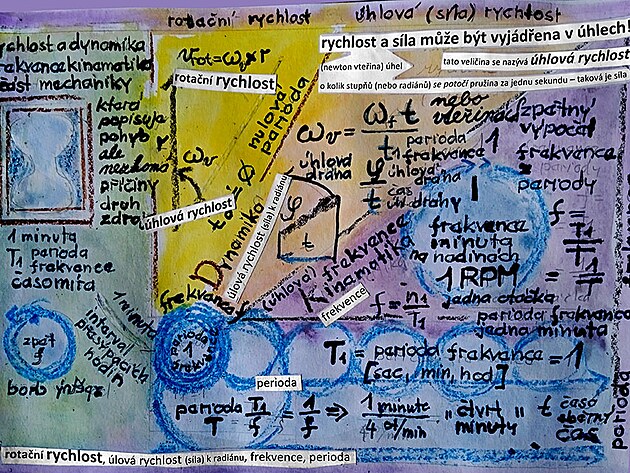
jaký je vlastně rozdíl mezi dvěma disciplínami mechaniky - kinematikou a dynamikou...

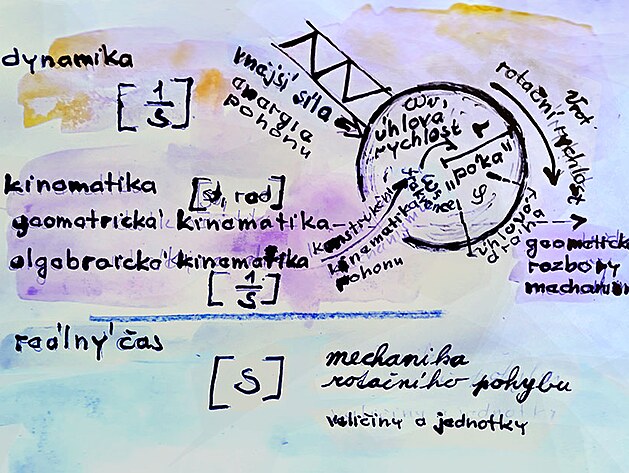
kinematika je nauka o pohybu mechanismu

- podstatná pro tento pohyb je sice konstrukční výkonost zkoumaného mechanismu  - v kinematice vyjádřena frekvencí - ovšem značná část kinematických rozborů se odehrává bez veličiny čas - tedy jde spíše o rozbory geometrických dějů mezi jednotlivými částmi mechanismu

kinematiku jakoby tvořily dvě (nebo 3) odlišné části

1a 2/ algerbraická kinematika, kinematika pro dynamiku s veličinou čas vyjádřenou frekvencí

3/ geometrická kinematika, kinematické rozbory zcela bez času jako východisko pro rozbory pohybu mezi jednotlivými částmi mechanismu - pokud by se geometrické rozbory převedly do algebry - tak by se mělo jednat o frekvenci přepočtenou na úhlovou dráhu - kde se jednotka času vlastně krátí mezi zkoumaným intervalem času Delta t a frekvencí měřidla  vyjádřenou periodou 1/T1

přepočtům času (frekvence i amplitudy) na bezrozměrnou veličinu "úhlová dráha PSÍ" je věnován příspěvek

Mechanika KFD - perioda, frekvence, obvodová rychlost /kinematika fotbalového míče /  proč rychlé vozy mají velká kola - Blog iDNES.cz 

další bádání nad disciplínou "kinematika" v části "

dynamika je nauka o výkonu a rychlostech - rovněž především mechanismů   

Frekvence, možná přesněji kinematická frekvence - je velmi  nenázorná veličina - bezrozměrná - stejná frekvence je v ose pohonu, stejný frekvence je na obvodu převodu - a navíc je vyjádřena v inverzních sekundách na mínus prvou - a dále se jedná o čistě teoretickou veličinu - která univerzalizuje různé druhy pohonu - jejich konstrukční rychlost a sílu - právě do kinematické veličiny frekvence.

Frekvencí se tedy zabývá kinematika - což je nauka - možno říci nauka o charakteru pohybu - ale nedává výsledek - výsledkem - tedy výslednou rychlostí, či výkonem se zabývá dynamika - což je nauka o rychlosti. Význam v dynamice má nejen výsledná rychlost - zde v případě zkoumání pohonu a jeho frekvence rychlost rotační - ale i přechodná veličina úhlová rychlost.  

Jak se tedy může měřit frekvence, potažmo úhlová dráha ( což je v podstatě také frekvence - ale nikoli v jednotkách času - ale otáčkách v úhlech). V kinematice má úhlová dráha možná ještě větší význam než kinematická frekvence - protože kinematické rozbory se snáze určují v úhlech - než v inverzních sekundách frekvence.

A úhlová dráha není jenom frekvence - ale už v podstatě síla - protože frekvence naznačuje právě sílu pohonu - z výsledné rotační rychlosti tvořené silou a páku z frekvence pohonu vyplývá vlastně síla..

OBSAH

VUT Brno
Rozcestník VUT Brno

přepočty 

část1 JAK MĚŘÍ SILOMĚR SÍLU  - rychlost nebo síla ?(první část)
Rozcestník matematika 
Rozcestník mechanika pohybu - kinematika a dynamika, rozcestník převody

část 2 rozbor měření - veličiny a jednotky času (dynamika, kinematika - a reálné vjemy)(člen převodu č. 1 pastorek) / kinematika - jako nauka o pohybu - frekvence a úhlová dráha (a dále pak dynamika - jako  nauka o rychlosti a výkonu- o dynamice však až v dalších částech příspěvku)

část 3 (člen převodu č. 1 pastorek) / kinematika - jako nauka o pohybu - frekvence a úhlová dráha (a dále pak dynamika - jako  nauka o rychlosti a výkonu- o dynamice však až v dalších částech příspěvku)
3s / výpočet frekvence a obvodové rychlosti na otáčejícím se kole jen s výpomocí "stopek"
JAK MĚŘÍ SILOMĚR SÍLU  (druhá část)

3pokračování/ výpočet frekvence a obvodové rychlosti na otáčejícím se kole jen s výpomocí "stopek"
část 4 (člen převodu č. 2 - kolo pohonu) / dynamika 2 - rotační rychlost, úhlová rychlost, síla, moment síly a siloměr  - přepočty kinematicko dinamických veličin

část 5 přepočty hmotnosti a síly a kladkostroj

3s/ výpočet frekvence a obvodové rychlosti na otáčejícím se kole jen s výpomocí "stopek"

malá anotace na úvod - porovnání dvou zdánlivě nesouměřitelných veličin (síla - přesněji moment síly) z nichž každá má jiná zdroj (síla hmotnost) - rychlost zase frekvenci pohybu - a obě tyto veličiny se setkávají na kolech vozidel - zatímco moment síly má maximum uprostřed kola - síla zase na obvodu - obě veličiny se však dají poměřovat - k čemuž složí zařízení zvané siloměr

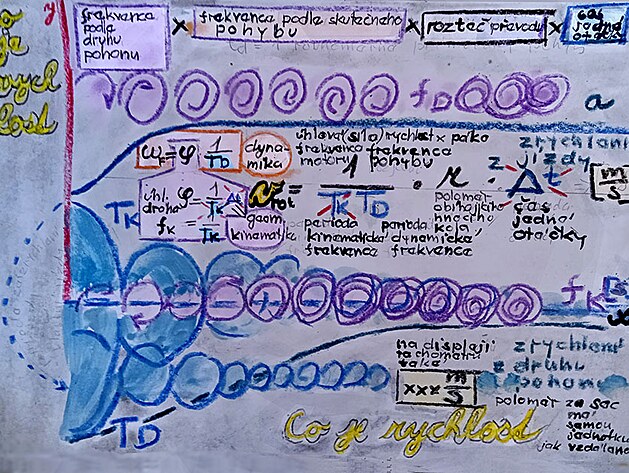
rotační rychlost jako součin kinematické frekvence mechanismu krát doba jedné otáčky krát úhlová rychlost mechanismu již v provozu krát rozteč převodu

(novelizace)

 

úhlová dráha a úhlová rychlost jako přechodové veličiny mezi kinematikou a dynamikou

(původní příspěvek)

Podstatou tohoto příspěvku by měly být přechodné veličiny - méně známé veličiny kinematiky a dynamiky -  jako jsou zde například úlová rychlost - či úhlová dráha - které by měly být něčím jako kloubem mezi různými disciplínami  - zde například dynamiky a kinematiky - a snad zjednodušovat výpočty, či přepočty mezi výslednými a vstupními veličinami, a tyto řekněme přechodné veličiny jsou také méně známé než výstupní veličiny jako třeba rychlost či frekvence - které se zobrazují třeba na tachometru - nebo otáčkoměru. Ostatně i tyto výstupní veličiny frekvence a rychlost jsou spíše známé než probádané. 

 Ale k přechodným veličinám, které figurují uprostřed výpočtů , jako zde zmíněná veličiny úlová rychlost  či úhlová dráha. Už nesourodá dvojice v názvech těchto veličin naznačuje, že tato dvojice k sobě nesourodých pojmů naznačuje že tato dvojice pojmů může být něčím jako poměrem, který směřuje k nějakému třetímu pojmu - který z těchto pojmů vyplývá. A protože rychlost tvoří síla a páka, tak veličina síla by právě měl být ten pojem - který se vstřebává za názvosloví jiných veličin během přepočtových rovnic - od vstupních údajů k výsledku. 

Zmíněné veličiny úlová rychlost  či úhlová dráha, by měly být právě osíle. A protože kinematika spíše zkoumá samotný pohyb a v dynamice jsou podstatné spíš výpočty rychlosti - už tyto poněkud nesourodé dvojice v názvech úlová rychlost  či úhlová dráha, by mohly spojovat dva rozdíly, by mohly být kloubem mezi disciplínami mechaniky - jako je kinematika a dynamika - a v případě veličiny úhlová dráhaby se mohlo jednat o kloub mezi algebraickou a geometrickou kinematikou. 

3pokračování/ výpočet frekvence a obvodové rychlosti na otáčejícím se kole jen s výpomocí "stopek"

FREKVENCE - nebo RYCHLOST se dají zjistit například OTÁČKOMĚREM - nebo jinými  přístroji, jenže v tomto případě zjištěná hodnota neozřejmí  nic o fyzikální podstatě veličiny

JAK SE VYPOČÍTÁ (NIKOLI JAK SE MĚŘÍ) FREKVENCE a ODVOZENÉ VELIČINY

například jak se vypočítá s měřením frekvence a rychlosti kola na bicyklu jen prostřednictvím stopek 

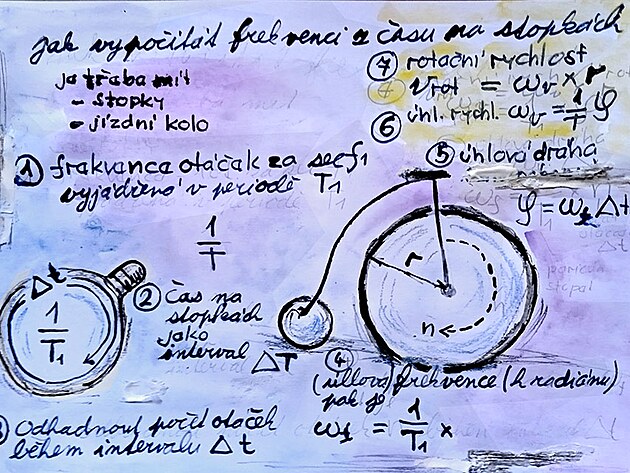
co je tedy potřeba mít

1/stopky 

a přepočíst interval jejich frekvence na vteřiny - tedy otáčky za vteřinu (f1) a tuto frekvenci ve výpočtech převést na frekvenci vyjádřenou periodou (1/T1)

2/ dále při měření otáček kola na stopkách odečíst na stopkách interval měření, tedy Deltat

otáčející se kolo - a během intervalu měření odpočítat - nebo alespoň odhadnout počet otáček kola -počet otáček n

3/ vyhodnocení a výpočet frekvence a obvodové rychlosti kola na základě časového intervalu Delta t - odečteného na stopkách

výchozí veličiny a výsledky

T1 perioda stopek v sekundách - tedy jedna otáčka převedená z minut na vteřiny

n ... zaznamenaný, nebo odhadnutý počet otáček kola

Delta t - zaznamenaný interval na stopkách, po který se měří otáčky kola

na základě jednoduchého měření lze zjistit

K - kinematické vlastnosti mechanizmu (zde třeba kola bicyklu) - tedy kinematiku pohonu kola, která odráží rozsah a průběh otáček - které lze zkoumaným pohonem dosáhnout

D - dynamické vlastnosti vnější sía otáčející kolem - tedy energie pohonu

podrobněji výsledky měření 

K - kinematické vlastnosti mechanizmu

frekvencef= (1/T) krátn 

D - dynamické vlastnosti například vnější síla otáčejícím kolem - například síla ze cyklistických šlapátek

obvodová rychlost  OMEGA v  = (1/T)krát n  krát  (1/T) krát Delta t 

slovy: otáčky stopek za vteřinu x zaznamenaný - či odhadnutý počet otáček x otáčky stopek za vteřinu x zaznamenaný na stopkách

a výsledná obvodová síla kola

rotační rychlost  v  = úhlová rychlost OMEGA  (rýchlostnost na ose)  krát poloměr kolar

rotační rychlost  v  = (1/To) krát n  krát  (1/To) krát Delta t krát poloměr r

rotační rychlost  v  = počáteční frekvencef krát n  krát   počáteční frekvence f krát rozdíl ve zkoumané periodě T1 - T2  krát poloměr r

rotační rychlost  v  = počáteční frekvence f krát n  krát  (1/To) krát výsledná perioda  T2  krát poloměr r

z výsledku  rotační rychlost  v  = (1/T) krát n  krát  (1/T) krát Delta t krát poloměr r by mělo vyplynout, že

rotační rychlost  v  = úhlová rychlost OMEGA  (rýchlostnost na ose) v krát  poloměr kolar

rotační rychlost  v  = SÍLA (z tlaku)  krát  plochaS (poloměrr na druhou) lomeno PÁKA (poloměrr)

dále z výpočtu vyplývá, že jediným NEPŘÍMÝM měřícím prvkem - tedy otáčkou stopek v sekundách

lze popsat

jednak kinematiku mechanismu

 a za druhé - vnější sílu působící na kolo - třeba přes šlapátka - tedy veličinu z oboru  dynamika

rozbor veličin u pružinového siloměru by měl poskytnout jistý nástin rozčlenění veličin - nicméně k této části příspěvku se nevztahuje měření siloměrem - zde jen nastíněn výpočet frekvence a rychlosti zaznamenáním času na stopkách

znovu zde připomenuto 

veličiny síla F a rychlost v mají obdobnou podstatu - pře přepočtech v kinematice - dynamice - rychlost vychází z rotace - a síla zase z tlaku vně - jinak obě veličiny se v mechanice často  vyskytují dohromady - a jejich násobkem je výkon P

OBSAH

VUT Brno
Rozcestník VUT Brno

přepočty 

část1 JAK MĚŘÍ SILOMĚR SÍLU  - rychlost nebo síla ?(první část)
Rozcestník matematika 
Rozcestník mechanika pohybu - kinematika a dynamika, rozcestník převody

část 2 rozbor měření - veličiny a jednotky času (dynamika, kinematika - a reálné vjemy)(člen převodu č. 1 pastorek) / kinematika - jako nauka o pohybu - frekvence a úhlová dráha (a dále pak dynamika - jako  nauka o rychlosti a výkonu- o dynamice však až v dalších částech příspěvku)

část 3 (člen převodu č. 1 pastorek) / kinematika - jako nauka o pohybu - frekvence a úhlová dráha (a dále pak dynamika - jako  nauka o rychlosti a výkonu- o dynamice však až v dalších částech příspěvku)
3s / výpočet frekvence a obvodové rychlosti na otáčejícím se kole jen s výpomocí "stopek"
JAK MĚŘÍ SILOMĚR SÍLU  (druhá část)

3pokračování/ výpočet frekvence a obvodové rychlosti na otáčejícím se kole jen s výpomocí "stopek"
část 4 (člen převodu č. 2 - kolo pohonu) / dynamika 2 - rotační rychlost, úhlová rychlost, síla, moment síly a siloměr  - přepočty kinematicko dinamických veličin

část 5 přepočty hmotnosti a síly a kladkostroj

část 4 (člen převodu č. 2 - kolo pohonu) / dynamika 2 - rotační rychlost, úhlová rychlost, síla, moment síly a siloměr  - přepočty kinematicko dinamických veličin

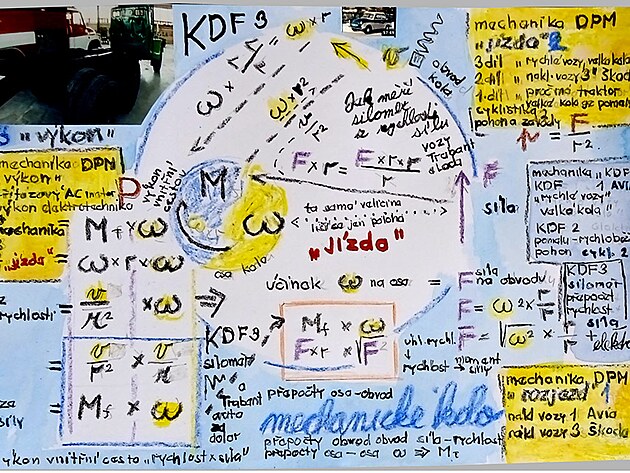
převodem z pastorku na druhé kolo pohonu se přepočte frekvence a úhlové pootočení na tzv. úhlovou rychlost - což je veličina v ose druhého kola - tedy kola pohonu - kterou se přenáší otáčky z výstupní kolo vozidla - úhlová rychlost ovšem má stejný význam jako veličinasíla - tedy přenáší pohyb dál - úhlová rychlost by měla být podrobněji až v další části - zde podrobněji k veličině síla  která má sice stejný účinek - ale jiné působiště a velikost a také lineární průběh

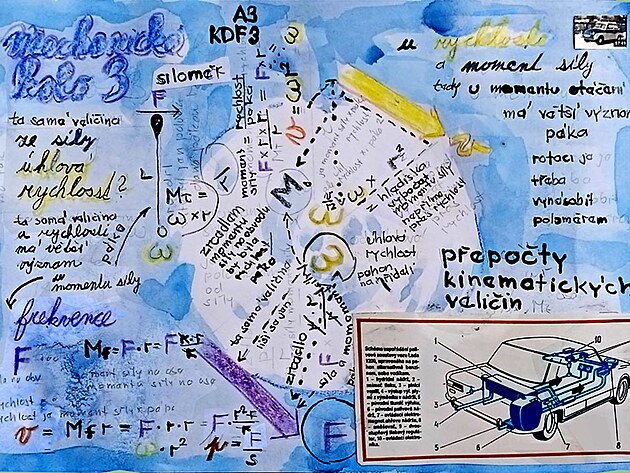
Pružinový siloměr je určený k měření síly prostřednictvím úhlu pootočení a měří ´v podstatě frekvenci - nebo přesněji - úhlovou rychlost - což je již veličina dynamiky - a to z hlediska algebraické posloupnosti kinematická frekvence přepočtená přes úhlovou dráhu (znovu připomenuto rovněž kinematická veličina - frekvence vyjádřená nikoli v čase, ale úhlové míře) vynásobená podruhé frekvencí stopek na zjišťovanou veličinu - kterou je úhlová rychlost (úhlová síla) .  Kinematická úhlová dráha - tedy celkový úhel otáček - je již téměř to co se měří na siloměru - jen matematickým přepočtem - vynásobením úhlové dráhy jednou inverzní sekundou frekvence hodin, tedy tímto dalším přepočtem již vyplývá výsledná veličina zjišťovaná na siloměru - .tedy - úhlová rychlost.

A - úhlová rychlost  v případě měření na siloměru je vlastně síla - vyjádřená v inverzních sekundách na mínus prvou. Siloměr vlastně měří jednak úhel potočení měřidla  - jednak  se výsledkem dá vyjádřit síla působící na pružinu siloměru - jednak lze - pokud se interval měřeníDelta t zaznamená na stopkách - lze  se výsledek měření přepočíst na frekvenci, potažmo rychlost - přesněji úhlovou rychlost.  

Úhlová rychlost by také klidně, nebo dokonce výstižněji nazvána jako úhlová síla - přesto, že  jednotkou úhlové rychlosti  jsou inverzní, či "žravé" sekundy - sekundy na mínus prvou. Úhlová rychlost - navzdory poněkud nezřetelného názvu zase rychlost příliš nevyjadřuje - a pokud rychlost nějak vyjadřuje - vyjadřuje je jen nepřímo - či spíš inverzně - jak ostatně naznačují použité jednotky pro úhlovou rychlost - výše zmíněné inverzní sekundy na mínus prvou. 

. 

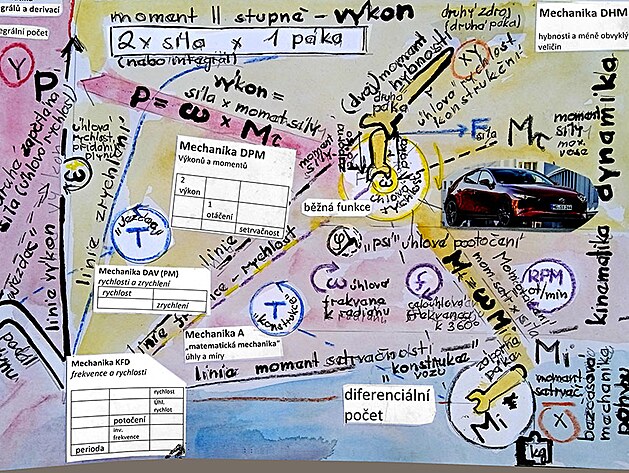
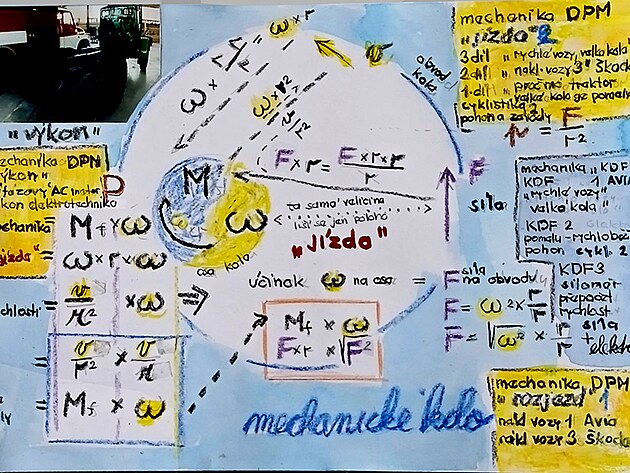
dynamika

úhlová rychlost (v podstatě)  síla od které se liší jenom  působištěm (úhlová rychlost má působiště na ose, síla na obvodu)

rotační rychlost (má působiště na obvodu)

ale není ekvivalentem veličiny úhlová rychlost na ose - jak by napovídal název, ale veličiny moment otáčení, neboli síly

kinematika: kinematická frekvence (něco jako žravý čas)

běžné vjemy: perioda T

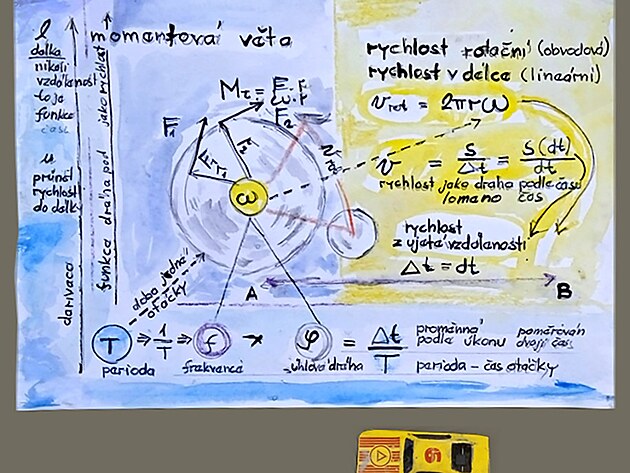
novelizace: rotační rychlost je úhlová rychlost krát poloměr na druhou

v nákresu nesprávně uvedeno...

dynamika: Tnula - nulový čas-  veličina čas vykrácena ve výpočtech 

(i dráha obsahuje vlastně veličinu čas - na rozdíl od poloměru - který je zcela bezčasový)

chyba v nákresu výše rotační rychlost je vlastně vektorový součin úhlové rychlosti (síly) a poloměru kružnice - neboli ramene

rotační rychlost vychází z momentu síly a zde platí vzorec - moment síly je úhlová rychlost OMEGA krát poloměr - i když obě veličiny mají "sídlo" na ose kola

platí tedy přepočet rotační rychlost na obvodu je moment síly krát poloměr, tedy celý rychlost pro rotační rychlost ba zněl 

úhlová rychlost poprvé vynásobena poloměrem na moment síly - po druhé na rotační, či obvodovou rychlost

úhlová rychlost je podíl úhlové dráhy (která zahrnuje veličinu čas - neboť tato je násobkem kinematické frekvence která obsahuje inverzní - neboli- lomeno (či děleno) časem periody T1 - tedy periodou hodin

kinematika - kinematická frekvence (úhlová, k celému úhlu 360, otáčky za minutu RPM) 

kinematická frekvence je něco jako žravý čas - na roz

část 5 převody, přepočty síla – hmotnost a kladkostroj

Matematika ve strojírenství - rozcestník převody a jeřáby

Matematická mechanika  A0/ KFD 0 jak měří siloměr přes rychlost sílu / výpočty přes stopky - převody 1 (tento příspěvek)

Převody mechanické (kolo a pastorek) a elektrické (trafa) - vozy Mercedes a vojenství - Blog iDNES.cz

Návštěva staré tiskárny - části strojů a mechanismy - Blog iDNES.cz

Mechanika JB /DPMW přístavní jeřáb - jak se připojit k internetu 4 (přirovnání k přístavu) - Blog iDNES.cz mechanické výpočty pro jeřáb

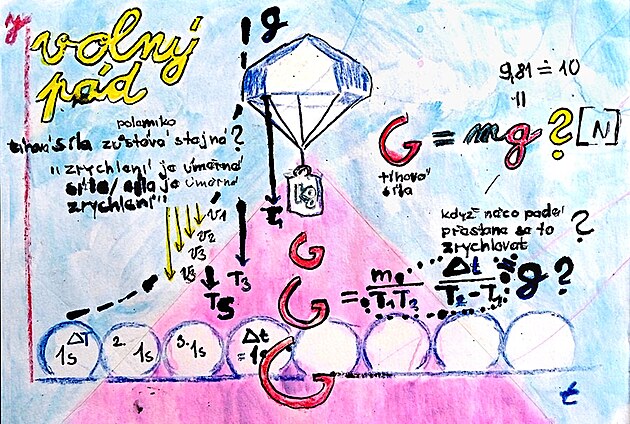
mění se při gravitačním pohybu dolů jen rychlost, nebo i tíha?

První problém. Síla, tíhová síla, tíha v newtonech jako proměnná na jedné straně a hmotnost v kilogramech na druhé straně jsou si veličiny podobné, příbuzné – až zaměnitelné – přesto jejich přepočet vůbec není jednoznačný – nejčastěji se používá přepočet vycházející ze zrychlení. To je jeden problém.

Druhý problém je – při pohybu na základě hmotnosti, potažmo tíhy směrem dolů – od volného pádu po pohyb směrem dolů po nakloněné rovině – že narůstá rychlost – to je fakt – ale narůstá i tíhová síla? To je otázka která není jednoznačně vyřešena. Podle některých názorů se mění jen rychlost jako následek – a síla jako příčina je tatáž, jako byla na začátku sestupu – podle některých náznaků narůstá i tíha. Ovšem asi je výhodnější brát sílu jako konstantní – stejnou jako na počátku – a veličinou která se například při pádu mění – by pak byla jen rychlost.

volný pád

nakloněná rovina – svážnice – pozemní lanovka

svážnice Josefová v Jeseníkách

přepočet hmotnost – síla, tíhová síla, tíha

Tíha neboli síla je udávána jako přibližně desetinásobek (9.81 krát) hmotnosti – měřeno na určité jednoznačné zeměpisné poloze. Jenomže například při odlišné poloze – a především výšce od země by se skutečná tíha mohla teoreticky zásadně lišit – nicméně jako úzus pro přepočet hmotnosti na tíhu bere výše zmíněný přepočet.

Pokud by měl být přepočet hmotnost nějak definován – tak by se zřejmě mělo jednat o přepóčet hmotnost krát čas zkoumané doby.

Ovšem technicky metodiky přepočtu hmotnosti na sílu – tedy kilogramů na newtony nejsou tak trivální jako vynásobit hmotnost dobou zkoumaného času – identifikovány byly vlastně dvě odlišné metotudy – 1/ přepočet hmotnosti na tíhu (tíhovou sílu) na základě zrychlení a 2/ přepočet hmotnosti na sílu na základě momentu setrvačnosti, který vychází z hmotnosti vozu – přesněji z hmotnosti vozu přenesené na kolo vozu. A ještě jedna zajímavost – 3/ pokud by se postupovalo opačně – že by se zkoušela přepočítat síla či tíha v newtonech na hmotnost – pak by vznikla veličina impuls síly „I“. Impuls síly má jednotku newtonsekunda – a jedná se vlastně o sílu vynásobenou zkoumanou dobou na veličinu která se nápadně podobá hmotnosti – impuls síly „bezčasová síla“.

1/ přepočet hmotnosti na tíhu na základě zrychlení

2/ přepočet hmotnosti na sílu na základě momentu setrvačnosti

3/ impuls síly (opačný postup) – síla vynásobená zkoumanou dobou úkonu ze „zóny jednou děleno časem“ do zóny „bezčasí“ – čímž vzniká veličina nápadně se podobající bezčasové hmotnosti – což je veličina impus síly v newtonsekundách.

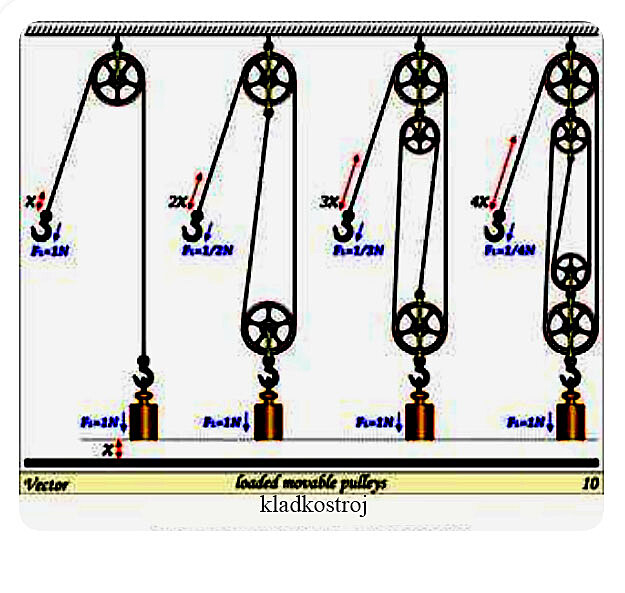
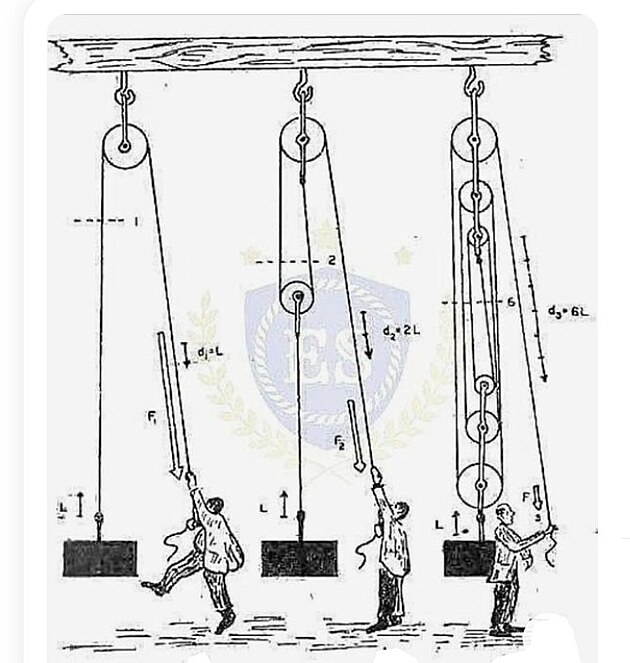
kladkostroj

různé varianty kladkostrojů

OBSAH

VUT Brno
Rozcestník VUT Brno

přepočty 

část1 JAK MĚŘÍ SILOMĚR SÍLU  - rychlost nebo síla ?(první část)
Rozcestník matematika 
Rozcestník mechanika pohybu - kinematika a dynamika

část 2 rozbor měření - veličiny a jednotky času (dynamika, kinematika - a reálné vjemy)(člen převodu č. 1 pastorek) / kinematika - jako nauka o pohybu - frekvence a úhlová dráha (a dále pak dynamika - jako  nauka o rychlosti a výkonu- o dynamice však až v dalších částech příspěvku)

část 3 (člen převodu č. 1 pastorek) / kinematika - jako nauka o pohybu - frekvence a úhlová dráha (a dále pak dynamika - jako  nauka o rychlosti a výkonu- o dynamice však až v dalších částech příspěvku)
3s / výpočet frekvence a obvodové rychlosti na otáčejícím se kole jen s výpomocí "stopek"
JAK MĚŘÍ SILOMĚR SÍLU  (druhá část)

3pokračování/ výpočet frekvence a obvodové rychlosti na otáčejícím se kole jen s výpomocí "stopek"
část 4 (člen převodu č. 2 - kolo pohonu) / dynamika 2 - rotační rychlost, úhlová rychlost, síla, moment síly a siloměr  - přepočty kinematicko dinamických veličin

část 5 přepočty hmotnost a síla a kladkostroj