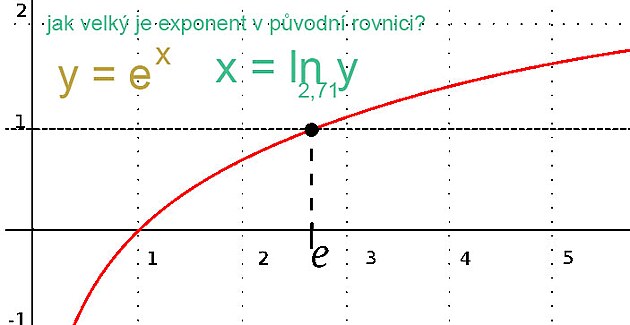A11V Rovnice, funkce, derivace, integrály, logaritmy
OBSAH
část 1
ROVNICE A FUNKCE
část 2
INTEGRÁLY A DERIVACE
část 3
LOGARITMY a LOGARITMICKÉ ROVNICE
část 4
EULEROVA KONSTANTA
část 5
ROVNICE A FUNKCE - a konkrétní veličiny v mechanice pohybu - rychlost, zrychlení, síla, výkon
dva úvodní příspěvky pro matematiku
Matematická mechanika A0/ KFD 0 jak měří siloměr přes rychlost sílu / výpočty přes stopky - Blog iDNES.cz frekvence, úhlová dráha, úhlová rychlost, moment otáčení, síla, rychlost obvodová a lineární - kinematika, dynamika, mechanika pohybu
Mechanika A/ KFD : kinematika (frekvence), dynamika (úhlová a obvodová rychlost) - Škoda - Blog iDNES.cz frekvence, úhlová dráha, úhlová rychlost, moment otáčení, síla, rychlost obvodová a lineární - kinematika, dynamika, mechanika pohybu ˇ+ doplňkové výpočty - Ludolfovo číslo, Eulerovo číslo, přepočty druhů frekvence a úhlů
vnitřní matematika – matematika přepočtů
vnější matematika – matematické funkce (i pro jiné obory)
Jaký je vlastně rozdíl mezi levou a pravou rovnice a rovnicí, funkcí a veličinou - a dále pak integrálem a derivací - na to by se měl pokusit odpovědět tento příspěvek...
OBSAH
část 1
ROVNICE A FUNKCE
část 2
INTEGRÁLY A DERIVACE
část 3
LOGARITMY a LOGARITMICKÉ ROVNICE
část 4
EULEROVA KONSTANTA
vlastní příspěvek
část 1 rozdíl mezi rovnicí a funkcí - průběh funkce
"část 1" příspěvku je společná s příspěvkem Nádraží a vlak - rychlost a zrychlení - mechanika integrálních a diferenciálních počtů AV - Blog iDNES.cz
rovnice sice není přímo funkce, ale v mnoha případech rovnice a funkce může být totéž
nejprve rovnice - ovšem s levo - pravým dělením podle stran již jako funkce
Co je to vlastně vyjadřuje rovnice... Na vzdory rovnítka uprostřed neznamená, že levá a pravá strana rovnice vyjadřuje totéž.
LEVÁ STRANA ROVNICE - souhrnná neznámá "Y" (funkce, zjišťovaný pochod) - PRAVÁ STRANA ROVNICE spíš prostředek výpočtu,(zkoumaná veličina, konkrétní výsledek).- výkonná neznámá "x", případně "z"
LEVÁ STRANA ROVNICE (rychlost) - PRAVÁ STRANA ROVNICE spíš prostředek výpočtu, (zkoumaná veličina - dráha, funkce času).
druhy rovnic a funkcí
kvadratická rovnice - s neznámou - což je zpravidla x na druhou
funkce s x na druhou - teoreticky by se mělo jednat o kvadratickou funkci (toto označení se ale příliš nepoužívá) - pro tuto funkci se zde v příspěvcích používá i nepřesně označení exponenciální funkce
lineární rovnice s jednou neznámou a to na prvou
exponenciální rovnice - s neznámou v exponentu
logaritmická rovnice - teoreticky by byla příbuzná s exponenciální rovnicí - převrácená exponenciální rovnice
goniometrická rovnice - která zahrnuje funkce sinus a cosinus
Přehled rovnic a funkcí včetně integrálů a derivací...
Jaký je vlastně rozdíl mezi levou a pravou rovnice a rovnicí, funkcí a veličinou?
Jako základní matematická funkce může být považována lineární funkce.
Zde uveden příklad y = 2x - 6
přičemž y může být označena jako řídící neznámý, x jako výkonná neznámá
Typickým příkladem lineární funkce může být vzorec pro rychlost...
Obecně známý vzorec pro rychlost je sice dráha lomeno čas - ale zde uveden vzorec
rychlost "v" = OMEGA (tzv. úhlová rychlost na ose hřídele) x r na druhou (r = poloměr kola)
ostatně OMEGA (úhlová rychlost lze rozčlenit na veličiny frekvence a úhlová dráha PSÍ) - a při vynásobení poloměrem kola by z úhlové dráhy vznikla běžná dráha, kterou například urazí vozidlo ...
přímo veličinou rychlost se ale podrobněji zabývají jiné příspěvky - rychlostí konkrétně zejména příspěvek Mechanika KFD 1 DAV - frekvence, rychlost, zrychlení / proč rychlé vozy mají velká kola - Blog iDNES.cz
Přiřazováním konkrétních funkcí z mechaniky pohybu (rychlost, zrychlení, síla, výkon) by se měla věnovat pátá část tohoto příspěvku.
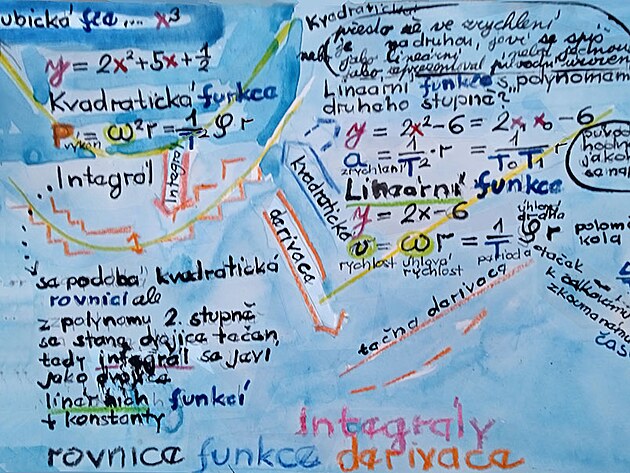
Podle přirozené posloupnosti by nad lineární rovnicí - či funkcí měla být kvadratická funkce (s výkonnou neznámo x na druhou, a pak například kubická rovnice s výkonnou neznámou x na třetí)
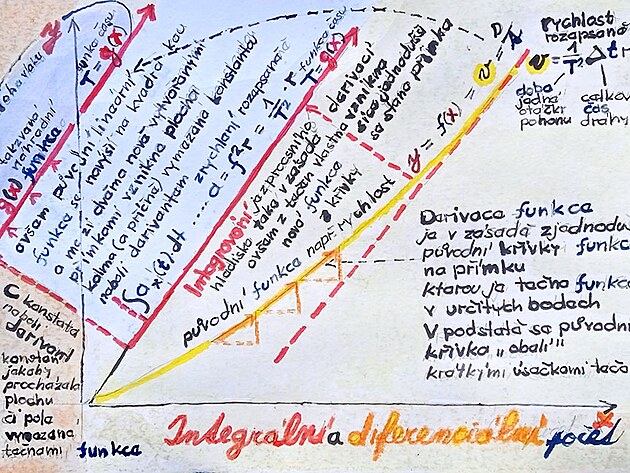
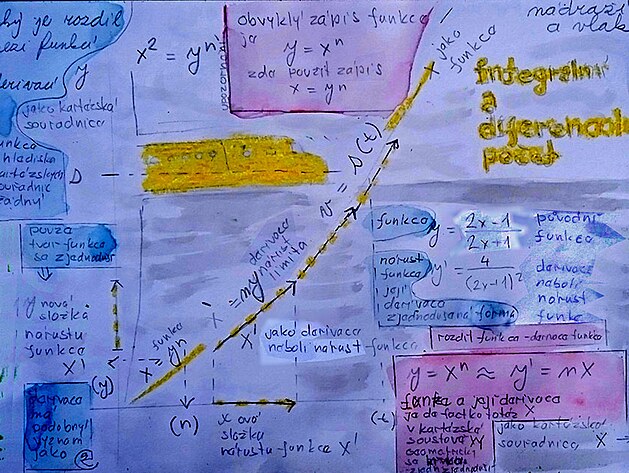
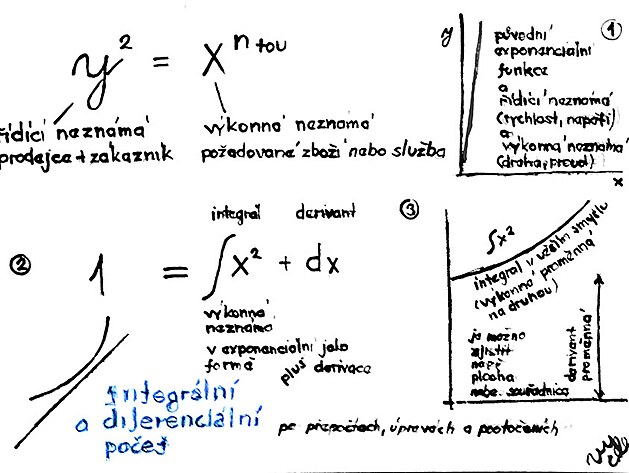
Vcelku zajímavou záležitostí jsou integrály a derivace - které vychází z kvadratické rovnice (tedy s výkonnou neznámou x na druhou) - ale tuto kvadratickou funkci zjednodušují tak - že vlatně původní křivku "obalí" prostřednictvím tečen k této křivce - neboť jak známo - lineární funkce - přímka - lze spočítat podstatně snáze než křivka. Stejnou metodiku - tedy nahrazení křivky přímkami se používá jak u derivování - tak integrování - nicméně původní křivce se více podobá asi derivace. Integrál se sice původní kvadratické funkci s "x na druhou" podobá alespoň v tom smyslu - že exponent se sice sníží - ale tečny vzniknou dvě. Součástí zápisu integrálu (zkratka pro integrál trochu připomíná nedotaženou osmičku) - tedy součástí zápisu integrálu je rovněž konstanta - někdy nazývaná jako derivant - a tato konstantana vlastně vytváří rozteč mezi tečnami - nebo jinak - boční stranu obdélníku - a tak v případě integrálu podél původní křivky vzniknou jakási pole - která původní křivku obalují - čímž se liší integrál od derivace i graficky. Pole z integrálů kolem původní křivky můžou mít různý význam - ale jeden z podstatných významů - že díky "polím integrálů" - lze například určovat poloha vlaku - přiblžně (a možná nepříliš přesně tak) - že jsou k jednotlivým stranám přiřazeny zeměpisné souřadnice - a derivant - či konstanta integrálu jakoby procházela pole integrálu z jedné strany na druhou - a tím se určovala například výše zmíněná poloha vlaku.
Zmíněny byly rovnice - kde se výkonná neznámá - tedy x nachází v základě rovnice - a tyto rovnice - či funkce jsou řešitelné obvyklými matematickými postupu - tedy například převáděním z jedné strany na druhou - krácením čitatele a jmenovatele - a tak dále...
Je však řada dalších rovnic - kde se výkonná neznámá - tedy x nachází jinde než v základu - například v exponentu - sínu, cosínu - případně nějakém jiném matematickém nástroji - a tyto rovnice či funkce jsou běžnými matematickými postupy - na principu kupeckých počtů - nesnadno řešitelné - ale tyto funkce lze řešit například prostřednictvím logaritmování - nebo logaritmických rovnic - což je něco jako doplňková - jednodušší rovnice - například pro neznámou x v exponentu exponenciální rovnice.
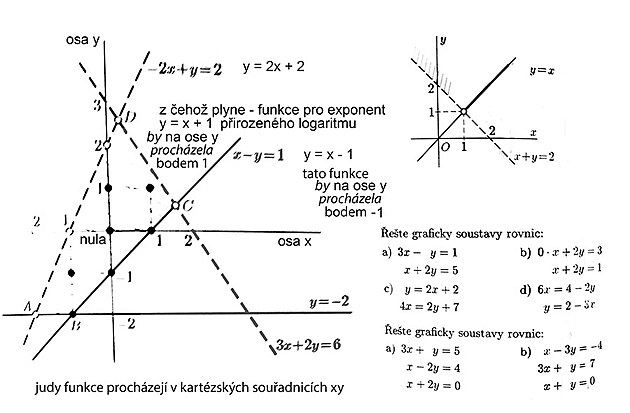
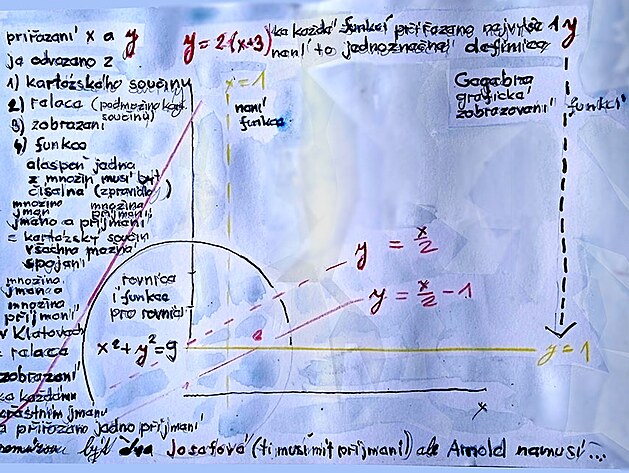
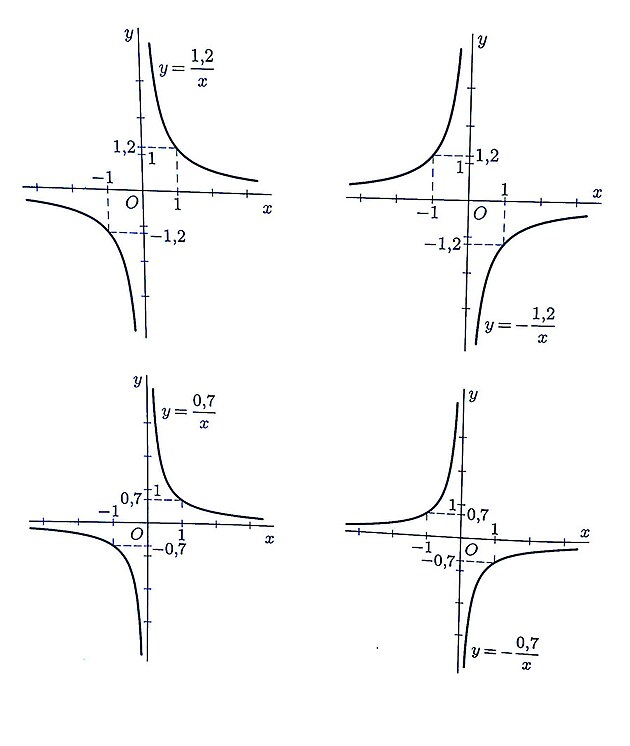
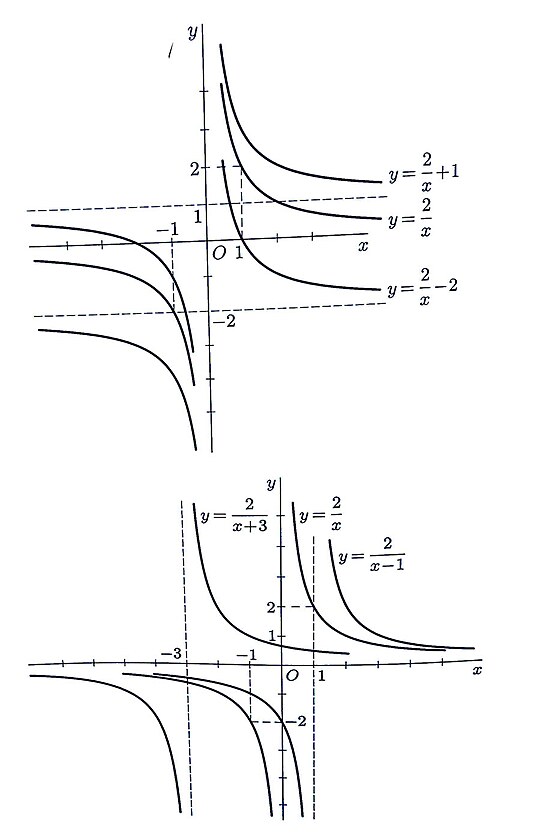
Kudy funkce procházejí v kartézských souřadnicích XY?
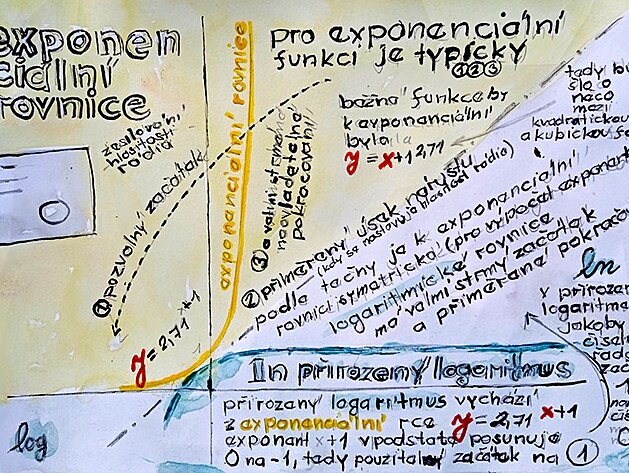
Algebraický zápis rovnice či funkce zároveň znamená určitou pozici v grafu XY - tedy polohu kudy zkoumaná funkce vlastně v souřadnicích prochází ...y = 1 značí, že funkce na ose prochází na stupnici číslicí 1y =x značí, že y se rovná x - tedy pokud je y nula je i x nula - funkce tedy vychází ze začátku - prochází osou y přes bod 0 - budu jedna na stupnici y odpovídá tedy bod 1 na stupnici x - tato funkce tedy stoupá přímouúměrně - tedy pod úhlem 45 stupňůy = x + 1 znamená - že výše uvedená funkce v náklonu 45 stupňů jakoby no ose y byla posunutá o jeden stupeň výše - do bodu 1, což znamená, že na ose x by procházela bodem -1 (nebo by bylo možno také brát - že tato funkce má začátek na stupnici x v bodě - 1 (ostatně uvedená rovnice je vlastně funkcí pro exponent přirozeného logaritmu...
na obrázku níže zobrazeny
žlutě: rovnice x = 1, která by stoupala strmě podél osy y, a pak funkce y = 1, jejíž průběh by byl podél osy x
červeně: funkce y = x/2 a funkce y = x/2 - 1 obě funkce směřují v úhlu 45st. mezi osami a druhá zmíněná funkce je o jednotku na stupnici posunutá
dále je zde uvedena kružnice - která je definována vzorcem x na druhou + y na druhou = 9
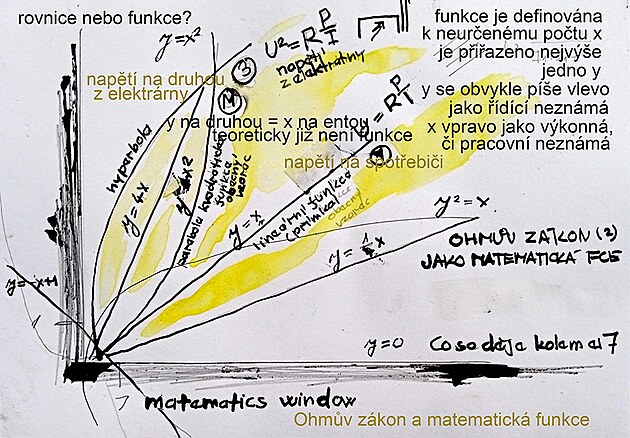
Funkce a příbuzné matematické záležitosti mohou mít jednak číselný (matematický) zápis - dále jdou zobrazit graficky - a rovněž zpravidla mají nějaký reálný význam - mohou popisovat průběh elektrotechnických veličin - veličin v mechanice - jako například průběh rychlosti - dále mohou popisovat úplně běžné záležitosti - různé přiřazování souvisejících veličin různých druhů...
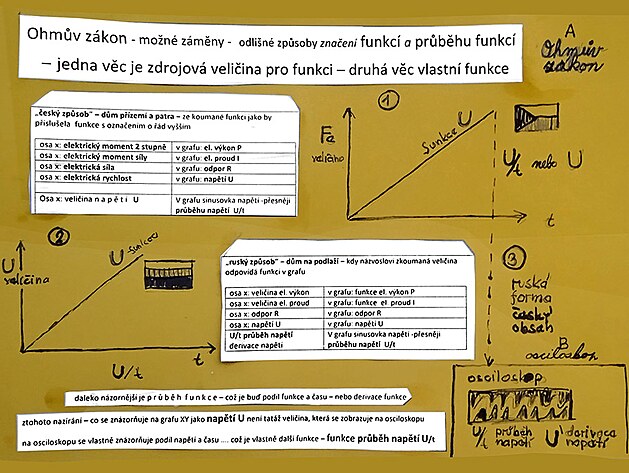
Konkrétní funkcí by třeba měl být i Ohmův zákon a to ve dvou variantách – pro spotřebič zapojený do zásuvky s napětím na prvou – což by odpovídalo matematické funkci y = x na entou – a průběh by byla přímka – nebo Ohmův zákon s napětím na druhou u elektrárny(s kohabitací výroba – spotřeba)- což by odpovídalo matematické funkci y na druhou = x na entou a průběh by byla hyperbola (je však na místě dodat, že z hlediska definice vlastně v „pravé“ funkci by „y“ mělo být pouze na prvou).
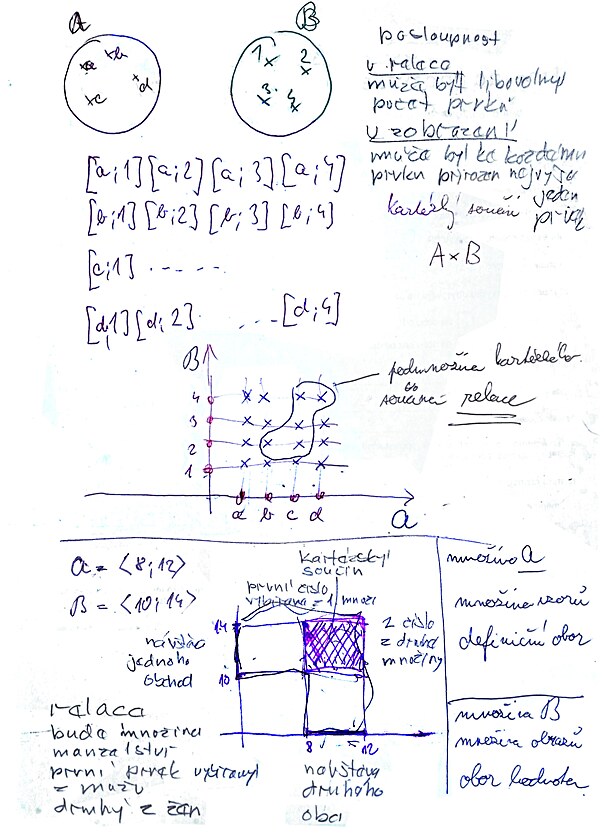
Kromě funkce se v matematice vyskytuje řada souvisejících záležitostí (viz tabuka níže), které mezi sebou souvisí a vytváří různé podmnožiny...
| relace | |
|---|---|
| /funkce |
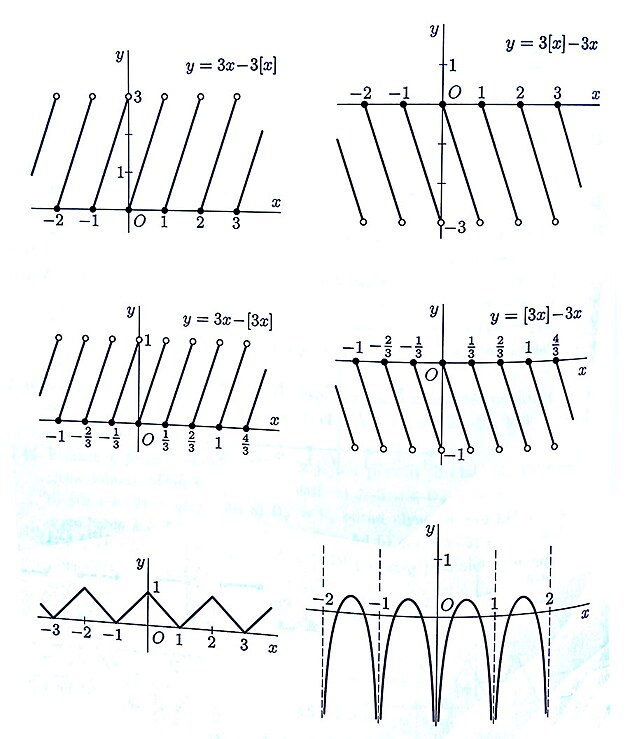
průběh funkcí
průběhy funkcí
druhy rovnic a funkcí a jejich průběh
lineární rovnice s jednou neznámou a to na prvou
kvadratická rovnice - s neznámou - což je zpravidla x na druhou
funkce s x na druhou - teoreticky by se mělo jednat o kvadratickou funkci (toto označení se ale příliš nepoužívá) - pro tuto funkci se zde v příspěvcích používá i nepřesně označení exponenciální funkce
exponenciální rovnice - s neznámou v exponentu
logaritmická rovnice - teoreticky by byla příbuzná s exponenciální rovnicí
goniometrická rovnice - která zahrnuje funkce sinus a cosinus
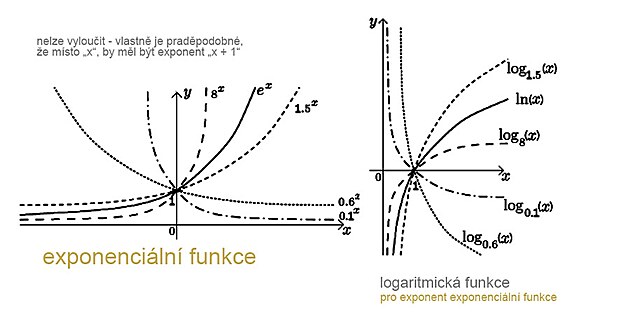
zajímavá věc - exponenciální a kvadratická funkce - přesněji jich grafický průběh - se poměrně podobají
kvadratická rovnice
y = x na druhou - což je výchozí rovnice pro funkci s kvadratickým členem - kvadratická rovnice obvykle ovšem obsahuje celkem tři členy...
malé pojednání o funkcích a veličinách
třeba už z názvosloví při značení funkcí mohou vznikat jisté nejasnosti
něco jiného je zdrojová veličina na ose y - a něco jiného je zjišťovaná funkce v grafu
Co je to vlastně vyjadřuje rovnice... Na vzdory rovnítka uprostřed neznamená, že levá a pravá strana rovnice vyjadřuje totéž.
LEVÁ STRANA ROVNICE - souhrnná neznámá "Y" (funkce, zjišťovaný pochod) - PRAVÁ STRANA ROVNICE spíš prostředek výpočtu,(zkoumaná veličina, konkrétní výsledek).- výkonná neznámá "x", případně "z"
LEVÁ STRANA ROVNICE (rychlost) - PRAVÁ STRANA ROVNICE spíš prostředek výpočtu, (zkoumaná veličina - dráha, funkce času).
poměrně důležitý pojmem je také
LICHÁ a SUDÁ funkce
pojmy LICHÁ (neúplná funkce - pouze s y) a SUDÁ funkce (plnohodnotná funkce - s y i x)
poměrně připomínají zde pracovně, či studijně zavedené pojmy
NEPRAVÉ DĚLENÍ (něco jako poměr mezi pruhy na vlajce, poměřování )
Veličina čas zde ČAS jako NEPRAVÝ DĚLITEL - KVALITIFIKÁTOR (matematická operace dělení zde ve smyslu ZMĚNA - podobající se chemickým reakcím při vytváření nových látek) .
PRAVÉ DĚLENÍ (něco jako porcování dortu)
(DVA druhy operandů ČASu při přepočtech mezi odlišnými druhy fyzikálních MOMENTů)
odkaz na původní příspěvek kde je zkoumáno "pravé a nepravé" dělení - a dva časy ve výpočtech -- jeden při ose y, druhý při ose X....
...dále již pokračování předchozích úvah o funkcích a rovnicích ....
ostatně z důvodů dvou různých
Y = X na n ou
v případě rychlosti
rychlost = dráha (jako funkce času) / lomeno čas
v grafu kartézských souřadnic je funkce poněkud jinak než v rovnici - pokud by se i rovnice zobrazila graficky - viz další část
rychlost (probíhá v meziose xy) =dráha (jako funkce času) - se zase odečítá na ose Y LOMENO čas(se zase odečítá na ose X
možná ještě názornější by posun v označení, případně názvosloví více vyjadřující podstatu veličiny by byl u veličiny rychlost
možná by bylo názornější, když by veličina měla stejné značení jako funkce
(na obrázku níže místo rychlosti elektrické napětí)
podle zde pracovně zavedeného ruského názvosloví, kdy se domy číslují na podlaží bez přízemí, by název pro rychlost mohl znít
"ruský způsob značení" - kdy se domy nečíslují na patra - ale podlaží a číslování vlastně začíná prvním podlažím
tedy veličině napětí U (zobrazované na ose y) odpovídá funkce napětí U (kolem meziosy xy)
jiný způsob značení by byl
"český způsob značení" - kdy číslování začíná přízemím a teprve další podlaží se nazývá první patro
tedy veličině elektrický výkon P (na ose Y) odpovídá funkce napětí U (kolem mezioy XY)
k obrázku výše "český a ruský způsob značení jisté vysvětlení" - v případě "českého" značení by na ose Y měl být výkon (U=RP) neboli napětí jako funkce výkonu, v případě tzv "ruského" značené (U=U)
shrnuto
exponenciální funkce nebo integrál : Y na druhou = X na entou
funkce : Y = X na entou
derivace.Ys apostrofem = n(tedy nárust funkce - neboli přímka)
z jednotlivých krátkých úseků "nárustů" funkce - se dá ovšem poskládat původní funkce (přesněji obrazec funkce, napodobenina funkce - křivka která se zobrazuje vlastně na osciloskopu)
OBSAH
část 1
ROVNICE A FUNKCE
část 2
INTEGRÁLY A DERIVACE
část 3
LOGARITMY a LOGARITMICKÉ ROVNICE
část 4
EULEROVA KONSTANTA
část 5
ROVNICE A FUNKCE - a konkrétní veličiny v mechanice pohybu - rychlost, zrychlení, síla, výkon
část 2
integrální a diferenciální počet
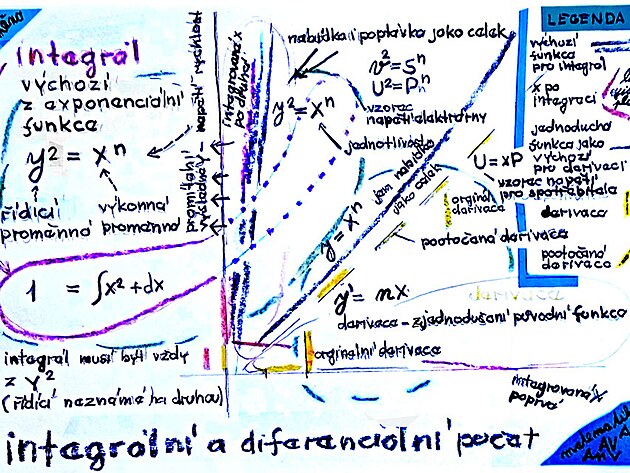
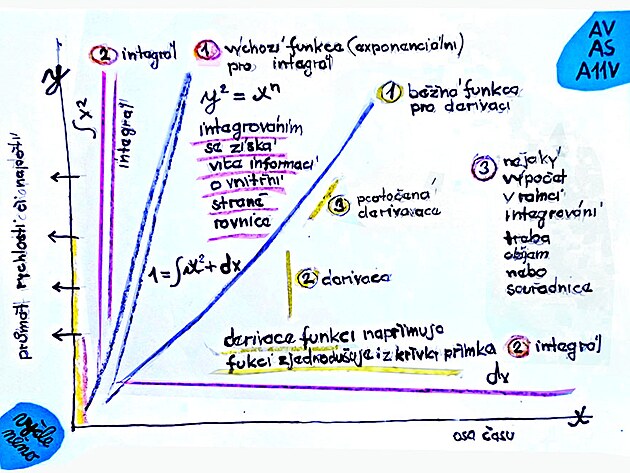
Pokud by se porovnal integrál - výchozí funkce - derivace - pak by mohl být na místě příměr "čajová plantáž" jako integrál, rostlina čaje jako výchozí funkce - a sáček z čajem jako derivace.
Čistě procesně - integrování a derivování se podobá - v obou případech se křivka nahrazuje úsečkou (která vychází z tečny k původní zkoumané funkce - a to ve tvaru křivky).
Zatímco v případě derivace se křivka zjednoduší - "obalí" - krátkými úsečkami - v případě integrování se původní křivka také zjednoduší - nahradí úsečkami - jenomže z lineární rovnice, či funkce se stane funkce vyššího řádu - která vychází z kvadratické rovnice - tedy se zvýší exponent z "na prvou" na exponent "na druhou" - tedy na místo jedné tečny - jako v případě derivace - tak v případě integrálu vlastně vznikne dvojice tečen - a mezi nimi plocha. Tuto plochu z boku vymezuje konstanta "c" - nazývaný také jako derivant (snad z důvodu, že integrování se procesně podobá derivování) - a tato kolmice - neboli rozteč integrálu vpodstatě prochází plochu integrálu z jednoho kraje na druhý - a na tomto principu funguje například zjišťování polohy vlaku.
Co je to vlastně vyjadřuje rovnice... Na vzdory rovnítka uprostřed neznamená, že levá a pravá strana rovnice vyjadřuje totéž.
LEVÁ STRANA (mohla by znamenat výsledek - řídící neznámou -, ale spíš vychází jako prostředek)
PRAVÁ STRANA rovnice obnáší nějaký pochod, FUNKCI, která zahrnuje skutečný VÝSLEDEK nějakého úsilí, výkonnou neznámou.
Řídící neznámá j- na levé straně rovnice - je zpravidla označována jako "Y" - výkonná neznámá zase jako "X" - dále v textu je poměrně často použito opačné označení - pro levou stranu "x" - pro pravou stranu "y".
Integrály nebo derivace nevytváří z původní funkce funkci vyššího ani nižšího řádu - pouze funkci upravují - aby se dalo zjistit například co daná funkce neumí (týká se to zejména integrálu) - nebo se funkce zjednodušila tak - aby se například neznámá vyskytovala nikoliv i v čitateli a zároveň jmenovateli zlomku - ale například jenom ve jmenovateli (v případě derivace).
Zjednodušeně lze shrnou - že derivace má podobný význam jako "Eulerova konstanta" - zatímco Eulerova konstanta zjednodušuje například trojúhelník na čtverec - derivace zjednodušuje parabolu na polopřímku. V kartézských souřadnicích také původní funkce i její derivace jsou umístěny přibližně ve stejných souřadnicích...
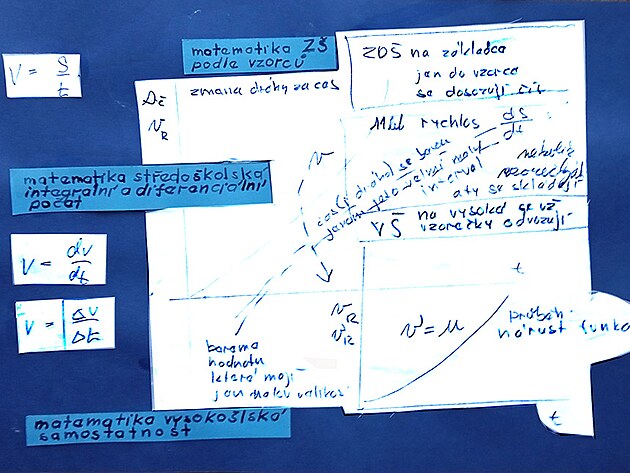
Například v případě definičního vzorce pro rychlost, tedy rychlost rovná se dráha lomeno čas, vlastním výsledkem je obvykle dráha (tedy přemístění z místa A do místa B( než rychlost - ta spíš vychází jako prostředek.
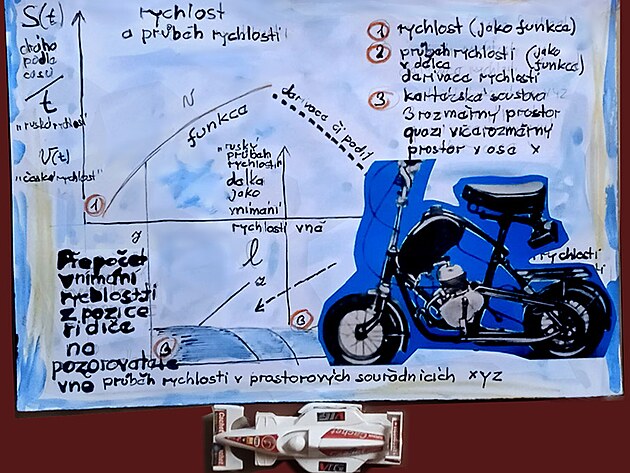
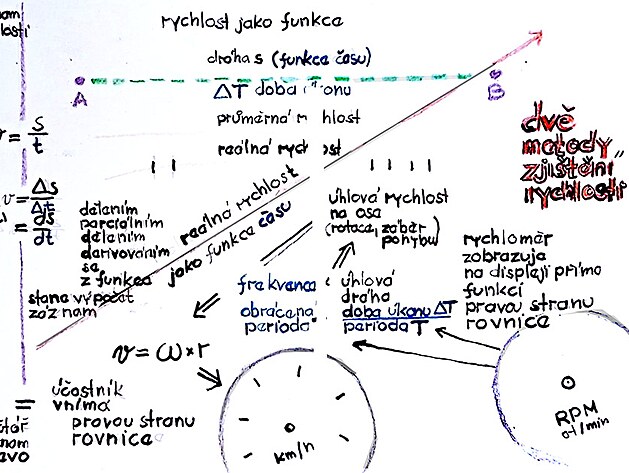
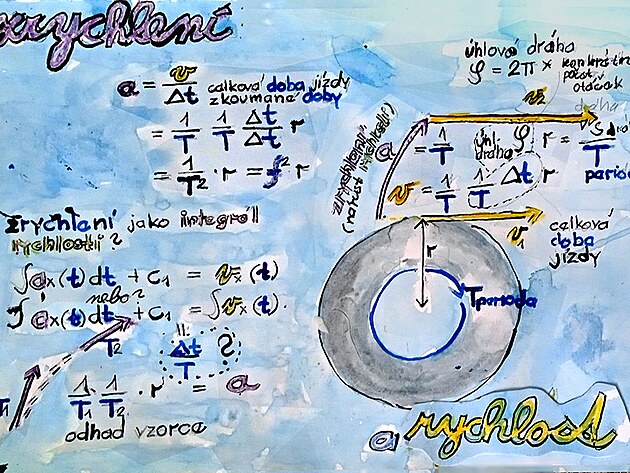
Na obrázku výše jsou jednak dvě metody zjišťování rychlosti (tedy jednak definiční metoda dráha lomeno čas, a druhá metoda přepočtem z frekvence,či otáček, na jaké jsou pravděpodobně založeny i měření rychlosti ve vozidlech.
Na výše uvedeném obrázku jsou ještě další informace a to pás vlevo, nazvaný jako záznam rychlosti - a plocha na pravo - která popisuje vlastní funkci pro výpočet rychlosti (nebo možná ještě přesněji - funkci pro uskutečnění například nějaké přepravy po stanovené dráze).
Vzhledem k faktu, že rychlost obvykle vytváří nějakou křivku - není zcela matematicky snadné vypočítat rychlost z celé dráhy, protože se rychlost různě liší...
Proto je pás vlevo označen jako záznam rychlosti, kde se liší jen různé metody výpočtu rychlosti (průměrná rychlost z celé dráhy a souhrnného času, parciální podíl, derivace). Derivace rychlosti neznamená nic jiného, než přesnější výpočet rychlosti než jinou metodou.
Derivaci, onomu symbolu doplněným čárkou, by v případě rychlosti spíš než označení derivace rychlosti lépe příslušelo označení výpočet rychlosti derivací.
diferenciální počet
Co je to vlastně derivace, případně integrál?
Jedním z mnoha vysvětlení by bylo, že derivace vlastně nepopisuje přesnou funkci, ale zjednodušuje ji na nárust funkce - nebo jak je například křivka v konkrétním místě strmá. Nebo také, že zjednodušuje křivku na přímku - s určitou orientací v kartézských souřadnicích.
V kartézských souřadnicích "x-y" je tedy funkce - de facto totéž jako její derivace - přibližně kolem mezi osy xy - jenom místo křivky - např.y = x na ntou -- třeba paraboly se vytvoří zjednodušená funkce y´ = n krát x , a například z krátkých úseček poskládaných z přímek derivací lze poskládat téměř původní funkci - její napodobeninu.
Derivováním se například z křivky vytvoří přímka (spíš úsečka) která se zobrazí do osy Y jako tzv. nárust funkce - následně se pootočí tak, že vytvoří tečnu původní křivky.
Z krátkých úseček - derivací funkce - se řekněme "obalí" původní funkce - a tím vznikne něco jako napodobenina původní funkce.
Rychlost je jedna funkce - a co se zjišťuje výpočtem – podobně jako se znázorňuje na osciloskopu jako napěti vlastně není napětí - ale nárust napětí (funkce "nárust napětí") - tedy v podstatě napětí vydělené časem/ - v případě vlaku z matematického hlediska nárust rychlosti - což je vlastně samostatná nárust rychlosti – a jednotlivých funkcí „nárust rychlosti“ by se vlastně měla dát poskládat reálná rychlost – čímž by se z definičního vzorce pro rychlost – dráho lomeno čas – měla dát poskládat průběh rychlosti podobně – jako přímým měřením rychlosti tachometrem – který ovšem funguje na jiném principu, a vychází z frekvence pohybu…
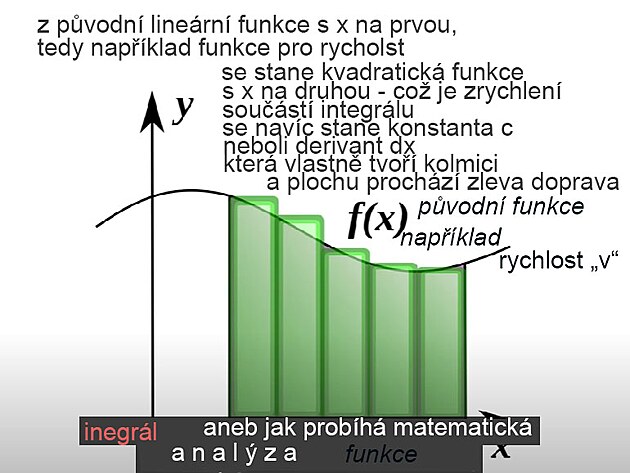
Integrál - zase do funkce začleňuje určitý přesah nějakého dalšího úkonu - řekněme do plochy přidává nějaký další rozměr. A takto integrál může podat informaci nejenom o rychlosti vlaku, ale i o jeho poloze...
integrální počet
Co se týče integrování - podle daných poznatků integrální počet vychází z kvadratické funkce pro řídící neznámou (tedy y na druhou) - na levé rovnice, a cílem integrování by podle všeho mělo být zjistit více informací a parametrů pro výkonnou neznámou na pravé straně rovnice.
V případě integrování se původní křivka zjednoduší podobně jako v případě derivace - nahradí úsečkami - jenomže z lineární rovnice, či funkce se stane funkce vyššího řádu - která vychází z kvadratické rovnice - tedy se zvýší exponent z "na prvou" na exponent "na druhou" - tedy na místo jedné tečny - jako v případě derivace - tak v případě integrálu vlastně vznikne dvojice tečen - a mezi nimi plocha. Tuto plochu z boku vymezuje konstanta "c" - nazývaný také jako derivant (snad z důvodu, že integrování se procesně podobá derivování) - a tato kolmice - neboli rozteč integrálu vpodstatě prochází plochu integrálu z jednoho kraje na druhý - a na tomto principu funguje například zjišťování polohy vlaku.
y na druhou (řídící neznámá) = x na n tou (výkonná neznámá)
Přičemž integrování je něco jako systém matematických operací, kterým se získává více informací o pravé straně rovnice s výkonnou neznámou (tedy X).
Levá strana rovnice s "Y" se nahradí hodnotou "1" ke které se srovnává pravá strana rovnice (v integrovaném tvaru).
Rovnicí o dvou řídících neznámých může být definováno například napětí z elektrárny do sítě - nastavené podle spotřeby - jednou by tatáž veličina "y" měla jakoby zastupovat zároveň prodejce a zároveň zákazníka.
Integrální počet by se ovšem měl zabývat pravou stanou rovnice - tedy výkonnou neznámou "x" - což v případě elektřiny buď může být buď výkon spotřebiče - nebo elektrický proud.
Integrál v zásadě zase není nic jiného než variace exponenciální funkce...
y na druhou = x na n tou
Co se týče integrování - podle daných poznatků integrální počet vychází z exponenciální funkce pro řídící neznámou (tedy y na druhou) - na levé rovnice, a cílem integrování by podle všeho mělo být zjistit více informací a parametrů pro výkonnou neznámou na pravé straně rovnice.
Rovnicí o dvou neznámých může být definováno například napětí z elektrárny do sítě - nastavené podle spotřeby - jednou by tatáž veličina "y" měla jakoby zastupovat zároveň prodejce a zároveň zákazníka.
Integrální počet by se ovšem měl zabývat pravou stanou rovnice - tedy výkonnou neznámou "x" - což v případě elektřiny buď může být buď výkon spotřebiče - nebo elektrický proud.
Integrováním by se mělo o pravé straně rovnice zjistit víc, než vychází z výchozí rovnice.
Integrování jakoby se pravá strana rovnice rozdělila na několik funkcí - přesněji řadu funkcí - od nejsložitější po nejjednodušší.
Integrováním jakoby se původní funkce z pravé strany rovnice - s jistým zjednodušením rozdělila například na x na druhou a na x na pravou.
A ze dvou jednodušších funkcí se dá zjistit více než z jedné funkce vyššího řádu. Dá se například vypočítat plocha - dají se například zjistit souřadnice.
OBSAH
část 1
ROVNICE A FUNKCE
část 2
INTEGRÁLY A DERIVACE
část 3
LOGARITMY a LOGARITMICKÉ ROVNICE
část 4
EULEROVA KONSTANTA
část 5
ROVNICE A FUNKCE - a konkrétní veličiny v mechanice pohybu - rychlost, zrychlení, síla, výkon
část 3 -logaritmus, logaritmování a logaritmické rovnice
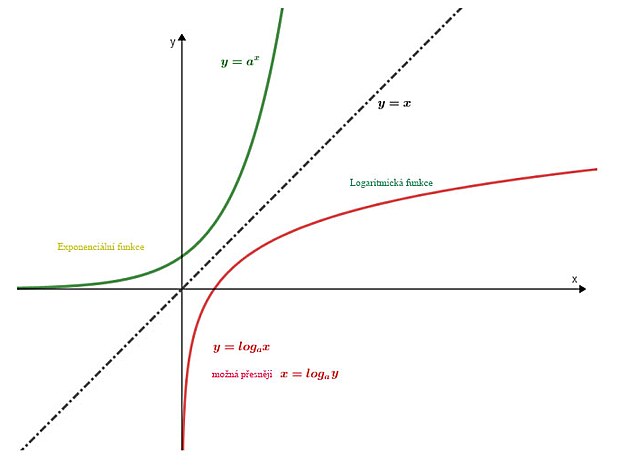
Logaritmus a logaritmování by mělo mít přibližně následující význam. Logaritmická funkce je vlastně doplňková funkce - pro nějakou obtížně řešitelnou matematickou funkci - a zjednodušuje výpočet - v mnoha případech původní funkci vůbec nejde běžnými matematickými nástroj vypočítat - a k výpočtu právě slouží logaritmus - který vlastně zjednoduší nejkomplikovanější složku původní funkce. Typickým případem logaritmování je výpočet exponenciální rovnice - u které je neznámá "x" v exponentu. V logaritmické rovnici se původní výkonná neznámá stane vlastně řídící neznámou.
Shrnuto - rovnice nebo funkce - které lze obtížně řešit standartním způsobem řešení rovnic - ted násobením, dělením - převáděním z jedné strany na druhou - tedy rovnice, které například výkonnou neznámou x obsahují v exponetntu - v sínu nebo cosínu - případně v nějakém jiném matematickém nástroji - tedy rovnice s touto komplikovaně začleněněnou neznámou - lze zjednodušit prostřednictvím logaritmické funkce - kde se vlastně z "X" stane řídící neznámá na levé straně rovnice - a lze vlastně tímto způsobem zpočítat. Kromě logaritmických rovnic se hodnoty z rozličných matematických nástrojů (mocniny, sinus, cosinus atd) - zejména dřív zpracovávaly prostřednictvím logaritmických tabulek - případě zjišťovaly prostřednictvím logaritmických pravítek - které obsahovaly několik stupnic s různými matematickými nástroji - přesnost výpočtů přes tabulky - případně pravítka byla pochopitelně méně přesná a zdlouhavější...
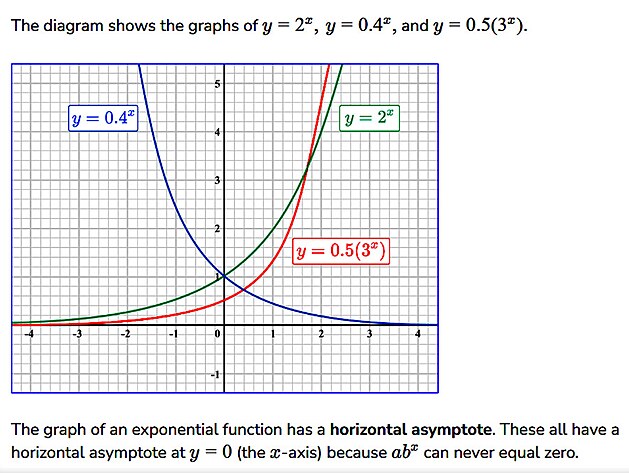
Vpodstatě lze konstatovat - k exponenciální rovnici je doplňkem logaritmická rovnice - čistě graficky je vlastně symetrická podle tečny k exponenciální rovnici - zatímco exponenciální se přimyká k ose y - logaritmická se přimyká k ose x. V případě funkce pro přirozený logaritmus je exponenciální a logaritmická rovnice symetrická i v rámci kartézských souřadnic.
Nejprve tedy k exponenciální rovnici. Kde se exponenciální rovnice vlastně uplatňuje? Na rozdíl od běžné rovnice například kvadratické kde se porovnává jedna neznámá s obdobnou neznámou - například napětí jako "y" s elektrickým proudem jako "x" na pravé straně rovnice - tak v případě exponenciální funkce proměnná na opačné straně rovnice nemůže být v základě - pokud zkoumaná veličina je ve své většině fixní. Například úbytek hmotnosti automobilu v důsledku spotřeby paliva.
Exponenciální rovnice by podle všeho být vlastně raketová rovnice - neboť hmotnost rakety je vpodstatě daná - a mění se jenom minimálně vzhledem k úbytku paliva, a tento úbytek paliva včetně úbytku hmotnosti by měl v jisté míře ovlivňovat i rychlost rakety...
Zde se vlastně jednalo o malou odbočku směrem k matematice kosmických letů - ale zpět hlavní téma příspěvku - což by měla být matematika rovnic, funkcí - integrálů a derivací...
Tečna exponenciální funkce je současně rovnicí (nebo funkcí) pro exponent, dá se konstatovat - že právě logaritmická funkce je rovnicí či funkcí pro výpočet exponentu.
Některá pravidla pro logaritmování...
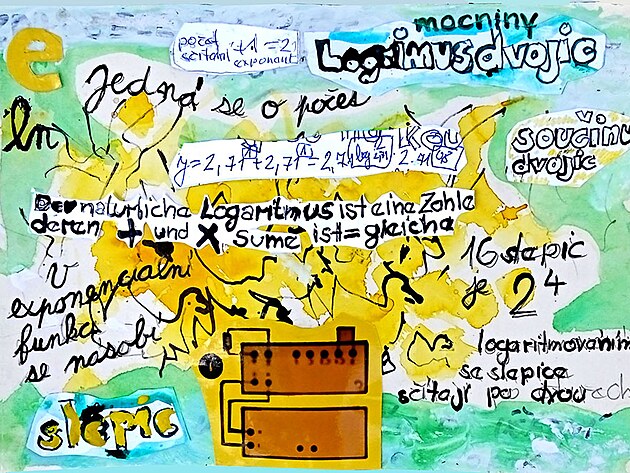
Například by pro logaritmus mělo platit - že logaritmus součinu je roven součtu logaritmů (což poněkud naznačuje i teze nastíněná výše - že logaritmus zjednodušuje výpočty - s jistými výhradami se například součin zjednodušuje na součet a tak dále.
Pravidlo že součin logaritmů odpovídá součtu logaritmů je také například nastíněno v ilustraci výše - podobenství o součtu dvojic slepic.
Stručně shrnuto - přostřednictvím logaritmické rovnice se vlastně zjišťuje či počítá exponent výchozí exponenciální rovnice s neznámou x v exponentu.
Graficky znázorněno - exponent této exponenciální rovnice je současně tečnou této exponenciální rovnice - a současně i tečnou doplňkové logaritmické rovnice. Logaritmická rovnice je vlastně funkcí pro nárust exponentu...
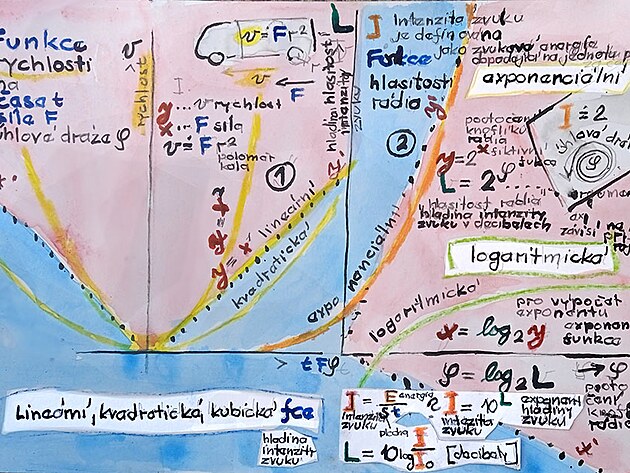
K ilustraci výše - pro zesilování zvuku rádia (y) jakoby platila exponenciální rovnice - kdy výkonná neznámá x v exponentu této rovnice řekněme zahrnovala čas kolikrát se musí pootočit knoflík rádia aby se dosáhl zvuk o určité hodnotě, Počítá se počet pootočení knoflíku rádia - a logaritmická rovnice je vlastně funkcí zvuku.
V případě logaritmické rovnice by navíc jakoby prohodila řídící neznámá y a výkonná neznámá x. Řídící neznámou se v případě logaritmické rovnice stane exponent "x" exponenciální rovnice. Takovou typickou exponenciální rovnicí by mohlo být například zesilování zvuku rádia - tedy relativně pozvolný začátek - pak jistý použitelný úsek pro zesílení zvuku - a následně zcela nepoužitelný úsek zvuku s velmi strmě se zesilující hlasitostí. Výkonnou neznámou "x" - původně v exponentu exponenciální rovnice by byl optimální čas k zesílení zvuku - nebo pootočení tlačítka - a řídící neznámou - tedy vlastně původní exponenciální funkcí by pak byla hlasitost rádia.
přirozený logaritmus
Průběh exponenciálních a logaritmických funkcí - zatímco číslo (tzv. argument) v exponentu zahrnuje nastavení přístroje - vlastní exponent "x" závisí podle uživatele - např. jak zesílí zvuk rádia - jak šlápne na plyn - přičemž argument - ke kterému se exponent vztahuje odvisí od konkrétního přístroje - například automobilu, rádia atd...
Mezi logaritmy - či logaritmickými rovnicemi mají vyjímečné postavení dekadický logaritmus - který odpovídá exponenciální rovnici o základu (argumentu) 10 a pak tzv. přirozený logaritmus - který odpovídá exponenciální rovnici - jejímž základem je Eulerova konstanta. Co se týče dekadického logaritmu - tak zřejmě vychází ze skutčnosti - že odpovídá zavedené desítkové soustavě. Co se týče přirozeného logaritmu - tak s velkou pravděpodobností vyjímečnost přirozeného logaritmu spočívá v přímé úměře mezi argumentem a exponentem exponenciální rovnice. Což se graficky projevuje symetrií mezi exponenciální funkcí a logaritmickou funkcí v kartézských souřadnicíc xy.
Přirozený logaritmus by měl být tedy funkcí pro kterou platí přímá úměra. Což naznačuje - že se přirozený logaritmus uplatňuje zejména ve statistice, ekonomice, teorie informací a inženýrství.
OBSAH
část 1
ROVNICE A FUNKCE
část 2
INTEGRÁLY A DERIVACE
část 3
LOGARITMY a LOGARITMICKÉ ROVNICE
část 4
EULEROVA KONSTANTA
část 5
ROVNICE A FUNKCE - a konkrétní veličiny v mechanice pohybu - rychlost, zrychlení, síla, výkon
část 4 -Eulerova konstanta
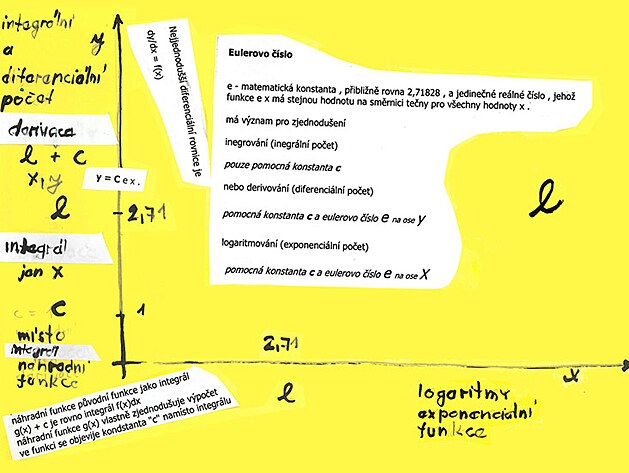
Leonhard Euler byl švýcarský matematik a fyzik 18. století, je po něm mino jiné pojmenováno Eulerovo číslo 2,7182818284.
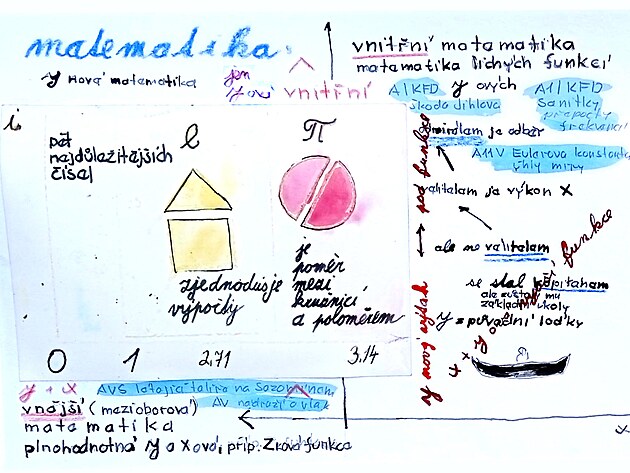
Eulerovo číslo patří mezi pět nejdůležitějších čísel v matematice. Pět nejdůležitějších čísel v matematice.
Eulerovo číslo - či konstanta - 2,71 má významů povícero. Například zjednodušuje výpočty. Například se prostřednictvím Eulerova čísla převádí trojúhelník na čtverec.
Dalším významem Eulerovy konstanty by měl spočívat - že se jedná o základ (argument) exponenciální rovnice s Eulerovým číslem - kde podle všeho platí přímá úměra mezi argumentem a exponentem této rovnice - a současně je v kartézské soustavě k této rovnici symetrická i logaritmická funkce - přesněji funkce přirozeného logaritmu - více výše zde v příspěvku.
Ludolfovo číslo "Pí" - zase vymezuje poměr mezi kružnicí a jejím poloměrem.
část 5 rozdíl mezi rovnicí a funkcí - průběh funkce - a přiřazení konkrétních funkcí z mechaniky pohybu (například rychlost, zrychlení, síla, výkon) k jednotlivým funkcím
Tato část příspěvku navazuje na část 1 - jenom jsou k obecným funkcím přiřazovány konkrétní funkce z mechaniky pohybu...
rychlost
Jako základní matematická funkce může být považována lineární funkce.
Zde uveden příklad y = 2x - 6
přičemž y může být označena jako řídící neznámý, x jako výkonná neznámá
Typickým příkladem lineární funkce může být vzorec pro rychlost...
Obecně známý vzorec pro rychlost je sice dráha lomeno čas - ale zde uveden vzorec
rychlost "v" = OMEGA (tzv. úhlová rychlost na ose hřídele) x r na druhou (r = poloměr kola)
ostatně OMEGA (úhlová rychlost lze rozčlenit na veličiny frekvence a úhlová dráha PSÍ) - a při vynásobení poloměrem kola by z úhlové dráhy vznikla běžná dráha, kterou například urazí vozidlo ...
přímo veličinou rychlost se ale podrobněji zabývají jiné příspěvky - rychlostí konkrétně zejména příspěvek Mechanika KFD 1 DAV - frekvence, rychlost, zrychlení / proč rychlé vozy mají velká kola - Blog iDNES.cz
zrychlení
Co se týče veličiny zrychlení - tak zrychlení se podobá veličině rychlost.
Zrychlení se od rychlosti liší především - nezahrnuje dráhu (a to ani úhlovou dráhu - která vychází z poštu otáček) - a je ještě jednou děleno časem (konkrétně periodou jedné otáčky "kola") - zrychlení je vpodstatě poloměr kola dělený dvakrát periodou otáčky - přičemž možná poněkud nepřesně lze jednu periodu považovat za výchozí - když se pohyb začne zrychlovat - a druhou periodu by bylo možno považovat za periodu - kdy se zrychlování například vozidla ukončí - a pohyb vozu se opět stane rovnoměrným.
síla
Veličina síla tvoří s veličinou rychlost něco jako dvojici příbuzných veličin - síla ovšem více vychází z hmotnosti břemene (rychlost jako by hmotnost zahrnovala pouze nepřímo) tedy síla například vychází z váhy automobilu - síla ovšem od rychlosti také liší - že není přesně periodizována časem jedné otáčky - síla vychází z různých matematických rovnic které by nějak měly zahrnovat váhu - například soustav rovníc - kdy jedna rovnice porovnává automobil před rozjezdem (vycházející z momentu setrvačnosti - který zahrnuje hmotnost automobilu) a automobil během jízdy (z momentu otáčení - která naopak zahrnuje veličinu síla). Síla je nadále ovlivněna zda se jedná o pohyb po rovině, nakloněné rovině - případně pád.
výpočty veličiny síla by se měl zabývat především příspěvek Matematická mechanika A0/ KFD 0 jak měří siloměr přes rychlost sílu / výpočty přes stopky - Blog iDNES.cz
výkon
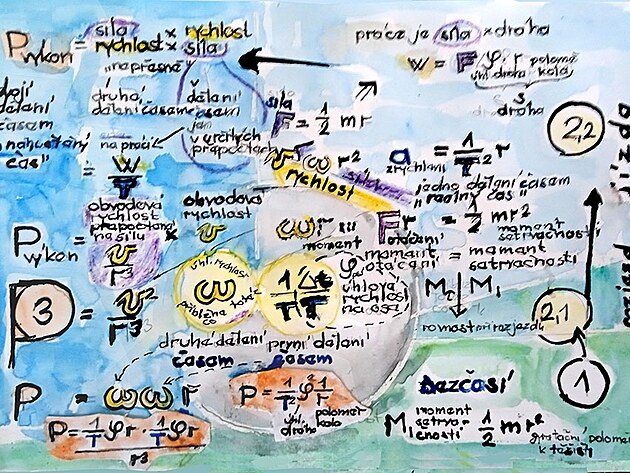
Souhrnnou veličinou v mechanice pohybu by byla veličina výkon. Výkon je vlastně momentem druhého stupně (ostatně momenty - jak moment setrvačnosti - tedy bezčasový moment nultého stupně - tak moment otáčení "Torque" - 1. stupně probíhající v reálném čase jsou poměrně nenázorné veličiny - spíš se jedná o matematickou funkci, či rovnici než o nějakou konkrétní veličinu - tedy výkon P jako moment 2. stupně lze vyjádřit vícerým způsobem - ale čím je výkon asi nejvíc typický - je, že se jedná o veličinu znovu - či podruhé dělenou časem - ovšem čas je ve veličině která se znovu dělí časem již jednou zahrnut. Výkon je tedy například "práce W" dělená dobou - neboli časem práce (jinak veličina "práce W" je v podstatě "síla F" vynásebená "dráhou s" - dráhu s lze zase přepočíst z "úhlové dráhy Psí" a vynásobit ji poloměrem kola r. Jinak je veličina "Výkon P" poměrně často popisována jako "rychlost v" krát "síla F" - což výkon sice poměrně vystihuje - ale není příliš přesné matematicky. Asi nejpřesnější by bylo výkon P definovat veličinou "úhlová rychlost OMEGA" na druhou x "poloměr r". Ostatně sídlem výkonu P jako by bylo rozmezí mezi osou a hřídelí a obvodem kola daným poloměrem "r". Ostatně dvojí násobení úhlovou rychlostí OMEGA jenom potvrzuje tvrzení o dvojím dělení časem. Dvojí dělení časem je sice možno také zjistit u veličiny "zrychlení a" - ale v případě zrychlení jde vlastně o dvojí čas na jeden úkon - z čehož jeden z těchto časů lze přičíst právě změně - kterou představuje zryhlení. V případě výkonu je věc jiná. Jeden úkon jakoby se porovnával s časem dvakrát. Například již hotová veličina práce W se znovu dělí časem. Veličina práce W je veličina síla F přenásobená dráhou s. Z hlediska mechaniky pohybu je ovšem než veličina síla F asi snadněji vymezitelná veličina "rychlost v" - jelikož výpočty a přepočty veličin "rychlost" a "čas" jsou vymezeny podstatně jednoznačněji než přepočty síla a čas - síla je spíš pohybovou variací hmotnosti než variací času... Pokud by se pro výpočet veličiny "výkon P" - vycházelo z teze výkon přiblžně odpovídá rychlost a síla - pak by přepočet výkonu jenom přes rychlost vycházel asi následovně...
Výkon P z obvodové rychlosti = "v rot" (jako rychlost) x (rychlost přepočtená na sílu)"v rot" /lomeno poloměr na třetí
Výkon P z úhlové ryhlosti OMEGA na hřídeli = OMEGA na druhou x "poloměr r" (při přepočtech úholové rychlosti OMEGA na obvodovou rychlost "v" podle vzorce "OMEGA" = V /lomeno "r na druhou" - by vyšel ten samý vzorec jak uvedeno výše...
Jan Tomášek
Dálniční most přes Křešické údolí 3 - kinematika stavebních strojů a stavba mostů

Příspěvek by se měl zabývat především oborem zvaný kinematika - což je poměrně důležitý předmět ve stavebnictví a strojírenství - i když na rozdíl od statiky nebo dynamiky - nepřináší výsledky v cifrách - ale spíše jenom analyzuje
Jan Tomášek
Kamna na piliny - "piliňák"

Kamna na piliny mohou být součástí stolařských dílen, nebo provozoven kde se hodně brousí, hobluje - vznikají piliny a hobliny a mohou sloužit třeba k běžnému topení.
Jan Tomášek
Sněhový pluh KSP 411 / LPO 411 S - užitková železniční vozidla, uhlí a důlní lokomotivy
Když zasněží, a trať se stane skrze závěje nesjízdnou neznamená, že by vlaky vůbec neměly vyjet. Ve větších železničních stanicích jsou zpravidla pro tento účel k dispozici různá speciální železniční vozidla - třeba sněhové pluhy.
Jan Tomášek
Cesty energie 2E - jak platit za elektřinu QR kódem, elektřina, plyn a ekonomika, HE Most

Příspěvek by měl pojednávat především o administrativě a ekonomice - především z hlediska spotřebitele - jak se za elektřinu vlastně platí. Ekonomika by měla být pojednána rovněž z hlediska výroby a distribuce.
Jan Tomášek
Mechanika KFD 1 DAV - frekvence, rychlost, zrychlení / proč rychlé vozy mají velká kola
Dva obory mechaniky pohybu - kinematika a dynamika - dá se říci odlišuje právě frekvence a rychlost - tedy od zvuků periody, přes frekvenci a pootočení - dále přes rychlost úhlovou, rotační až po lineární rychlost, atlas Škoda.
| Další články autora |
Studentky rozrušila přednáška psycholožky, tři dívky skončily v nemocnici
Na kutnohorské střední škole zasahovali záchranáři kvůli skupině rozrušených studentek. Dívky...
Tři roky vězení. Soud Ferimu potvrdil trest za znásilnění, odvolání zamítl
Městský soud v Praze potvrdil tříletý trest bývalému poslanci Dominiku Ferimu. Za znásilnění a...
Podvod století za 2,4 miliardy. Ortinskému hrozí osm let a peněžitý trest 25 milionů
Luxusní auta, zlaté cihly, diamanty a drahé nemovitosti. To vše si kupoval osmadvacetiletý Jakub...
Rusové hlásí průlom fronty. Ukrajinská minela jim přihrála klíčové město
Premium Jako „den průlomů“ oslavují ruští vojenští blogeři pondělní události na doněcké frontě, kde se...
NATO by Rusy porazilo, Putin má jedinou naději, řekl polský ministr zahraničí
Rusko by se mělo bát Severoatlantické aliance, protože ho v případě střetu s ní čeká „nevyhnutelná...
Riziko požárů platí až do čtvrtka. Pálení čarodějnic zkomplikuje i vítr
Český hydrometeorologický ústav (ČHMÚ) prodloužil výstrahu varující před nebezpečím vzniku požárů...
Kandidát na ministra za TOP 09 Tuleja vedl univerzitu, dohlíží i na OKD
Novým ministrem pro vědu, výzkum a inovace se má stát Pavel Tuleja, který ve vládě nahradí Helenu...
Rusové při smrtícím útoku na Oděsu zničili i „zámek Harryho Pottera“
Sledujeme online Na pět vzrostl počet obětí pondělního ruského útoku na jihoukrajinskou Oděsu, jeden ze 32 zraněných...
Předsednictvo TOP 09 podpořilo Tuleju. Pozice ve vládě ho zajímá
Novým ministrem pro vědu, výzkum a inovace se má stát prorektor Slezské univerzity v Opavě pro...

PRACOVNÍK PODPORY PRODEJE (A12500)
AURES Holdings a.s.
Olomoucký kraj
nabízený plat:
30 000 - 32 000 Kč
- Počet článků 192
- Celková karma 0
- Průměrná čtenost 1043x