Všechny fraktály, které jsme až dosud viděli, vznikly z opakovaného dosazování do kvadratické rovnice ve dvou proměnných. V mysli zvídavého čtenáře by tak měla vytanout otázka, co je na kvadratické rovnici (jejíž přesný tvar byl popsán v prvním dílu) tak magického, že dokáže v rovině vytvořit takové jemné až esoterické obrazce.
Odpověď na tuto otázku je celkem jednoduchá. Na kvadratické rovnici není speciálního vůbec nic. To bohatství tvarů je způsobeno nelinearitou té rovnice a kvadratická funkce je prostě ze všech nelinearit ta nejjednodušší. Jiná nelineární - řekněme kubická - rovnice by dokázala vytvořit podobně pohádkové obrazce.
Dřív než se na pár takových podíváme, chtěl bych se na chvíli zastavit u hluboké propasti, která se táhne napříč celou matematikou. U propasti, která odděluje lineární a nelineární jevy.
Zhruba řečeno - a nebude to matematicky úplně přesný popis - lineární objekty jsou takové, které obsahují proměnné pouze v jejich nejjednodušší formě, což znamená v první mocnině. Například výrazy jako 1+x, 3-2x+y, x-2y+11z jsou lineární. Na druhé straně výrazy jako x2+y2, xy-2, a3+b3-c5 jsou nelineární protože obsahují proměnné ve vyšších mocninách (výraz xy je násobkem dvou proměnných, díváme se na něj tedy jako na člen kvadratický).
To, že analýza lineárních objektů je podstatně jednodušší jste asi zjistili už na střední škole. Zatímco řešení lineární rovnice (třeba 2x+1=3) se dá udělat prakticky "z ruky", na vyřešení rovnice kvadratické budete potřebovat poměrně komplikovanou formulku a na kubickou rovnici už si budete muset zavolat "řemesníka" (zeptejte se strýčka Googla na "Cardanovy vzorce" pokud Vás to zajímá). U soustav rovnic je tento rozdíl ještě markantnější. Zatímco lineární soustavy rovnic o více proměnných se stále dají vyřešit na úrovni střední školy, u soustav nelineárních si většinou musíte vypomoci s numerickými metodami (tedy když to řeknu česky, musíte zapřáhnout počítač).
Hezky je ta propast vidět také u dynamických systémů - tedy fyzikálních, biologických či jiných jevů, jejichž vývoj v čase se dá popsat nějakou matematickou formulkou. U lineárních systémů se dá chování v čase opět poměrně přesně spočítat a stacionární stavy takového systému a jejich stabilita se dají odvodit analyticky. Nelineární systémy se chovají podstatně záludněji a v podstatě se dá říci, že celá slavná teorie chaosu je vlastně jen analýzou nelineárních dynamických systémů.
Ale nemusíme se trmácet tak daleko do hlubin matematické džungle. Ta propast mezi lineárním a nelineárním světem je patrná i u objektů nejjednodušších - u přirozených čísel (tedy 1,2,3,4,5,6,7,...).
Jak si jistě vzpomínáte, přirozená čísla se v zásadě dělí na čísla složená - ta se dají napsat jako součin menších faktorů (třeba 15=3*5, 49=7*7 nebo 120=23*3*5) - a na prvočísla, která nerozložíte na faktory ani kdybyste si sundali kravatu (například 11, 29 nebo 83). Už od dob Euklidových víme, že prvočísel je mezi přirozenými čísly nekonečně mnoho.
Co když si ale vezmeme pouze menší posloupnost čísel, kterou dostaneme třeba tak, že začneme s 11 a budeme postupně přičítat řekněme 10: 11,21,31,41,51,61,71,...? Matematicky se tato posloupnost dá zapsat lineární formulkou 1+10x (kde za x dosazujeme přirozená čísla). Vidíte sami, že některá čísla jsou složená (21 a 51) a jiná jsou prvočísla (třeba 11 a 71). Bude ale těch prvočísel stále nekonečně mnoho? Nebo si vezměme jinou formulku, 2+3x, tedy začneme s 5 a budeme postupně přičítat 3: 5,8,11,14,17,20,23... Opět vidíte, že některá čísla jsou složená a některá jsou prvočísla. Ale zda je těch prvočísel nekonečně mnoho není na první pohled vidět.
No, nebudu Vás dlouho napínat. Už v roce 1837 zjistil německý matematik Dirichlet, že všechny posloupnosti, které se dají popsat (netriviální) lineární formulkou musí obsahovat nekonečně mnoho prvočísel. Jedna každá z nich. A jak je to tedy s nelineárními posloupnostmi? Z těch jsou asi nejjednodušší posloupnosti kvadratické a z nich je zase nejjednodušší posloupnost daná formulkou x2+1 (tedy umocnit přirozená čísla na druhou a přičíst 1). Prvních pár členů této posloupnosti vypadá takto: 2,5,10,17,26,37,50,65,82,101,... Opět vidíme, že některá čísla jsou složená a jiná jsou prvočísla. Ale bude těch prvočísel nekonečně mnoho?
Odpověď na tuto otázku je, že nevíme. Nejen, že to nevím já nebo že to neví Váš matykář na vysoké škole - ale nikdo to neví. Nikdo na celém široširém světě. To jsou poměry, co? My si tady na Zemi klidně štěpíme atom, posíláme kdejakého čokla do vesmíru, ale pořád nevíme, zda ta nejjednodušší kvadratická posloupnost obsahuje nekonečně mnoho prvočísel. Už to vám dává představu jak tajuplný svět nelinearit je. A fraktály jsou toho živoucím důkazem.
Tím máme matyku z krku a teď zase nějaké obrázky.
V dnešním vydání tedy nahradím kvadratickou rovnici nějakou komplikovanější nelinearitou a podíváme se jak bude vypadat příslušná Mandelbrotova množina (zkoumání příslušné Juliovy množiny nechám na příště). A aby nebyl zápis moc komplikovaný, budu používat komplexní proměnnou z (pokud nevíte co to je, nelamte si s tím hlavu - na téhle úrovni to nehraje roli). Důležitý je charakter té nelinearity - tedy zda je kvadratická, kubická a nebo maková. Ta formulka v původní Mandelbrotově množině by se tedy dala zapsat jako f(z)=z2.
Pro každou formulku ukážu nejdříve celou Mandelbrotovu množinu a pak se vydáme do jejích hlubin prostřednictvím navigačních čtverečků - každý obrázek (kromě posledního v každé sérii) obsahuje malý čtvereček a následující obrázek je vždy zvětšením toho čtverečku. Obvykle ukážu dvě až tři zvětšení.
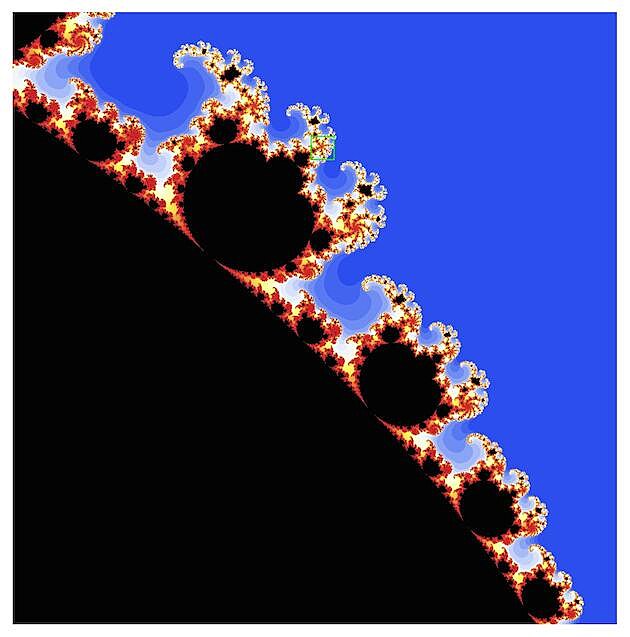
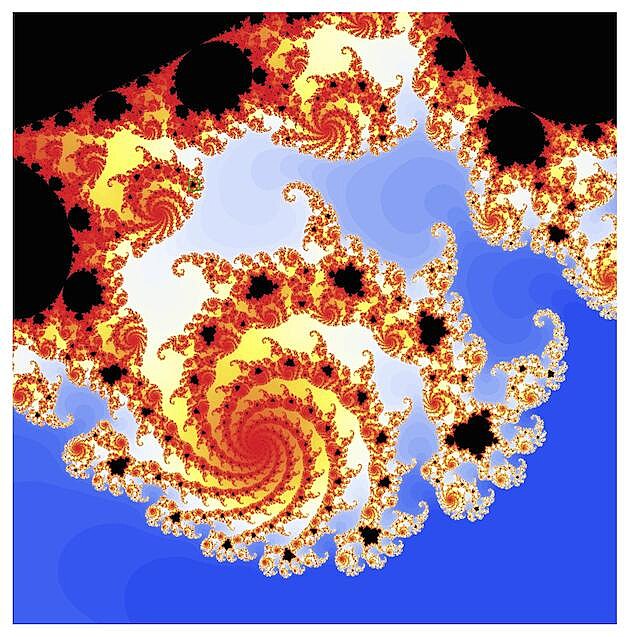
1. f(z)=z3
První výlet do oblasti vyšších nelinearit nás zavede k funkci kubické (tedy třetí mocnina). Všimněte si, že výsledná Mandelbrotova množina vypadá tak trochu jako slepenec (dvojlístek) dvou kopií originální množiny diskutované v prvním vydání.
(tady musím trochu šoupnout barevnou škálu - čtvereček je v horní prostřední části)
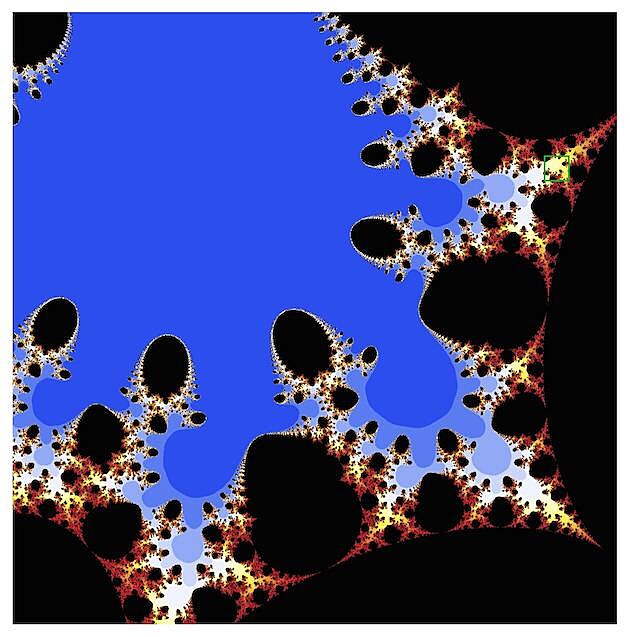
2. f(z) = z4
Druhé zastavení bude patřit funkci bikvadratické (tedy čtvrté mocnině). Tahle vypadá tak trochu jako trojlístek vytvořený původní množinou. Tipne si někdo, jak bude vypadat pátá mocnina?
(teď měním barvu výřezových čtverečků na zelenou - tady je uprostřed té severní cibulky)
3. f(z) = z5
Pátá mocnina - improvizovaný čtyřlístek.
(další výřezový čtvereček není moc vidět - je na spodu levé severní cibulky)
(a tady je zhruba 2 cm od levého kraje a 2 cm od vrchního)
4. f(z) = z9
Teď už tu hru celkem známe a tak se mrkneme rovnou na devátou mocninu a tedy osmilístek.
5. f(z) = z99
Možná jste si všimli, že ten předchozí fraktál není tak výrazý jako ty předchozí a barvy se trochu míchají. To je proto, že čím vyšší mocninu si vezmete, tím rychleji čísla, která dosazujete, rostou a v jistém okamžiku začne mít počítač (konečný to tvor) problémy s rozlišením. Viz následující 99. mocnina. Vyjde z toho sice asi 98 lístek (ty čudlíky jsem nepočítal, ale věřím, že jich je 98), nicméně při zvětšení čtverečku uvidíme, že výsledný fraktál je takový rozháraný a počítač už má problémy to iterativní schéma z hlediska přesnosti ukočírovat.
6. f(z) = z3 + z2 - 2*z + 1
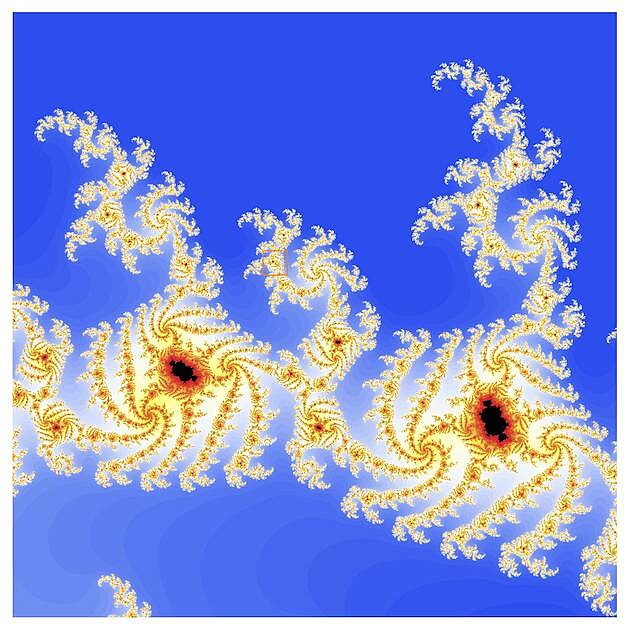
A abychom rozloučili něčím hezkým, vrátíme se ke kubické funkci, ale trochu si ji pozměníme (pro znalce: tento polynom má jeden reálný a dva komplexní kořeny). Ze začátku ta Mandelbrotova množina sice také nevypadá valně, ale když budete chvíli hledat, najdete v ní krásnou zátoku s mořskými koníky.
A to je pro dnešek vše.
Některé fraktály ve větším rozlišení najdete zde.
