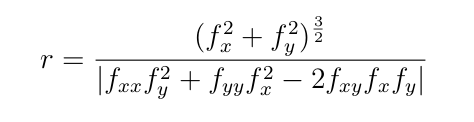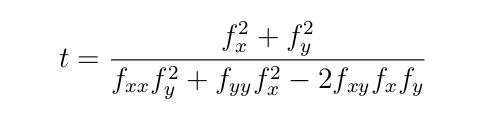Nedávno jsem do jednoho programu potřeboval počítat poloměr křivosti i křivky dané implicitně. Slídil jsem po netu, ale kýžený vzorec jsem nenalezl. Musel jsem ho odvodit a tak si ho sem pro jistotu zapíšu, kdybych to ještě někdy potřeboval.
Nechť je dána křivka implicitně rovnicí f(x, y) = 0, kde f je funkce spojitá v obou proměnných x a y má spojité derivace až do řádu 2. Pak poloměr křivosti r v bodě křivky (x, y) je dán vzorcem:
kde fx a fy značí parciální derivace vzhledem k x a y. fxx, fyy a fxy jsou parciální derivace druhého řádu.
Pokud navíc označíme:
pak pro střed křivosti s platí:
Důkaz není těžký, je jen trochu dlouhý a psát ho tady v html asi nemá cenu. Můžeme ale zkusit příklad.
Najděte poloměry křivosti elipsy (x/a)2 + (y/b)2 = 1 v bodech (a, 0) a (0, b). Parciální derivace jsou:
fx = 2x/a2
fy = 2y/b2
fxx = 2/a2
fyy = 2/b2
fxy = 0
Pro r pak platí:
r = (4((x/a2)2 + (y/b2)2))3/2/(8((x/a)2 + (y/b)2)/(ab)2)
Výraz ve jmenovateli za "osmičkou" je ovšem z definice elipsy roven jedné, tedy:
r = (ab)2((x/a2)2 + (y/b2)2)3/2
Pro bod (a, 0) je tedy poloměr roven b2/a, pro bod (0, b) je roven a2/b. Pro a = b = R, tedy pro kruh o poloměru R je poloměr křivost v obou bodech roven R.
Obdobným způsobem můžeme spočítat t:
t = (ab)2((x/a2)2 + (y/b2)2)/2
A dosadíme-li do vzorců pro souřadnice středu křivosti, dostaneme po krátké úpravě:
sx = x3(a2 - b2)/a4
sy = -y3(a2 - b2)/b4
Vynásobíme-li sx áčkem, sy béčkem a umocníme-li oba výrazy na 2/3, dostaneme:
(asx)2/3 + (bsy)2/3 = (a2 - b2)2/3
což je známá rovnice zobecněné asteroidy, kterážto je evolutou elipsy. Tak to asi platí.
