Cesta do hlubin fraktálovy duše VIII

V dnešním pokračování fraktálové série se na jemně tepané matematické krajkoviny podíváme pohledem dynamických systémů. Pro prakticky zaměřené estéty pak v druhé části vybalím spoustu oku lahodících obrázků.

Minule jsme se podívali, jak se Mandelbrotova množina chová pro komplikovanější komplexní funkce. Dnes se vrátíme k množině Juliově a podíváme se na ni prizmatem dynamických systémů.

Diskretní dynamický systém je v podstatě funkční iterace - tedy opakované dosazení do nějaké formulky. Vybereme si vhodnou nelineární funkci, dosadíme do ní a to, co nám vyjde, dosadíme zpátky do funkce (jako další iteraci). A tento proces neustále opakujeme.

Jako nejjednodušší příklad si vezměme funkci f(x) = x2.

Abychom mohli iteraci nastartovat, budeme ještě potřebovat počáteční hodnotu x0 - tedy číslo, které do funkce dosadíme jako první (všechna další čísla, která nám budou během iterace z funkce "vypadávat" už jsou touto libovolně zvolenou hodnotou plně určena).

Iterací tedy dostaneme posloupnost čísel, které budu říkat orbita (dané počáteční hodnoty x0). Z pohledu fraktálů budeme rozlišovat orbity, které se nikdy příliš nevzdálí od počátku (typ A) a orbity, které dříve nebo později odběhnou do nekonečna (typ B). Tady je příklad toho iterativního dosazování do funkce f(x) pro x0=1, resp. x0=3

(typ A) 1 › 1 › 1 › 1 › 1 › 1 › ....

(typ B) 3 › 9 › 81 › 6561 › 43046721 › 1853020188851841 › ...

Kdy si to rozmyslíte, zjistíte, že pro tuto konkretní funkci x2 vedou počáteční podmínky mezi -1 a 1 k orbitám typu A, zatímco všechny ostatní vedou k typu B. Na reálné ose bychom ale moc krásy nenalezli, takže pro potřeby fraktálů budeme iterovat komplexní funkce. Pokud si v komplexní rovině obarvíme (počáteční) body vedoucí k orbitě typu A černě a ty, které vedou k orbitě typu B, barevně (kde tón barvy bude odpovídat počtu iterací, potřebných k tomu, abychom se dostatečně vzdálili od počátku), dostaneme obrázek tzv. Juliovy množiny (viz Galerie níže).

Abychom se ale mohli podívat, co se při výpočtu fraktálů děje pod kapotou, podíváme se na pár orbit zblízka (tyto obrázky jsou ale pouhým mezivýpočtem a v konečném fraktálu je neuvidíte).

Na obrázku vpravo jsem si vzal posunutou kubickou funkci f(z)=z3+s (kde s je pevně zvolený komplexní parametr) a sestrojil orbitu odpovídající počáteční hodnotě z0 = 0.2+0.4i (červený bod). Abychom lépe viděli dynamiku této orbity, měním s průběhem času barvu od tmavě zelené po žlutou (v daném případě se orbita spirálovitě propadá dovnitř, skáče z jedné větve "galaxie" na druhou, ale při tom zůstává v naznačených mezích, takže se jedná o typ A).

Z pohledu dynamiky má každá orbita v komplexní rovině spoustu možností, jak se příliš nevzdálit od počátku - může se blížit k nějakému ekvilibriu, může se namotat na periodickou orbitu a nebo může v okolí počátku jen tak chaoticky hopsat. Fraktálům je ovšem jedno, co orbita přesně provádí - pro všechny tyto možnosti je nakonec připravena černá barva. Důležité je, aby neodběhla k nekonečnu. Ve výsledném fraktálu by tedy bod z0 = 0.2+0.4i byl vyznačen černě. Tu orbitu samotnou v něm neuvidíte. Její charakter pouze určí barvu v dané počáteční podmínce (de facto ten červený bod "přesadíme" do fraktálu, udělíme mu barvu odpovídající typu té iterační orbity, a vezmeme si další počáteční hodnotu ke zkoumání).

Souhrnně pak tyto body tvoří Juliovu množinu funkce f. Její obrázek je tak de facto mapou chování orbit pro různé počáteční hodnoty (každý pixel odpovídá jednomu komplexnímu číslu, a tedy jedné počáteční hodnotě). A jak jsme si už řekli - komplexní čísla nalézající se v černé části množiny vedou k orbitám typu A.

Abychom viděli, jak může orbita z okolí počátku uniknout, podívejme se na obrázek vlevo (orbita červeného bodu opět běží od tmavě zelené do žluté). Po několika "nerozhodných" úvodních iteracích se orbita dostane do bodu vpravo dole a odtud pak už nezadržitelně odběhne do nekonečna. To znamená že v konečném fraktálu by tento počáteční červený bod získal nějaký nečerný odstín (podle zvoleného barevného schematu a rychlosti "odběhnutí").

Samozřejmě z okolí počátku se dá "dynamicky" uniknout i jinak - například po spirále, jako v obrázku předchozím, jen s tím rozdílem, že ta spirála se tentokrát bude kroutit směrem "ven".

V jistém smyslu tedy barvy na obrázku Juliovy množiny indikují stabilitu (zhruba řečeno - stabilní objekty přitahují okolní orbity, zatímco nestabilní je odpuzují - nezřídka až do nekonečna). V již zmíněném dynamickém Matykání jsme viděli, že pokud objekt ztratí stabilitu (změnou parametru), tak v tom prvním okamžiku ještě odpudivé síly nejsou dostatečně silné a body v jeho okolí si tu stabilní orbitu "pamatují", takže než se definitivně vzdálí, chvíli se potloukají v jeho blízkosti (jako na tom obrázku vlevo). A tohle zpomalení "úniku" má za následek, že k "dosažení nekonečna" potřebují orbity o něco delší čas než orbity "nezpomalené" (třeba z toho úvodního celočíselného příkladu) a to se ve fraktálním obrázku projeví změnou tónu barvy. V závěrečné sekci dnešní galerie je několik ukázek tohoto fenoménu. Ta černá množina už tam není (pro všechny počáteční podmínky odběhnou orbity do nekonečna), ale oblasti se "zpomalenou dynamikou" stále dokážou vytvořit podivuhodně jemné obrazce.

+++++++++

Galerie

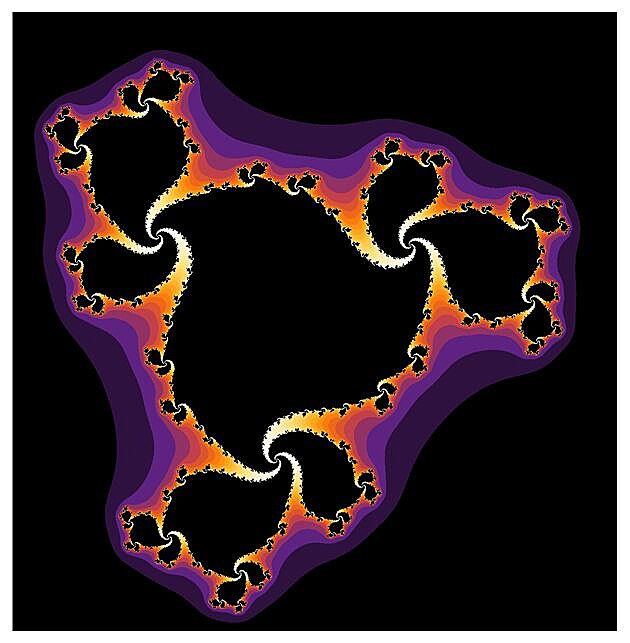
Všechny obrázky Juliových množin níže vznikly iterací kubické funkce f(z)=z3+s, pro nějaké pevně zvolené komplexní číslo s. To mimochodem znamená, že všechna ta krása a mnohovrstevnost každého obrázku je plně zakódována v jednom jediném komplexním čísle s. Začneme s hodnotami s uprostřed Mandelbrotovy množiny, kde je ta černá, stabilní část poměrně robustní.

+++++++++

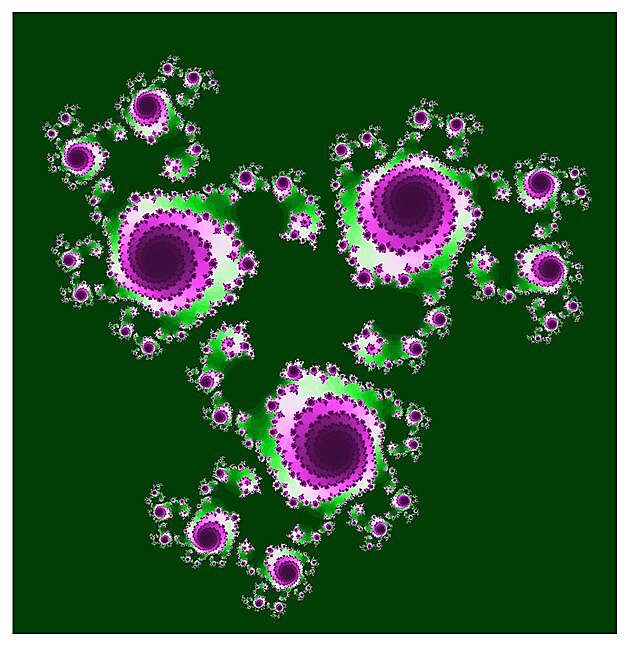
V okamžiku kdy se s hodnotou s začneme blížit k hranici Mandelbrotovy množiny, tak se ta černá část Juliovy množiny začne postupně ztenčovat, drobit a rozsypávat.

+++++++++

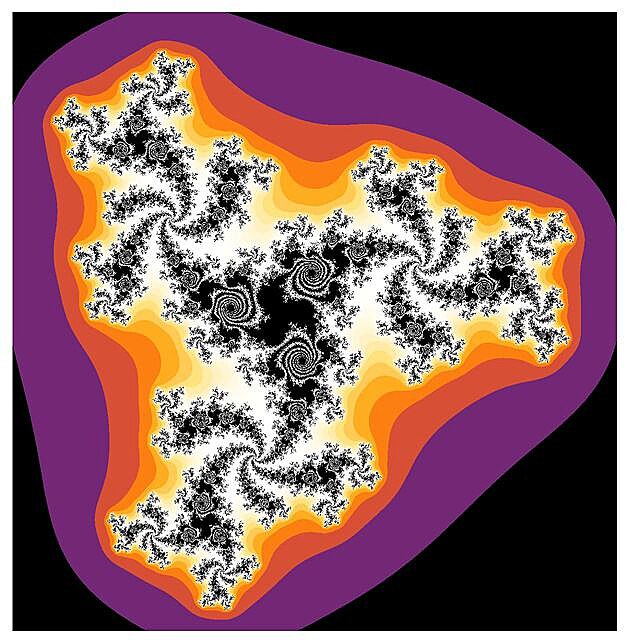
A když se s parametrem s dostaneme mimo Mandelbrotovu množinu, ty černé oblasti zmizí úplně, protože všechny orbity (z jakékoliv počáteční komplexní hodnoty) uniknou do nekonečna. Nicméně pokud jste stále dostatečně blízko její hranici (tentokrát zvnějšku), tak ten zpomalovací efekt popsaný na konci textu stále dokáže vymalovat celou řadu zajímavých obrázků.

+++++++++

Předchozí díly série "Cesta do hlubin fraktálovy duše"